Difference between revisions of "Contact surgery"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (AUTOMATIC EDIT (latexlist): Replaced 60 formulas out of 65 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 65 formulas, 60 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | A special type of [[Surgery|surgery]] on a (strict) contact manifold $( M ^ { 2 n - 1 } , \xi )$ (i.e. a smooth manifold admitting a (strict) contact structure $\xi = \operatorname{ker} \alpha$, where $\alpha$ is a $1$-form satisfying $\alpha \wedge ( d \alpha ) ^ { n - 1 } \neq 0$), which results in a new contact manifold. | ||
| − | + | In topological terms, surgery on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120200/c1202006.png"/> denotes the replacement of an embedded copy of $S ^ { k } \times D ^ { m - k }$, a tubular neighbourhood of an embedded $k$-sphere with trivial normal bundle, by a copy of $D ^ { k + 1 } \times S ^ { m - k - 1 }$, with the obvious identification along the boundary $S ^ { k } \times S ^ { m - k - 1 }$. Alternatively, one can attach a $( k + 1 )$-handle $D ^ { k + 1 } \times D ^ { m - k }$ along $S ^ { k } \times D ^ { m - k }$ to a manifold $W ^ { m + 1 }$ with boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120200/c12020015.png"/>, and the new boundary will be the result of performing surgery on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120200/c12020016.png"/>. | |
| − | + | As shown by Y. Eliashberg [[#References|[a2]]] and A. Weinstein [[#References|[a11]]], contact surgery is possible along spheres which are isotropic submanifolds (cf. also [[Ising model|Isotropic submanifold]]) of $( M , \xi )$ and have trivial normal bundle. The choice of framing, i.e. trivialization of the normal bundle, for which contact surgery is possible is restricted. | |
| − | + | A contact manifold $( M , \xi = \operatorname { ker } \alpha )$ may be regarded as the strictly pseudo-convex boundary of an almost-complex (in fact, symplectic) manifold $W = ( M \times ( 0,1 ] , J )$ such that $\xi $ is given by the $J$-invariant subspace of the tangent bundle $T M$. Contact surgery on $M$ can then be interpreted as the attaching of an almost-complex or symplectic handle to $W$ along $M$, and the framing condition for $n > 2$ is given by requiring the almost-complex structure on $W$ to extend over the handle. For $n = 2$ the situation is more subtle, see [[#References|[a2]]], [[#References|[a5]]]. Weinstein formulates his construction in terms of symplectic handle-bodies, Eliashberg (whose results are somewhat stronger) in terms of $J$-convex Morse functions on almost-complex manifolds (cf. also [[Almost-complex structure|Almost-complex structure]]; [[Morse function|Morse function]]). | |
| − | + | A [[Stein manifold|Stein manifold]] of real dimension $2 n$ has the homotopy type of an $n$-dimensional [[CW-complex|CW-complex]], cf. [[#References|[a8]]], p. 39. Eliashberg uses his construction to show that for $n > 2$ this is indeed the only topological restriction on a Stein manifold, that is, if $W$ is a $2 n$-dimensional smooth manifold with an almost-complex structure $J$ and a proper Morse function $\varphi$ with critical points of Morse index at most $n$, then $J$ is homotopic to a genuine complex structure $J ^ { \prime }$ such that $\varphi$ is $J ^ { \prime }$-convex and, in particular, $( W , J ^ { \prime } )$ is Stein. | |
| − | + | The usefulness of contact surgery in this and other applications rests on the fact that there is an [[H-principle|$h$-principle]] for isotropic spheres. This allows one to replace a given embedding $\iota : S ^ { k } \rightarrow ( M ^ { 2 n - 1 } , \xi )$ by an isotropic embedding $\iota_0$ (for $k \leq n - 1$) that is isotopic to the initial one, provided only an obvious necessary bundle condition is satisfied: If $\iota_0$ is an isotropic embedding, then its differential $T _ { \iota 0 }$ extends to a complex bundle monomorphism $T S ^ { k } \otimes \mathbf{C} \rightarrow \xi$, where $\xi $ inherits a complex structure from the (conformal) symplectic structure $d \alpha |_\xi$. The relevant $h$-principle says that, conversely, the existence of such a bundle mapping covering <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120200/c12020054.png"/> is sufficient for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120200/c12020055.png"/> to be isotopic to an isotropic embedding $\iota_0$. | |
| + | |||
| + | This allows one to use topological structure theorems, such as Barden's classification of simply-connected $5$-manifolds [[#References|[a1]]], to construct contact structures on a wide class of higher-dimensional manifolds, see [[#References|[a3]]]. | ||
| + | |||
| + | In dimension $3$ ($n = 2$) there is a different notion of contact surgery, due to R. Lutz and J. Martinet [[#References|[a7]]]; it allows surgery along $1$-spheres embedded transversely to a contact structure $\xi $. This was used by Lutz and Martinet to show the existence of a contact structure on any closed, orientable $3$-manifold and in any homotopy class of $2$-plane fields. For applications of other topological structure theorems (such as branched coverings or open book decompositions, cf. also [[Open book decomposition|Open book decomposition]]) to the construction of contact manifolds, see [[#References|[a4]]] and references therein. | ||
Other types of surgery compatible with some geometric structure include surgery on manifolds of positive [[Scalar curvature|scalar curvature]] ([[#References|[a6]]], [[#References|[a9]]]) and surgery on manifolds of positive [[Ricci curvature|Ricci curvature]] ([[#References|[a10]]], [[#References|[a12]]]). | Other types of surgery compatible with some geometric structure include surgery on manifolds of positive [[Scalar curvature|scalar curvature]] ([[#References|[a6]]], [[#References|[a9]]]) and surgery on manifolds of positive [[Ricci curvature|Ricci curvature]] ([[#References|[a10]]], [[#References|[a12]]]). | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> D. Barden, "Simply connected five-manifolds" ''Ann. of Math.'' , '''82''' (1965) pp. 365–385 {{MR|0184241}} {{ZBL|0136.20602}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> Y. Eliashberg, "Topological characterization of Stein manifolds of dimension $> 2$" ''Internat. J. Math.'' , '''1''' (1990) pp. 29–46 {{MR|1044658}} {{ZBL|0699.58002}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> H. Geiges, "Applications of contact surgery" ''Topology'' , '''36''' (1997) pp. 1193–1220 {{MR|1452848}} {{ZBL|0912.57019}} </td></tr><tr><td valign="top">[a4]</td> <td valign="top"> H. Geiges, "Constructions of contact manifolds" ''Math. Proc. Cambridge Philos. Soc.'' , '''121''' (1997) pp. 455–464 {{MR|1434654}} {{ZBL|0882.57007}} </td></tr><tr><td valign="top">[a5]</td> <td valign="top"> R.E. Gompf, "Handlebody construction of Stein surfaces" ''Ann. of Math.'' , '''148''' (1998) pp. 619–693 {{MR|1668563}} {{ZBL|0919.57012}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> M. Gromov, H.B. Lawson Jr., "The classification of simply connected manifolds of positive scalar curvature" ''Ann. of Math.'' , '''111''' (1980) pp. 423–434 {{MR|0577131}} {{ZBL|0463.53025}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> J. Martinet, "Formes de contact sur les variétés de dimension$3$" , ''Proc. Liverpool Singularities Sympos. II'' , ''Lecture Notes Math.'' , '''209''' , Springer (1971) pp. 142–163 {{MR|0350771}} {{ZBL|0215.23003}} </td></tr><tr><td valign="top">[a8]</td> <td valign="top"> J. Milnor, "Morse theory" , Princeton Univ. Press (1963) {{MR|0163331}} {{ZBL|0108.10401}} </td></tr><tr><td valign="top">[a9]</td> <td valign="top"> R. Schoen, S.T. Yau, "On the structure of manifolds with positive scalar curvature" ''Manuscripta Math.'' , '''28''' (1979) pp. 159–183 {{MR|0535700}} {{ZBL|0423.53032}} </td></tr><tr><td valign="top">[a10]</td> <td valign="top"> J.-P. Sha, D.-G. Yang, "Positive Ricci curvature on the connected sum of $S ^ { n } \times S ^ { m }$" ''J. Diff. Geom.'' , '''33''' (1991) pp. 127–137 {{MR|1085137}} {{ZBL|}} </td></tr><tr><td valign="top">[a11]</td> <td valign="top"> A. Weinstein, "Contact surgery and symplectic handlebodies" ''Hokkaido Math. J.'' , '''20''' (1991) pp. 241–251 {{MR|1114405}} {{ZBL|0737.57012}} </td></tr><tr><td valign="top">[a12]</td> <td valign="top"> D. Wraith, "Surgery on Ricci positive manifolds" ''J. Reine Angew. Math.'' , '''501''' (1998) pp. 99–113 {{MR|1637825}} {{ZBL|0915.53018}} </td></tr></table> |
Revision as of 16:56, 1 July 2020
A special type of surgery on a (strict) contact manifold $( M ^ { 2 n - 1 } , \xi )$ (i.e. a smooth manifold admitting a (strict) contact structure $\xi = \operatorname{ker} \alpha$, where $\alpha$ is a $1$-form satisfying $\alpha \wedge ( d \alpha ) ^ { n - 1 } \neq 0$), which results in a new contact manifold.
In topological terms, surgery on 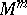 denotes the replacement of an embedded copy of $S ^ { k } \times D ^ { m - k }$, a tubular neighbourhood of an embedded $k$-sphere with trivial normal bundle, by a copy of $D ^ { k + 1 } \times S ^ { m - k - 1 }$, with the obvious identification along the boundary $S ^ { k } \times S ^ { m - k - 1 }$. Alternatively, one can attach a $( k + 1 )$-handle $D ^ { k + 1 } \times D ^ { m - k }$ along $S ^ { k } \times D ^ { m - k }$ to a manifold $W ^ { m + 1 }$ with boundary
denotes the replacement of an embedded copy of $S ^ { k } \times D ^ { m - k }$, a tubular neighbourhood of an embedded $k$-sphere with trivial normal bundle, by a copy of $D ^ { k + 1 } \times S ^ { m - k - 1 }$, with the obvious identification along the boundary $S ^ { k } \times S ^ { m - k - 1 }$. Alternatively, one can attach a $( k + 1 )$-handle $D ^ { k + 1 } \times D ^ { m - k }$ along $S ^ { k } \times D ^ { m - k }$ to a manifold $W ^ { m + 1 }$ with boundary 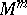 , and the new boundary will be the result of performing surgery on
, and the new boundary will be the result of performing surgery on 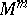 .
.
As shown by Y. Eliashberg [a2] and A. Weinstein [a11], contact surgery is possible along spheres which are isotropic submanifolds (cf. also Isotropic submanifold) of $( M , \xi )$ and have trivial normal bundle. The choice of framing, i.e. trivialization of the normal bundle, for which contact surgery is possible is restricted.
A contact manifold $( M , \xi = \operatorname { ker } \alpha )$ may be regarded as the strictly pseudo-convex boundary of an almost-complex (in fact, symplectic) manifold $W = ( M \times ( 0,1 ] , J )$ such that $\xi $ is given by the $J$-invariant subspace of the tangent bundle $T M$. Contact surgery on $M$ can then be interpreted as the attaching of an almost-complex or symplectic handle to $W$ along $M$, and the framing condition for $n > 2$ is given by requiring the almost-complex structure on $W$ to extend over the handle. For $n = 2$ the situation is more subtle, see [a2], [a5]. Weinstein formulates his construction in terms of symplectic handle-bodies, Eliashberg (whose results are somewhat stronger) in terms of $J$-convex Morse functions on almost-complex manifolds (cf. also Almost-complex structure; Morse function).
A Stein manifold of real dimension $2 n$ has the homotopy type of an $n$-dimensional CW-complex, cf. [a8], p. 39. Eliashberg uses his construction to show that for $n > 2$ this is indeed the only topological restriction on a Stein manifold, that is, if $W$ is a $2 n$-dimensional smooth manifold with an almost-complex structure $J$ and a proper Morse function $\varphi$ with critical points of Morse index at most $n$, then $J$ is homotopic to a genuine complex structure $J ^ { \prime }$ such that $\varphi$ is $J ^ { \prime }$-convex and, in particular, $( W , J ^ { \prime } )$ is Stein.
The usefulness of contact surgery in this and other applications rests on the fact that there is an $h$-principle for isotropic spheres. This allows one to replace a given embedding $\iota : S ^ { k } \rightarrow ( M ^ { 2 n - 1 } , \xi )$ by an isotropic embedding $\iota_0$ (for $k \leq n - 1$) that is isotopic to the initial one, provided only an obvious necessary bundle condition is satisfied: If $\iota_0$ is an isotropic embedding, then its differential $T _ { \iota 0 }$ extends to a complex bundle monomorphism $T S ^ { k } \otimes \mathbf{C} \rightarrow \xi$, where $\xi $ inherits a complex structure from the (conformal) symplectic structure $d \alpha |_\xi$. The relevant $h$-principle says that, conversely, the existence of such a bundle mapping covering  is sufficient for
is sufficient for  to be isotopic to an isotropic embedding $\iota_0$.
to be isotopic to an isotropic embedding $\iota_0$.
This allows one to use topological structure theorems, such as Barden's classification of simply-connected $5$-manifolds [a1], to construct contact structures on a wide class of higher-dimensional manifolds, see [a3].
In dimension $3$ ($n = 2$) there is a different notion of contact surgery, due to R. Lutz and J. Martinet [a7]; it allows surgery along $1$-spheres embedded transversely to a contact structure $\xi $. This was used by Lutz and Martinet to show the existence of a contact structure on any closed, orientable $3$-manifold and in any homotopy class of $2$-plane fields. For applications of other topological structure theorems (such as branched coverings or open book decompositions, cf. also Open book decomposition) to the construction of contact manifolds, see [a4] and references therein.
Other types of surgery compatible with some geometric structure include surgery on manifolds of positive scalar curvature ([a6], [a9]) and surgery on manifolds of positive Ricci curvature ([a10], [a12]).
References
| [a1] | D. Barden, "Simply connected five-manifolds" Ann. of Math. , 82 (1965) pp. 365–385 MR0184241 Zbl 0136.20602 |
| [a2] | Y. Eliashberg, "Topological characterization of Stein manifolds of dimension $> 2$" Internat. J. Math. , 1 (1990) pp. 29–46 MR1044658 Zbl 0699.58002 |
| [a3] | H. Geiges, "Applications of contact surgery" Topology , 36 (1997) pp. 1193–1220 MR1452848 Zbl 0912.57019 |
| [a4] | H. Geiges, "Constructions of contact manifolds" Math. Proc. Cambridge Philos. Soc. , 121 (1997) pp. 455–464 MR1434654 Zbl 0882.57007 |
| [a5] | R.E. Gompf, "Handlebody construction of Stein surfaces" Ann. of Math. , 148 (1998) pp. 619–693 MR1668563 Zbl 0919.57012 |
| [a6] | M. Gromov, H.B. Lawson Jr., "The classification of simply connected manifolds of positive scalar curvature" Ann. of Math. , 111 (1980) pp. 423–434 MR0577131 Zbl 0463.53025 |
| [a7] | J. Martinet, "Formes de contact sur les variétés de dimension$3$" , Proc. Liverpool Singularities Sympos. II , Lecture Notes Math. , 209 , Springer (1971) pp. 142–163 MR0350771 Zbl 0215.23003 |
| [a8] | J. Milnor, "Morse theory" , Princeton Univ. Press (1963) MR0163331 Zbl 0108.10401 |
| [a9] | R. Schoen, S.T. Yau, "On the structure of manifolds with positive scalar curvature" Manuscripta Math. , 28 (1979) pp. 159–183 MR0535700 Zbl 0423.53032 |
| [a10] | J.-P. Sha, D.-G. Yang, "Positive Ricci curvature on the connected sum of $S ^ { n } \times S ^ { m }$" J. Diff. Geom. , 33 (1991) pp. 127–137 MR1085137 |
| [a11] | A. Weinstein, "Contact surgery and symplectic handlebodies" Hokkaido Math. J. , 20 (1991) pp. 241–251 MR1114405 Zbl 0737.57012 |
| [a12] | D. Wraith, "Surgery on Ricci positive manifolds" J. Reine Angew. Math. , 501 (1998) pp. 99–113 MR1637825 Zbl 0915.53018 |
Contact surgery. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contact_surgery&oldid=24403