Difference between revisions of "Tilted algebra"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (AUTOMATIC EDIT (latexlist): Replaced 67 formulas out of 69 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 69 formulas, 67 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
The endomorphism ring of a [[Tilting module|tilting module]] over a finite-dimensional hereditary algebra (cf. also [[Algebra|Algebra]]; [[Endomorphism|Endomorphism]]). | The endomorphism ring of a [[Tilting module|tilting module]] over a finite-dimensional hereditary algebra (cf. also [[Algebra|Algebra]]; [[Endomorphism|Endomorphism]]). | ||
| − | Let | + | Let $H$ be a finite-dimensional hereditary $K$-algebra, $K$ some field, for example the path-algebra of some finite [[Quiver|quiver]] without oriented cycles. A finite-dimensional $H$-module $\square _ { H } T$ is called a tilting module if |
| − | i) | + | i) $\operatorname {p.dim} T \leq 1$, which always is satisfied in this context; |
| − | ii) | + | ii) $\operatorname { Ext } _ { H } ^ { 1 } ( T , T ) = 0$; and |
| − | iii) there exists a short [[Exact sequence|exact sequence]] | + | iii) there exists a short [[Exact sequence|exact sequence]] $0 \rightarrow H \rightarrow T _ { 1 } \rightarrow T _ { 2 } \rightarrow 0$ with $T _ { 1 }$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130100/t13010010.png"/> in $\operatorname{add} T$, the category of finite direct sums of direct summands of $T$. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130100/t13010013.png"/> is projective dimension. The third condition also says that $T$ is maximal with respect to the property $\operatorname { Ext } _ { H } ^ { 1 } ( T , T ) = 0$. Note further, that a tilting module $T$ over a hereditary algebra is uniquely determined by its composition factors. Cf. also [[Tilting module|Tilting module]]. |
| − | The algebra | + | The algebra $B = \operatorname { End } _ { H } ( T )$ is called a tilted algebra of type $H$, and $T$ becomes an $( H , B )$-bimodule (cf. also [[Bimodule|Bimodule]]). |
| − | In | + | In $H$-mod, the [[Category|category]] of finite-dimensional $H$-modules, the module $T$ defines a torsion pair $( \mathcal{G} , \mathcal{F} )$ with torsion class $\mathcal{G}$ consisting of modules, generated by $T$ and torsion-free class $\mathcal{F} = \{ Y : \operatorname { Hom } _ { H } ( T , Y ) = 0 \}$. In $B$-mod it defines the torsion pair $\cal ( X , Y )$ with torsion class $\chi = \{ Y : T \otimes _ { B } Y = 0 \}$ and torsion-free class $\mathcal{Y} = \{ Y : \operatorname { Tor } _ { 1 } ^ { B } ( T , Y ) = 0 \}$. The Brenner–Butler theorem says that the functors $\operatorname{Hom}_H( T , - )$, respectively $T \otimes_{ B} -$, induce equivalences between $\mathcal{G}$ and $\mathcal{Y}$, whereas $\operatorname { Ext } _ { H } ^ { 1 } ( T , - )$, respectively $\operatorname { Tor } _ { 1 } ^ { B } ( T , - )$, induce equivalences between $\mathcal{F}$ and $\mathcal{X}$. In $B$-mod the torsion pair is splitting, that is, any indecomposable $B$-module is either torsion or torsion-free. In this sense, $B$-mod has "less" indecomposable modules, and information on the category $H$-mod can be transferred to $B$-mod. |
| − | For example, | + | For example, $B$ has global dimension at most $2$ and any indecomposable $B$-module has projective dimension or injective dimension at most $1$ (cf. also [[Dimension|Dimension]] for dimension notions). These condition characterize the more general class of quasi-tilted algebras. |
| − | The indecomposable injective | + | The indecomposable injective $H$-modules are in the torsion class $\mathcal{G}$ and their images under the [[Tilting functor|tilting functor]] $\operatorname{Hom}_H( T , - )$ are contained in one connected component of the Auslander–Reiten quiver $\Gamma ( B )$ of $B$-mod (cf. also [[Quiver|Quiver]]; [[Riedtmann classification|Riedtmann classification]]), and they form a complete slice in this component. Moreover, the existence of such a complete slice in a connected component of $\Gamma ( B )$ characterizes tilted algebras. Moreover, the Auslander–Reiten quiver of a tilted algebra always contains pre-projective and pre-injective components. |
| − | If | + | If $H$ is a basic hereditary algebra and $H e$ is a simple projective module, then $T = H ( 1 - e ) \oplus \operatorname { TrD } H e$, where $\operatorname{Tr}D$ denotes the Auslander–Reiten translation (cf. [[Riedtmann classification|Riedtmann classification]]), is a tilting module, sometimes called APR-tilting module. The induced torsion pair $( \mathcal{G} , \mathcal{F} )$ in $H$-mod is splitting and $H e$ is the unique indecomposable module in $\mathcal{F}$. The tilting functor $\operatorname{Hom}_H( T , - )$ corresponds to the reflection functor introduced by I.N. Bernshtein, I.M. Gel'fand and V.A. Ponomarev for their proof of the Gabriel theorem [[#References|[a4]]]. |
| − | If the hereditary algebra | + | If the hereditary algebra $H$ is representation-finite (cf. also [[Algebra of finite representation type|Algebra of finite representation type]]), then any tilted algebra of type $H$ also is representation-finite. If $H$ is tame (cf. also [[Representation of an associative algebra|Representation of an associative algebra]]), then a tilted algebra of type $H$ either is tame and one-parametric, or representation-finite. The latter case is equivalent to the fact that the tilting module contains non-zero pre-projective and pre-injective direct summands simultaneously. If $H$ is wild (cf. also [[Representation of an associative algebra|Representation of an associative algebra]]), then a tilted algebra of type $H$ may be wild, or tame domestic, or representation-finite. |
See also [[Tilting theory|Tilting theory]]. | See also [[Tilting theory|Tilting theory]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> I. Assem, "Tilting theory - an introduction" N. Balcerzyk (ed.) et al. (ed.) , ''Topics in Algebra'' , '''26''' , Banach Center Publ. (1990) pp. 127–180 {{MR|1171230}} {{ZBL|0726.16008}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> M. Auslander, M.I. Platzeck, I. Reiten, "Coxeter functors without diagrams" ''Trans. Amer. Math. Soc.'' , '''250''' (1979) pp. 1–46 {{MR|0530043}} {{ZBL|0421.16016}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> S. Brenner, M. Butler, "Generalizations of the Bernstein–Gelfand–Ponomarev reflection functors" V. Dlab (ed.) P. Gabriel (ed.) , ''Representation Theory II. Proc. ICRA II'' , ''Lecture Notes in Mathematics'' , '''832''' , Springer (1980) pp. 103–169 {{MR|0607151}} {{ZBL|0446.16031}} </td></tr><tr><td valign="top">[a4]</td> <td valign="top"> I.N. Bernstein, I.M. Gelfand, V.A. Ponomarow, "Coxeter functors and Gabriel's theorem" ''Russian Math. Surveys'' , '''28''' (1973) pp. 17–32</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> K. Bongartz, "Tilted algebras" M. Auslander (ed.) E. Lluis (ed.) , ''Representations of Algebras. Proc. ICRA III'' , ''Lecture Notes in Mathematics'' , '''903''' , Springer (1981) pp. 26–38 {{MR|0654701}} {{ZBL|0478.16025}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> D. Happel, "Triangulated categories in the representation theory of finite dimensional algebras" , ''London Math. Soc. Lecture Notes'' , '''119''' , Cambridge Univ. Press (1988) {{MR|0935124}} {{ZBL|0635.16017}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> D. Happel, C.M. Ringel, "Tilted algebras" ''Trans. Amer. Math. Soc.'' , '''274''' (1982) pp. 399–443 {{MR|0675063}} {{MR|0662711}} {{ZBL|0503.16024}} {{ZBL|0489.16025}} </td></tr><tr><td valign="top">[a8]</td> <td valign="top"> D. Happel, I. Reiten, S.O. Smalø, "Tilting in abelian categories and quasitilted algebras" ''Memoirs Amer. Math. Soc.'' , '''575''' (1996) {{MR|1327209}} {{ZBL|0849.16011}} </td></tr><tr><td valign="top">[a9]</td> <td valign="top"> O. Kerner, "Tilting wild algebras" ''J. London Math. Soc.'' , '''39''' : 2 (1989) pp. 29–47 {{MR|0989917}} {{ZBL|0675.16013}} </td></tr><tr><td valign="top">[a10]</td> <td valign="top"> O. Kerner, "Wild tilted algebras revisited" ''Colloq. Math.'' , '''73''' (1997) pp. 67–81 {{MR|1436951}} {{ZBL|0879.16006}} </td></tr><tr><td valign="top">[a11]</td> <td valign="top"> S. Liu, "The connected components of the Auslander–Reiten quiver of a tilted algebra" ''J. Algebra'' , '''161''' (1993) pp. 505–523 {{MR|1247369}} {{ZBL|0818.16014}} </td></tr><tr><td valign="top">[a12]</td> <td valign="top"> C.M. Ringel, "The regular components of the Auslander–Reiten Quiver of a tilted algebra" ''Chinese Ann. Math. Ser. B.'' , '''9''' (1988) pp. 1–18 {{MR|0943675}} {{ZBL|0667.16024}} </td></tr><tr><td valign="top">[a13]</td> <td valign="top"> C.M. Ringel, "Tame algebras and integral quadratic forms" , ''Lecture Notes in Mathematics'' , '''1099''' , Springer (1984) {{MR|0774589}} {{ZBL|0546.16013}} </td></tr><tr><td valign="top">[a14]</td> <td valign="top"> H. Strauss, "On the perpendicular category of a partial tilting module" ''J. Algebra'' , '''144''' (1991) pp. 43–66 {{MR|1136894}} {{ZBL|0746.16009}} </td></tr></table> |
Revision as of 17:02, 1 July 2020
The endomorphism ring of a tilting module over a finite-dimensional hereditary algebra (cf. also Algebra; Endomorphism).
Let $H$ be a finite-dimensional hereditary $K$-algebra, $K$ some field, for example the path-algebra of some finite quiver without oriented cycles. A finite-dimensional $H$-module $\square _ { H } T$ is called a tilting module if
i) $\operatorname {p.dim} T \leq 1$, which always is satisfied in this context;
ii) $\operatorname { Ext } _ { H } ^ { 1 } ( T , T ) = 0$; and
iii) there exists a short exact sequence $0 \rightarrow H \rightarrow T _ { 1 } \rightarrow T _ { 2 } \rightarrow 0$ with $T _ { 1 }$ and 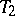 in $\operatorname{add} T$, the category of finite direct sums of direct summands of $T$. Here,
in $\operatorname{add} T$, the category of finite direct sums of direct summands of $T$. Here, 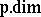 is projective dimension. The third condition also says that $T$ is maximal with respect to the property $\operatorname { Ext } _ { H } ^ { 1 } ( T , T ) = 0$. Note further, that a tilting module $T$ over a hereditary algebra is uniquely determined by its composition factors. Cf. also Tilting module.
is projective dimension. The third condition also says that $T$ is maximal with respect to the property $\operatorname { Ext } _ { H } ^ { 1 } ( T , T ) = 0$. Note further, that a tilting module $T$ over a hereditary algebra is uniquely determined by its composition factors. Cf. also Tilting module.
The algebra $B = \operatorname { End } _ { H } ( T )$ is called a tilted algebra of type $H$, and $T$ becomes an $( H , B )$-bimodule (cf. also Bimodule).
In $H$-mod, the category of finite-dimensional $H$-modules, the module $T$ defines a torsion pair $( \mathcal{G} , \mathcal{F} )$ with torsion class $\mathcal{G}$ consisting of modules, generated by $T$ and torsion-free class $\mathcal{F} = \{ Y : \operatorname { Hom } _ { H } ( T , Y ) = 0 \}$. In $B$-mod it defines the torsion pair $\cal ( X , Y )$ with torsion class $\chi = \{ Y : T \otimes _ { B } Y = 0 \}$ and torsion-free class $\mathcal{Y} = \{ Y : \operatorname { Tor } _ { 1 } ^ { B } ( T , Y ) = 0 \}$. The Brenner–Butler theorem says that the functors $\operatorname{Hom}_H( T , - )$, respectively $T \otimes_{ B} -$, induce equivalences between $\mathcal{G}$ and $\mathcal{Y}$, whereas $\operatorname { Ext } _ { H } ^ { 1 } ( T , - )$, respectively $\operatorname { Tor } _ { 1 } ^ { B } ( T , - )$, induce equivalences between $\mathcal{F}$ and $\mathcal{X}$. In $B$-mod the torsion pair is splitting, that is, any indecomposable $B$-module is either torsion or torsion-free. In this sense, $B$-mod has "less" indecomposable modules, and information on the category $H$-mod can be transferred to $B$-mod.
For example, $B$ has global dimension at most $2$ and any indecomposable $B$-module has projective dimension or injective dimension at most $1$ (cf. also Dimension for dimension notions). These condition characterize the more general class of quasi-tilted algebras.
The indecomposable injective $H$-modules are in the torsion class $\mathcal{G}$ and their images under the tilting functor $\operatorname{Hom}_H( T , - )$ are contained in one connected component of the Auslander–Reiten quiver $\Gamma ( B )$ of $B$-mod (cf. also Quiver; Riedtmann classification), and they form a complete slice in this component. Moreover, the existence of such a complete slice in a connected component of $\Gamma ( B )$ characterizes tilted algebras. Moreover, the Auslander–Reiten quiver of a tilted algebra always contains pre-projective and pre-injective components.
If $H$ is a basic hereditary algebra and $H e$ is a simple projective module, then $T = H ( 1 - e ) \oplus \operatorname { TrD } H e$, where $\operatorname{Tr}D$ denotes the Auslander–Reiten translation (cf. Riedtmann classification), is a tilting module, sometimes called APR-tilting module. The induced torsion pair $( \mathcal{G} , \mathcal{F} )$ in $H$-mod is splitting and $H e$ is the unique indecomposable module in $\mathcal{F}$. The tilting functor $\operatorname{Hom}_H( T , - )$ corresponds to the reflection functor introduced by I.N. Bernshtein, I.M. Gel'fand and V.A. Ponomarev for their proof of the Gabriel theorem [a4].
If the hereditary algebra $H$ is representation-finite (cf. also Algebra of finite representation type), then any tilted algebra of type $H$ also is representation-finite. If $H$ is tame (cf. also Representation of an associative algebra), then a tilted algebra of type $H$ either is tame and one-parametric, or representation-finite. The latter case is equivalent to the fact that the tilting module contains non-zero pre-projective and pre-injective direct summands simultaneously. If $H$ is wild (cf. also Representation of an associative algebra), then a tilted algebra of type $H$ may be wild, or tame domestic, or representation-finite.
See also Tilting theory.
References
| [a1] | I. Assem, "Tilting theory - an introduction" N. Balcerzyk (ed.) et al. (ed.) , Topics in Algebra , 26 , Banach Center Publ. (1990) pp. 127–180 MR1171230 Zbl 0726.16008 |
| [a2] | M. Auslander, M.I. Platzeck, I. Reiten, "Coxeter functors without diagrams" Trans. Amer. Math. Soc. , 250 (1979) pp. 1–46 MR0530043 Zbl 0421.16016 |
| [a3] | S. Brenner, M. Butler, "Generalizations of the Bernstein–Gelfand–Ponomarev reflection functors" V. Dlab (ed.) P. Gabriel (ed.) , Representation Theory II. Proc. ICRA II , Lecture Notes in Mathematics , 832 , Springer (1980) pp. 103–169 MR0607151 Zbl 0446.16031 |
| [a4] | I.N. Bernstein, I.M. Gelfand, V.A. Ponomarow, "Coxeter functors and Gabriel's theorem" Russian Math. Surveys , 28 (1973) pp. 17–32 |
| [a5] | K. Bongartz, "Tilted algebras" M. Auslander (ed.) E. Lluis (ed.) , Representations of Algebras. Proc. ICRA III , Lecture Notes in Mathematics , 903 , Springer (1981) pp. 26–38 MR0654701 Zbl 0478.16025 |
| [a6] | D. Happel, "Triangulated categories in the representation theory of finite dimensional algebras" , London Math. Soc. Lecture Notes , 119 , Cambridge Univ. Press (1988) MR0935124 Zbl 0635.16017 |
| [a7] | D. Happel, C.M. Ringel, "Tilted algebras" Trans. Amer. Math. Soc. , 274 (1982) pp. 399–443 MR0675063 MR0662711 Zbl 0503.16024 Zbl 0489.16025 |
| [a8] | D. Happel, I. Reiten, S.O. Smalø, "Tilting in abelian categories and quasitilted algebras" Memoirs Amer. Math. Soc. , 575 (1996) MR1327209 Zbl 0849.16011 |
| [a9] | O. Kerner, "Tilting wild algebras" J. London Math. Soc. , 39 : 2 (1989) pp. 29–47 MR0989917 Zbl 0675.16013 |
| [a10] | O. Kerner, "Wild tilted algebras revisited" Colloq. Math. , 73 (1997) pp. 67–81 MR1436951 Zbl 0879.16006 |
| [a11] | S. Liu, "The connected components of the Auslander–Reiten quiver of a tilted algebra" J. Algebra , 161 (1993) pp. 505–523 MR1247369 Zbl 0818.16014 |
| [a12] | C.M. Ringel, "The regular components of the Auslander–Reiten Quiver of a tilted algebra" Chinese Ann. Math. Ser. B. , 9 (1988) pp. 1–18 MR0943675 Zbl 0667.16024 |
| [a13] | C.M. Ringel, "Tame algebras and integral quadratic forms" , Lecture Notes in Mathematics , 1099 , Springer (1984) MR0774589 Zbl 0546.16013 |
| [a14] | H. Strauss, "On the perpendicular category of a partial tilting module" J. Algebra , 144 (1991) pp. 43–66 MR1136894 Zbl 0746.16009 |
Tilted algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tilted_algebra&oldid=24132