Difference between revisions of "Complete algebraic variety"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (links) |
||
| Line 1: | Line 1: | ||
| − | A generalization of the concept of a compact complex algebraic variety. A separated variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237101.png" /> is called complete if for any variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237102.png" /> the projection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237103.png" /> is a closed morphism, i.e. it maps closed subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237104.png" /> (in the Zariski topology) into closed subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237105.png" />. There is what is called the valuative completeness criterion: For any discrete valuation ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237106.png" /> with field of fractions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237107.png" /> and any morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237108.png" /> there should be a unique morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237109.png" /> that extends <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371010.png" />. This condition is an analogue of the requirement that any sequence in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371011.png" /> has a limit point. | + | A generalization of the concept of a compact complex algebraic variety. A separated variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237101.png" /> is called complete if for any variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237102.png" /> the projection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237103.png" /> is a closed morphism, i.e. it maps closed subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237104.png" /> (in the [[Zariski topology]]) into closed subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237105.png" />. There is what is called the valuative completeness criterion: For any discrete valuation ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237106.png" /> with [[field of fractions]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237107.png" /> and any morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237108.png" /> there should be a unique morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c0237109.png" /> that extends <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371010.png" />. This condition is an analogue of the requirement that any sequence in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371011.png" /> has a limit point. |
Any projective variety is complete, but not vice versa. For any complete algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371012.png" /> there exists a projective variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371013.png" /> and a projective birational morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371014.png" /> (Chow's lemma). For any algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371015.png" /> there exists an open imbedding into a complete variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371016.png" /> (Nagata's theorem). A generalization of the concept of a complete algebraic variety to the relative case is that of a proper morphism of schemes. | Any projective variety is complete, but not vice versa. For any complete algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371012.png" /> there exists a projective variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371013.png" /> and a projective birational morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371014.png" /> (Chow's lemma). For any algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371015.png" /> there exists an open imbedding into a complete variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023710/c02371016.png" /> (Nagata's theorem). A generalization of the concept of a complete algebraic variety to the relative case is that of a proper morphism of schemes. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR> | ||
| + | </table> | ||
Revision as of 20:50, 28 November 2014
A generalization of the concept of a compact complex algebraic variety. A separated variety  is called complete if for any variety
is called complete if for any variety 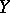 the projection
the projection 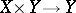 is a closed morphism, i.e. it maps closed subsets of
is a closed morphism, i.e. it maps closed subsets of  (in the Zariski topology) into closed subsets of
(in the Zariski topology) into closed subsets of 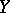 . There is what is called the valuative completeness criterion: For any discrete valuation ring
. There is what is called the valuative completeness criterion: For any discrete valuation ring 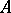 with field of fractions
with field of fractions  and any morphism
and any morphism 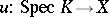 there should be a unique morphism
there should be a unique morphism 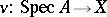 that extends
that extends  . This condition is an analogue of the requirement that any sequence in
. This condition is an analogue of the requirement that any sequence in  has a limit point.
has a limit point.
Any projective variety is complete, but not vice versa. For any complete algebraic variety  there exists a projective variety
there exists a projective variety 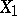 and a projective birational morphism
and a projective birational morphism 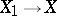 (Chow's lemma). For any algebraic variety
(Chow's lemma). For any algebraic variety 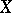 there exists an open imbedding into a complete variety
there exists an open imbedding into a complete variety  (Nagata's theorem). A generalization of the concept of a complete algebraic variety to the relative case is that of a proper morphism of schemes.
(Nagata's theorem). A generalization of the concept of a complete algebraic variety to the relative case is that of a proper morphism of schemes.
References
| [1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
| [2] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
Complete algebraic variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_algebraic_variety&oldid=23792