Complete algebraic variety
A generalization of the concept of a compact complex algebraic variety. A separated variety  is called complete if for any variety
is called complete if for any variety 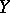 the projection
the projection 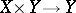 is a closed morphism, i.e. it maps closed subsets of
is a closed morphism, i.e. it maps closed subsets of  (in the Zariski topology) into closed subsets of
(in the Zariski topology) into closed subsets of 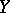 . There is what is called the valuative completeness criterion: For any discrete valuation ring
. There is what is called the valuative completeness criterion: For any discrete valuation ring 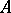 with field of fractions
with field of fractions  and any morphism
and any morphism 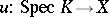 there should be a unique morphism
there should be a unique morphism 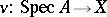 that extends
that extends  . This condition is an analogue of the requirement that any sequence in
. This condition is an analogue of the requirement that any sequence in  has a limit point.
has a limit point.
Any projective variety is complete, but not vice versa. For any complete algebraic variety 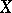 there exists a projective variety
there exists a projective variety 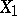 and a projective birational morphism
and a projective birational morphism 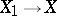 (Chow's lemma). For any algebraic variety
(Chow's lemma). For any algebraic variety 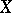 there exists an open imbedding into a complete variety
there exists an open imbedding into a complete variety  (Nagata's theorem). A generalization of the concept of a complete algebraic variety to the relative case is that of a proper morphism of schemes.
(Nagata's theorem). A generalization of the concept of a complete algebraic variety to the relative case is that of a proper morphism of schemes.
References
| [1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [2] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
Complete algebraic variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_algebraic_variety&oldid=11651