Difference between revisions of "Monotone Boolean function"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | m0648201.png | ||
| + | $#A+1 = 61 n = 3 | ||
| + | $#C+1 = 61 : ~/encyclopedia/old_files/data/M064/M.0604820 Monotone Boolean function | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A [[Boolean function|Boolean function]] $ f ( x _ {1} \dots x _ {n} ) $, | |
| + | $ n = 0 , 1 \dots $ | ||
| + | having the following property: If for some sets $ \widetilde \alpha = ( \alpha _ {1} \dots \alpha _ {n} ) $ | ||
| + | and $ \widetilde \beta = ( \beta _ {1} \dots \beta _ {n} ) $, | ||
| + | $ \alpha _ {i} , \beta _ {j} \in \{ 0 , 1 \} $, | ||
| + | the condition $ \alpha _ {i} \leq \beta _ {i} $ | ||
| + | holds for all $ i $( | ||
| + | one then writes $ \widetilde \alpha \prec \widetilde \beta $), | ||
| + | then $ f ( \widetilde \alpha ) \leq f ( \widetilde \beta ) $. | ||
| + | For example, the function $ f ( x _ {1} , x _ {2} ) = x _ {1} \oplus x _ {2} $( | ||
| + | addition modulo 2) is not monotone since $ ( 0 , 1 ) \prec ( 1 , 1 ) $ | ||
| + | but $ 1 = f ( 0 , 1 ) > f ( 1 , 1 ) = 0 $. | ||
| − | + | Examples of monotone Boolean functions are: The constants $ 0 $ | |
| + | and $ 1 $, | ||
| + | the identity function $ f ( x) = x $, | ||
| + | the disjunction $ x _ {1} \lor x _ {2} $, | ||
| + | the conjunction $ x _ {1} \& x _ {2} $, | ||
| + | etc. Examples of non-monotone Boolean functions are: the negation $ \overline{x}\; $, | ||
| + | the implication $ x _ {1} \rightarrow x _ {2} $, | ||
| + | etc. Any function obtained by composition of monotone Boolean functions is itself monotone. In other words, the class of all monotone Boolean functions is closed. Moreover, the class of all monotone Boolean functions is one of the five maximal (pre-complete) classes in the set of all Boolean functions, that is, there is no closed class of Boolean functions containing all monotone Boolean functions and distinct from the class of monotone functions and the class of all Boolean functions. The reduced [[Disjunctive normal form|disjunctive normal form]] of any monotone Boolean function distinct from $ 0 $ | ||
| + | and $ 1 $ | ||
| + | does not contain negations of variables. The set of functions $ \{ 0 , 1 , x _ {1} \lor x _ {2} , x _ {1} \& x _ {2} \} $ | ||
| + | is a complete system (and, moreover, a basis) in the class of all monotone Boolean functions. | ||
| − | + | For the number $ \psi ( n) $ | |
| + | of monotone Boolean functions depending on $ n $ | ||
| + | variables, it is known that | ||
| − | + | $$ | |
| + | \psi ( n) = 2 ^ | ||
| + | {\left ( \begin{array}{c} | ||
| + | n \\ | ||
| + | [ n/2] | ||
| + | \end{array} | ||
| + | \right ) | ||
| + | ( 1 + \epsilon ( n) ) } , | ||
| + | $$ | ||
| − | < | + | where $ 0 < \epsilon ( n) < c ( \mathop{\rm log} n ) / n $ |
| + | and $ c $ | ||
| + | is a constant (see [[#References|[2]]]). | ||
| + | |||
| + | The complexity of realization of the class of monotone Boolean functions by diagrams of functional elements and by switching circuits (cf. [[Diagram of functional elements|Diagram of functional elements]]; [[Contact scheme|Contact scheme]]) has a lower value than the complexity of realization of arbitrary Boolean functions (see [[Synthesis problems|Synthesis problems]]). Certain discrete extremal problems reduce to the problem of evaluating monotone Boolean functions. In this problem it is required, knowing that a function $ f ( x _ {1} \dots x _ {n} ) $ | ||
| + | is a monotone Boolean function, to clarify its value on all sets using fewest possible questions of the form: "What is the value of fa1…an on a certain set a=a1…an?" An algorithm has been suggested, [[#References|[3]]], which for the evaluation of an arbitrary monotone Boolean function requires at most | ||
| + | |||
| + | $$ | ||
| + | \left ( \begin{array}{c} | ||
| + | n \\ | ||
| + | [ n/2] | ||
| + | \end{array} | ||
| + | \right ) + | ||
| + | \left ( \begin{array}{c} | ||
| + | n \\ | ||
| + | [ n/2]+ 1 | ||
| + | \end{array} | ||
| + | \right ) | ||
| + | $$ | ||
questions. On the other hand, there is no evaluation algorithm that would distinguish the function | questions. On the other hand, there is no evaluation algorithm that would distinguish the function | ||
| − | + | $$ | |
| + | f ( x _ {1} \dots x _ {n} ) = \ | ||
| + | \left \{ | ||
among all other monotone Boolean functions in fewer than | among all other monotone Boolean functions in fewer than | ||
| − | + | $$ | |
| + | \left ( \begin{array}{c} | ||
| + | n \\ | ||
| + | [ n/2] | ||
| + | \end{array} | ||
| + | \right ) + | ||
| + | \left ( \begin{array}{c} | ||
| + | n \\ | ||
| + | [ n/2]+ 1 | ||
| + | \end{array} | ||
| + | \right ) | ||
| + | $$ | ||
questions. | questions. | ||
| − | A generalization of the idea of a monotone Boolean function is that of monotone function of | + | A generalization of the idea of a monotone Boolean function is that of monotone function of $ k $- |
| + | valued logic. If an arbitrary partial order $ S $ | ||
| + | is given on the set $ E _ {k} = \{ 0 \dots k - 1 \} $( | ||
| + | written as $ \leq _ {S} $), | ||
| + | then, by definition, for any two sets $ \widetilde \alpha = ( \alpha _ {1} \dots \alpha _ {n} ) $ | ||
| + | and $ \widetilde \beta = ( \beta _ {1} \dots \beta _ {n} ) $, | ||
| + | $ \alpha _ {i} , \beta _ {j} \in E _ {k} $, | ||
| + | $ \widetilde \alpha \prec _ {S} \widetilde \beta $ | ||
| + | means that $ \alpha _ {i} \leq _ {S} \beta _ {i} $ | ||
| + | for all $ i $. | ||
| + | A function of $ k $- | ||
| + | valued logic $ f ( x _ {1} \dots x _ {n} ) $( | ||
| + | that is, defined on and taking values in $ E _ {k} $) | ||
| + | is called monotone relative to $ S $ | ||
| + | if for any sets $ \widetilde \alpha = ( \alpha _ {1} \dots \alpha _ {n} ) $ | ||
| + | and $ \widetilde \beta = ( \beta _ {1} \dots \beta _ {n} ) $, | ||
| + | the condition $ \widetilde \alpha \prec _ {S} \widetilde \beta $ | ||
| + | implies $ f ( \widetilde \alpha ) \leq _ {S} f ( \widetilde \beta ) $. | ||
| + | The class of all functions that are monotone relative to some partial order $ S $ | ||
| + | on $ E _ {k} $ | ||
| + | is always a closed class; it is a pre-complete class in $ k $- | ||
| + | valued logic if and only if there is precisely one maximal element and precisely one minimal element in $ S $[[#References|[4]]]. The number $ \psi _ {S} ( n) $ | ||
| + | of functions of $ k $- | ||
| + | valued logic that depend on $ n $ | ||
| + | variables and that are monotone relative to $ S $ | ||
| + | satisfies, as $ n \rightarrow \infty $, | ||
| − | + | $$ | |
| + | \mathop{\rm log} _ {2} \psi _ {S} ( n) \sim \ | ||
| + | C ( S) | ||
| + | \frac{k ^ {n}}{\sqrt n} | ||
| + | , | ||
| + | $$ | ||
| − | where | + | where $ C ( S) $ |
| + | is a constant that is effectively computable relative to a given partial order $ S $( | ||
| + | see [[#References|[5]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.V. Yablonskii, "Introduction to discrete mathematics" , Moscow (1986) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Kleitman, "On Dedekind's problem: the number of monotone Boolean functions" ''Proc. Amer. Math. Soc.'' , '''21''' (1969) pp. 677–682</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G. Hansel, "Sur le nombre des fonctions booleennes monotones de <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064820/m06482063.png" /> variables" ''C.R. Acad. Paris'' , '''262''' (1966) pp. 1080–1090</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.V. Martynyuk, "Investigation of certain classes of functions in many-valued logics" ''Probl. Kibernet.'' , '''3''' (1960) pp. 49–60 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> V.B. Alekseev, "On the number of monotone <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064820/m06482064.png" />-valued functions" ''Probl. Kibernet.'' , '''28''' (1974) pp. 5–24 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> V.B. Alekseev, "On the number of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064820/m06482065.png" />-valued monotonic functions" ''Soviet Math. Dokl.'' , '''14''' : 1 (1973) pp. 87–91 ''Dokl. Akad. Nauk SSSR'' , '''208''' : 3 (1973) pp. 505–508</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.V. Yablonskii, "Introduction to discrete mathematics" , Moscow (1986) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Kleitman, "On Dedekind's problem: the number of monotone Boolean functions" ''Proc. Amer. Math. Soc.'' , '''21''' (1969) pp. 677–682</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G. Hansel, "Sur le nombre des fonctions booleennes monotones de <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064820/m06482063.png" /> variables" ''C.R. Acad. Paris'' , '''262''' (1966) pp. 1080–1090</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.V. Martynyuk, "Investigation of certain classes of functions in many-valued logics" ''Probl. Kibernet.'' , '''3''' (1960) pp. 49–60 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> V.B. Alekseev, "On the number of monotone <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064820/m06482064.png" />-valued functions" ''Probl. Kibernet.'' , '''28''' (1974) pp. 5–24 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> V.B. Alekseev, "On the number of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064820/m06482065.png" />-valued monotonic functions" ''Soviet Math. Dokl.'' , '''14''' : 1 (1973) pp. 87–91 ''Dokl. Akad. Nauk SSSR'' , '''208''' : 3 (1973) pp. 505–508</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 08:01, 6 June 2020
A Boolean function $ f ( x _ {1} \dots x _ {n} ) $,
$ n = 0 , 1 \dots $
having the following property: If for some sets $ \widetilde \alpha = ( \alpha _ {1} \dots \alpha _ {n} ) $
and $ \widetilde \beta = ( \beta _ {1} \dots \beta _ {n} ) $,
$ \alpha _ {i} , \beta _ {j} \in \{ 0 , 1 \} $,
the condition $ \alpha _ {i} \leq \beta _ {i} $
holds for all $ i $(
one then writes $ \widetilde \alpha \prec \widetilde \beta $),
then $ f ( \widetilde \alpha ) \leq f ( \widetilde \beta ) $.
For example, the function $ f ( x _ {1} , x _ {2} ) = x _ {1} \oplus x _ {2} $(
addition modulo 2) is not monotone since $ ( 0 , 1 ) \prec ( 1 , 1 ) $
but $ 1 = f ( 0 , 1 ) > f ( 1 , 1 ) = 0 $.
Examples of monotone Boolean functions are: The constants $ 0 $ and $ 1 $, the identity function $ f ( x) = x $, the disjunction $ x _ {1} \lor x _ {2} $, the conjunction $ x _ {1} \& x _ {2} $, etc. Examples of non-monotone Boolean functions are: the negation $ \overline{x}\; $, the implication $ x _ {1} \rightarrow x _ {2} $, etc. Any function obtained by composition of monotone Boolean functions is itself monotone. In other words, the class of all monotone Boolean functions is closed. Moreover, the class of all monotone Boolean functions is one of the five maximal (pre-complete) classes in the set of all Boolean functions, that is, there is no closed class of Boolean functions containing all monotone Boolean functions and distinct from the class of monotone functions and the class of all Boolean functions. The reduced disjunctive normal form of any monotone Boolean function distinct from $ 0 $ and $ 1 $ does not contain negations of variables. The set of functions $ \{ 0 , 1 , x _ {1} \lor x _ {2} , x _ {1} \& x _ {2} \} $ is a complete system (and, moreover, a basis) in the class of all monotone Boolean functions.
For the number $ \psi ( n) $ of monotone Boolean functions depending on $ n $ variables, it is known that
$$ \psi ( n) = 2 ^ {\left ( \begin{array}{c} n \\ [ n/2] \end{array} \right ) ( 1 + \epsilon ( n) ) } , $$
where $ 0 < \epsilon ( n) < c ( \mathop{\rm log} n ) / n $ and $ c $ is a constant (see [2]).
The complexity of realization of the class of monotone Boolean functions by diagrams of functional elements and by switching circuits (cf. Diagram of functional elements; Contact scheme) has a lower value than the complexity of realization of arbitrary Boolean functions (see Synthesis problems). Certain discrete extremal problems reduce to the problem of evaluating monotone Boolean functions. In this problem it is required, knowing that a function $ f ( x _ {1} \dots x _ {n} ) $ is a monotone Boolean function, to clarify its value on all sets using fewest possible questions of the form: "What is the value of fa1…an on a certain set a=a1…an?" An algorithm has been suggested, [3], which for the evaluation of an arbitrary monotone Boolean function requires at most
$$ \left ( \begin{array}{c} n \\ [ n/2] \end{array} \right ) + \left ( \begin{array}{c} n \\ [ n/2]+ 1 \end{array} \right ) $$
questions. On the other hand, there is no evaluation algorithm that would distinguish the function
$$ f ( x _ {1} \dots x _ {n} ) = \ \left \{ among all other monotone Boolean functions in fewer than $$ \left ( \begin{array}{c} n \\ [ n/2] \end{array}
\right ) +
\left ( \begin{array}{c} n \\ [ n/2]+ 1 \end{array}
\right )
$$ questions. A generalization of the idea of a monotone Boolean function is that of monotone function of $ k $- valued logic. If an arbitrary partial order $ S $ is given on the set $ E _ {k} = \{ 0 \dots k - 1 \} $( written as $ \leq _ {S} $), then, by definition, for any two sets $ \widetilde \alpha = ( \alpha _ {1} \dots \alpha _ {n} ) $ and $ \widetilde \beta = ( \beta _ {1} \dots \beta _ {n} ) $, $ \alpha _ {i} , \beta _ {j} \in E _ {k} $, $ \widetilde \alpha \prec _ {S} \widetilde \beta $ means that $ \alpha _ {i} \leq _ {S} \beta _ {i} $ for all $ i $. A function of $ k $- valued logic $ f ( x _ {1} \dots x _ {n} ) $( that is, defined on and taking values in $ E _ {k} $) is called monotone relative to $ S $ if for any sets $ \widetilde \alpha = ( \alpha _ {1} \dots \alpha _ {n} ) $ and $ \widetilde \beta = ( \beta _ {1} \dots \beta _ {n} ) $, the condition $ \widetilde \alpha \prec _ {S} \widetilde \beta $ implies $ f ( \widetilde \alpha ) \leq _ {S} f ( \widetilde \beta ) $. The class of all functions that are monotone relative to some partial order $ S $ on $ E _ {k} $ is always a closed class; it is a pre-complete class in $ k $- valued logic if and only if there is precisely one maximal element and precisely one minimal element in $ S $[[#References|[4]]]. The number $ \psi _ {S} ( n) $ of functions of $ k $- valued logic that depend on $ n $ variables and that are monotone relative to $ S $ satisfies, as $ n \rightarrow \infty $, $$
\mathop{\rm log} _ {2} \psi _ {S} ( n) \sim \
C ( S) \frac{k ^ {n}}{\sqrt n}
,
$$
where $ C ( S) $ is a constant that is effectively computable relative to a given partial order $ S $( see [5]).
References
| [1] | S.V. Yablonskii, "Introduction to discrete mathematics" , Moscow (1986) (In Russian) |
| [2] | D. Kleitman, "On Dedekind's problem: the number of monotone Boolean functions" Proc. Amer. Math. Soc. , 21 (1969) pp. 677–682 |
| [3] | G. Hansel, "Sur le nombre des fonctions booleennes monotones de  variables" C.R. Acad. Paris , 262 (1966) pp. 1080–1090 variables" C.R. Acad. Paris , 262 (1966) pp. 1080–1090 |
| [4] | V.V. Martynyuk, "Investigation of certain classes of functions in many-valued logics" Probl. Kibernet. , 3 (1960) pp. 49–60 (In Russian) |
| [5] | V.B. Alekseev, "On the number of monotone 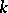 -valued functions" Probl. Kibernet. , 28 (1974) pp. 5–24 (In Russian) -valued functions" Probl. Kibernet. , 28 (1974) pp. 5–24 (In Russian) |
| [6] | V.B. Alekseev, "On the number of 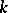 -valued monotonic functions" Soviet Math. Dokl. , 14 : 1 (1973) pp. 87–91 Dokl. Akad. Nauk SSSR , 208 : 3 (1973) pp. 505–508 -valued monotonic functions" Soviet Math. Dokl. , 14 : 1 (1973) pp. 87–91 Dokl. Akad. Nauk SSSR , 208 : 3 (1973) pp. 505–508 |
Comments
In 1985 superpolynomial lower bounds have been proved for the size of monotone circuit realizations of explicit monotone Boolean functions. This solves a problem which had been open since the early days of circuit theory, and which still is open for general Boolean circuits. The first result in this direction was obtained by A.A. Razborov, [a1].
References
| [a1] | A.A. Razborov, "Lower bounds for the monotone complexity of some Boolean functions" Soviet Math. Dokl. , 31 (1985) pp. 354–357 Dokl. Akad. Nauk SSSR , 281 : 4 (1985) pp. 798–801 |
| [a2] | J.E. Savage, "The complexity of computing" , Wiley (1976) |
Monotone Boolean function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monotone_Boolean_function&oldid=18736