Difference between revisions of "Bunyakovskii inequality"
(Importing text file) |
m |
||
| Line 1: | Line 1: | ||
| + | {{TEX|want}} | ||
| + | |||
An equality in mathematical analysis, established by V.Ya. Bunyakovskii [[#References|[1]]] for square-integrable functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017770/b0177701.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017770/b0177702.png" />: | An equality in mathematical analysis, established by V.Ya. Bunyakovskii [[#References|[1]]] for square-integrable functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017770/b0177701.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017770/b0177702.png" />: | ||
Revision as of 07:57, 14 February 2013
An equality in mathematical analysis, established by V.Ya. Bunyakovskii [1] for square-integrable functions 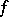 and
and 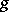 :
:
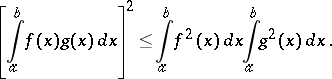 |
This inequality is analogous to Cauchy's algebraic inequality
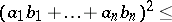 |
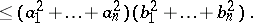 |
The Bunyakovskii inequality is also known as the Schwarz inequality; however, Bunyakovskii published his study as early as 1859, whereas in H.A. Schwarz' work this inequality appeared as late as 1884 (without any reference to the work of Bunyakovskii).
References
| [1] | W. [V.Ya. Bunyakovskii] Bounjakowsky, "Sur quelques inegalités concernant les intégrales aux différences finis" Mem. Acad. Sci. St. Petersbourg (7) , 1 (1859) pp. 9 |
Comments
In Western literature this inequality is often called the Cauchy inequality, or the Cauchy–Schwarz inequality. Its generalization to a function 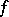 in
in 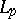 and a function
and a function 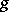 in
in 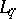 ,
, 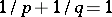 , is called the Hölder inequality.
, is called the Hölder inequality.
Cauchy's algebraic inequality stated above holds for real numbers 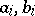 ,
, 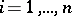 . For complex numbers
. For complex numbers 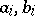 ,
, 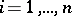 , it reads
, it reads
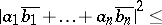 |
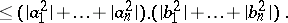 |
It has a generalization analogous to the Hölder inequality.
References
| [a1] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
Bunyakovskii inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bunyakovskii_inequality&oldid=18097