Difference between revisions of "Binomial series"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | b0164301.png | ||
| + | $#A+1 = 31 n = 1 | ||
| + | $#C+1 = 31 : ~/encyclopedia/old_files/data/B016/B.0106430 Binomial series | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A power series of the form | A power series of the form | ||
| − | + | $$ | |
| + | \sum _ { n=0 } ^ \infty | ||
| + | \left ( \begin{array}{c} | ||
| + | \alpha \\ | ||
| + | n | ||
| + | \end{array} | ||
| + | \right ) z ^ {n} = 1 | ||
| + | + \left ( \begin{array}{c} | ||
| + | \alpha \\ | ||
| + | 1 | ||
| + | \end{array} | ||
| + | \right ) z + | ||
| + | \left ( \begin{array}{c} | ||
| + | \alpha \\ | ||
| + | 2 | ||
| + | \end{array} | ||
| + | \right ) z ^ {2} + \dots , | ||
| + | $$ | ||
| − | where | + | where $ n $ |
| + | is an integer and $ \alpha $ | ||
| + | is an arbitrary fixed number (in general, a complex number), $ z = x + iy $ | ||
| + | is a complex variable, and the | ||
| − | + | $$ | |
| + | \left ( \begin{array}{c} | ||
| + | \alpha \\ | ||
| + | n | ||
| + | \end{array} | ||
| + | \right ) | ||
| + | $$ | ||
| − | are the [[Binomial coefficients|binomial coefficients]]. For an integer | + | are the [[Binomial coefficients|binomial coefficients]]. For an integer $ \alpha = m \geq 0 $ |
| + | the binomial series reduces to a finite sum of $ m + 1 $ | ||
| + | terms | ||
| − | + | $$ | |
| + | (1+z) ^ {m} = 1 + mz + | ||
| + | { | ||
| + | \frac{m(m-1)}{2!} | ||
| + | } z ^ {2} + \dots + z ^ {m} , | ||
| + | $$ | ||
| − | which is known as the [[Newton binomial|Newton binomial]]. For other values of | + | which is known as the [[Newton binomial|Newton binomial]]. For other values of $ \alpha $ |
| + | the binomial series converges absolutely for $ | z | <1 $ | ||
| + | and diverges for $ | z | > 1 $. | ||
| + | At points of the unit circle $ | z | = 1 $ | ||
| + | the binomial series behaves as follows: 1) if $ \mathop{\rm Re} \alpha > 0 $, | ||
| + | it converges absolutely at all points; 2) if $ \mathop{\rm Re} \alpha \leq -1 $, | ||
| + | it diverges at all points; and 3) if $ -1 < \mathop{\rm Re} \alpha \leq 0 $, | ||
| + | the binomial series diverges at the point $ z = -1 $ | ||
| + | and converges conditionally at all other points. At all points of convergence, the binomial series represents the principal value of the function $ {(1 + z) } ^ \alpha $ | ||
| + | which is equal to one at $ z = 0 $. | ||
| + | The binomial series is a special case of a [[Hypergeometric series|hypergeometric series]]. | ||
| − | If | + | If $ z = x $ |
| + | and $ \alpha $ | ||
| + | are real numbers, and $ \alpha $ | ||
| + | is not a non-negative integer, the binomial series behaves as follows: 1) if $ \alpha > 0 $, | ||
| + | it converges absolutely on $ -1 \leq x \leq 1 $; | ||
| + | 2) if $ \alpha \leq -1 $, | ||
| + | it converges absolutely in $ -1 < x < 1 $ | ||
| + | and diverges at all other values of $ x $; | ||
| + | and 3) if $ -1 < \alpha \leq 0 $, | ||
| + | the binomial series converges absolutely in $ -1 < x < 1 $, | ||
| + | converges conditionally at $ x = 1 $, | ||
| + | and diverges for $ x = -1 $; | ||
| + | for $ | x | > 1 $ | ||
| + | the binomial series always diverges. | ||
Binomial series were probably first mentioned by I. Newton in 1664–1665. An exhaustive study of binomial series was conducted by N.H. Abel [[#References|[1]]], and was the starting point of the theory of complex power series. | Binomial series were probably first mentioned by I. Newton in 1664–1665. An exhaustive study of binomial series was conducted by N.H. Abel [[#References|[1]]], and was the starting point of the theory of complex power series. | ||
Revision as of 10:59, 29 May 2020
A power series of the form
$$ \sum _ { n=0 } ^ \infty \left ( \begin{array}{c} \alpha \\ n \end{array} \right ) z ^ {n} = 1 + \left ( \begin{array}{c} \alpha \\ 1 \end{array} \right ) z + \left ( \begin{array}{c} \alpha \\ 2 \end{array} \right ) z ^ {2} + \dots , $$
where $ n $ is an integer and $ \alpha $ is an arbitrary fixed number (in general, a complex number), $ z = x + iy $ is a complex variable, and the
$$ \left ( \begin{array}{c} \alpha \\ n \end{array} \right ) $$
are the binomial coefficients. For an integer $ \alpha = m \geq 0 $ the binomial series reduces to a finite sum of $ m + 1 $ terms
$$ (1+z) ^ {m} = 1 + mz + { \frac{m(m-1)}{2!} } z ^ {2} + \dots + z ^ {m} , $$
which is known as the Newton binomial. For other values of $ \alpha $ the binomial series converges absolutely for $ | z | <1 $ and diverges for $ | z | > 1 $. At points of the unit circle $ | z | = 1 $ the binomial series behaves as follows: 1) if $ \mathop{\rm Re} \alpha > 0 $, it converges absolutely at all points; 2) if $ \mathop{\rm Re} \alpha \leq -1 $, it diverges at all points; and 3) if $ -1 < \mathop{\rm Re} \alpha \leq 0 $, the binomial series diverges at the point $ z = -1 $ and converges conditionally at all other points. At all points of convergence, the binomial series represents the principal value of the function $ {(1 + z) } ^ \alpha $ which is equal to one at $ z = 0 $. The binomial series is a special case of a hypergeometric series.
If $ z = x $ and $ \alpha $ are real numbers, and $ \alpha $ is not a non-negative integer, the binomial series behaves as follows: 1) if $ \alpha > 0 $, it converges absolutely on $ -1 \leq x \leq 1 $; 2) if $ \alpha \leq -1 $, it converges absolutely in $ -1 < x < 1 $ and diverges at all other values of $ x $; and 3) if $ -1 < \alpha \leq 0 $, the binomial series converges absolutely in $ -1 < x < 1 $, converges conditionally at $ x = 1 $, and diverges for $ x = -1 $; for $ | x | > 1 $ the binomial series always diverges.
Binomial series were probably first mentioned by I. Newton in 1664–1665. An exhaustive study of binomial series was conducted by N.H. Abel [1], and was the starting point of the theory of complex power series.
References
| [1] | N.H. Abel, "Untersuchungen über die Reihe 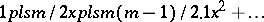 " J. Reine Angew. Math. , 1 (1826) pp. 311–339 " J. Reine Angew. Math. , 1 (1826) pp. 311–339 |
| [2] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) |
| [3] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
Binomial series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Binomial_series&oldid=17445