Difference between revisions of "Morita equivalence"
(Importing text file) |
(LaTeX part) |
||
| Line 1: | Line 1: | ||
| − | + | {{TEX|part}} | |
| − | Alongside with Morita equivalence one considers Morita duality, relating some subcategories of the categories of left | + | An equivalence relation on the class of all [[ring]]s defined as follows: Two rings $R$ and $S$ are called Morita equivalent if the categories of left (right) $R$- and $S$-modules are equivalent. The most important examples of Morita-equivalent rings are: a ring $R$ and the ring of all $n \times n$-matrices over $R$. In order that there is Morita equivalence between two rings $R$ and $S$ it is necessary and sufficient that in the [[category]] of left $R$-modules there is a finitely-generated projective generator $U$ such that its ring of endomorphisms is isomorphic to $S$. The left $R$-module $A$ is put in correspondence with the left $S$-module $\mathrm{Hom}_R(U,A)$. Among the properties preserved by transition to a Morita-equivalent ring are the properties of being: Artinian, Noetherian, primary, simple, classically semi-simple, regular, self-injective, hereditary, and primitive. |
| + | |||
| + | Alongside with Morita equivalence one considers Morita duality, relating some subcategories of the categories of left $R$-modules and right $S$-modules (mostly the subcategories of finitely-generated modules). However, the very existence of such a duality places definite restrictions on the rings $R$ and $S$. In particular, for $R=S$ this implies that $R$ is a [[quasi-Frobenius ring]]. | ||
The general concept of Morita equivalence was developed by K. Morita [[#References|[1]]]. | The general concept of Morita equivalence was developed by K. Morita [[#References|[1]]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> K. Morita, ''Sci. Reports Tokyo Kyoiku Dajkagu A'' , '''6''' (1958) pp. 83–142</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Bass, "Algebraic | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> K. Morita, ''Sci. Reports Tokyo Kyoiku Dajkagu A'' , '''6''' (1958) pp. 83–142</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> H. Bass, "Algebraic $K$-theory" , Benjamin (1968)</TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> C. Faith, "Algebra: rings, modules and categories" , '''1–2''' , Springer (1981–1976)</TD></TR> | ||
| + | <TR><TD valign="top">[4]</TD> <TD valign="top"> P. Cohn, "Morita equivalence and duality" , London (1976)</TD></TR></table> | ||
====Comments==== | ====Comments==== | ||
| − | For generating objects of categories see also [[ | + | For generating objects of categories see also [[Generator of a category]]. |
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493024.png" /> be categories. A duality is a pair of contravariant functors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493025.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493026.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493027.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493028.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493029.png" /> denotes natural equivalence (functorial isomorphism) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493030.png" /> is the identity functor on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493031.png" />. | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493024.png" /> be categories. A duality is a pair of contravariant functors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493025.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493026.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493027.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493028.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493029.png" /> denotes natural equivalence (functorial isomorphism) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493030.png" /> is the identity functor on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493031.png" />. | ||
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493032.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493033.png" /> be rings and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493034.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493035.png" /> be full subcategories of the categories of right <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493036.png" />-modules <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493037.png" /> and left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493038.png" />-modules <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493039.png" />, respectively (cf. [[Module|Module]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493040.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493041.png" /> [[Bimodule|bimodule]]. A duality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493042.png" /> between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493043.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493044.png" /> is called a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493046.png" />-duality or Morita duality if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493047.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493048.png" /> are, respectively, naturally equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493049.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493050.png" />. A theorem of Morita says that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493051.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493052.png" /> are Abelian full subcategories with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493053.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493054.png" />, then any duality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493055.png" /> between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493056.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493057.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493058.png" />-duality with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493059.png" />. | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493032.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493033.png" /> be rings and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493034.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493035.png" /> be full subcategories of the categories of right <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493036.png" />-modules <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493037.png" /> and left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493038.png" />-modules <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493039.png" />, respectively (cf. [[Module|Module]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493040.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493041.png" /> [[Bimodule|bimodule]]. A duality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493042.png" /> between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493043.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493044.png" /> is called a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493046.png" />-duality or Morita duality if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493047.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493048.png" /> are, respectively, naturally equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493049.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493050.png" />. A theorem of Morita says that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493051.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493052.png" /> are Abelian full subcategories with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493053.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493054.png" />, then any duality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493055.png" /> between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493056.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493057.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493058.png" />-duality with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064930/m06493059.png" />. | ||
Revision as of 21:21, 26 November 2014
An equivalence relation on the class of all rings defined as follows: Two rings $R$ and $S$ are called Morita equivalent if the categories of left (right) $R$- and $S$-modules are equivalent. The most important examples of Morita-equivalent rings are: a ring $R$ and the ring of all $n \times n$-matrices over $R$. In order that there is Morita equivalence between two rings $R$ and $S$ it is necessary and sufficient that in the category of left $R$-modules there is a finitely-generated projective generator $U$ such that its ring of endomorphisms is isomorphic to $S$. The left $R$-module $A$ is put in correspondence with the left $S$-module $\mathrm{Hom}_R(U,A)$. Among the properties preserved by transition to a Morita-equivalent ring are the properties of being: Artinian, Noetherian, primary, simple, classically semi-simple, regular, self-injective, hereditary, and primitive.
Alongside with Morita equivalence one considers Morita duality, relating some subcategories of the categories of left $R$-modules and right $S$-modules (mostly the subcategories of finitely-generated modules). However, the very existence of such a duality places definite restrictions on the rings $R$ and $S$. In particular, for $R=S$ this implies that $R$ is a quasi-Frobenius ring.
The general concept of Morita equivalence was developed by K. Morita [1].
References
| [1] | K. Morita, Sci. Reports Tokyo Kyoiku Dajkagu A , 6 (1958) pp. 83–142 |
| [2] | H. Bass, "Algebraic $K$-theory" , Benjamin (1968) |
| [3] | C. Faith, "Algebra: rings, modules and categories" , 1–2 , Springer (1981–1976) |
| [4] | P. Cohn, "Morita equivalence and duality" , London (1976) |
Comments
For generating objects of categories see also Generator of a category.
Let 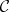 and
and 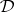 be categories. A duality is a pair of contravariant functors
be categories. A duality is a pair of contravariant functors 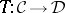 and
and  such that
such that 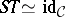 ,
, 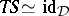 , where
, where 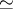 denotes natural equivalence (functorial isomorphism) and
denotes natural equivalence (functorial isomorphism) and  is the identity functor on
is the identity functor on 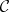 .
.
Let 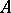 and
and 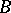 be rings and let
be rings and let 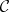 and
and 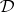 be full subcategories of the categories of right
be full subcategories of the categories of right 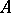 -modules
-modules 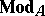 and left
and left 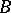 -modules
-modules 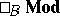 , respectively (cf. Module). Let
, respectively (cf. Module). Let 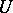 be a
be a 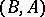 bimodule. A duality
bimodule. A duality 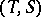 between
between 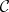 and
and 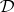 is called a
is called a 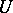 -duality or Morita duality if
-duality or Morita duality if 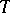 and
and  are, respectively, naturally equivalent to
are, respectively, naturally equivalent to 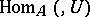 and
and 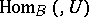 . A theorem of Morita says that if
. A theorem of Morita says that if 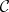 and
and  are Abelian full subcategories with
are Abelian full subcategories with 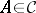 and
and  , then any duality
, then any duality 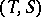 between
between 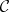 and
and  is a
is a  -duality with
-duality with  .
.
Morita equivalence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Morita_equivalence&oldid=17144