Difference between revisions of "Riemann xi-function"
(Importing text file) |
m (links) |
||
| Line 9: | Line 9: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r1301109.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a2)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r1301109.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a2)</td></tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011010.png" /> denotes the [[Gamma-function|gamma-function]]. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011011.png" /> is a real [[ | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011010.png" /> denotes the [[Gamma-function|gamma-function]]. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011011.png" /> is a real [[entire function]] of order one and of maximal type and satisfies the [[functional equation]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011013.png" /> [[#References|[a6]]], p. 16. By the Hadamard factorization theorem (cf. also [[Hadamard theorem|Hadamard theorem]]), |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011014.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011014.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011015.png" /> ranges over the roots of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011016.png" />. These roots (that is, the zeros of the Riemann <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011017.png" />-function) lie in the strip <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011018.png" />. The celebrated Riemann hypothesis (one of the most important unsolved problems in mathematics as of 2000) asserts that all the roots of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011019.png" /> lie on the critical line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011020.png" /> (cf. [[#References|[a2]]], [[#References|[a1]]], [[#References|[a3]]], [[#References|[a6]]]; cf. also [[ | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011015.png" /> ranges over the roots of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011016.png" />. These roots (that is, the zeros of the Riemann <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011017.png" />-function) lie in the strip <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011018.png" />. The celebrated Riemann hypothesis (one of the most important unsolved problems in mathematics as of 2000) asserts that all the roots of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011019.png" /> lie on the critical line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r130/r130110/r13011020.png" /> (cf. [[#References|[a2]]], [[#References|[a1]]], [[#References|[a3]]], [[#References|[a6]]]; cf. also [[Riemann hypotheses]]). |
The appellation "Riemann x-function" is also used in reference to the function | The appellation "Riemann x-function" is also used in reference to the function | ||
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.M. Edwards, "Riemann's zeta function" , Acad. Press (1974)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Ivić, "The Riemann zeta-function" , Wiley (1985)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.A. Karatsuba, S.M. Voronin, "The Riemann zeta-function" , de Gruyter (1992)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> G. Pólya, "Über die algebraisch-funktionentheoretischen Untersuchungen von J.L.W.V. Jensen" ''Kgl. Danske Vid. Sel. Math.—Fys. Medd.'' , '''7''' (1927) pp. 3–33</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B. Riemann, "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse" ''Monatsber. Preuss. Akad. Wiss.'' (1859) pp. 671–680</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Oxford Univ. Press (1986) ((revised by D.R. Heath–Brown))</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> H.M. Edwards, "Riemann's zeta function" , Acad. Press (1974)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Ivić, "The Riemann zeta-function" , Wiley (1985)</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> A.A. Karatsuba, S.M. Voronin, "The Riemann zeta-function" , de Gruyter (1992)</TD></TR> | ||
| + | <TR><TD valign="top">[a4]</TD> <TD valign="top"> G. Pólya, "Über die algebraisch-funktionentheoretischen Untersuchungen von J.L.W.V. Jensen" ''Kgl. Danske Vid. Sel. Math.—Fys. Medd.'' , '''7''' (1927) pp. 3–33</TD></TR> | ||
| + | <TR><TD valign="top">[a5]</TD> <TD valign="top"> B. Riemann, "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse" ''Monatsber. Preuss. Akad. Wiss.'' (1859) pp. 671–680</TD></TR> | ||
| + | <TR><TD valign="top">[a6]</TD> <TD valign="top"> E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Oxford Univ. Press (1986) ((revised by D.R. Heath–Brown))</TD></TR> | ||
| + | </table> | ||
Revision as of 07:58, 2 January 2015
 -function
-function
In 1859, the newly elected member of the Berlin Academy of Sciences, B.G. Riemann published an epoch-making nine-page paper [a5] (see also [a1], p. 299). In this masterpiece, Riemann's primary goal was to estimate the number of primes less than a given number (cf. also de la Vallée-Poussin theorem). Riemann considers the Euler zeta-function (also called the Riemann zeta-function or Zeta-function)
 | (a1) |
for complex values of  , where the product extends over all prime numbers and the Dirichlet series in (a1) converges for
, where the product extends over all prime numbers and the Dirichlet series in (a1) converges for  (cf. also Zeta-function). His investigation leads him to define a function, called the Riemann
(cf. also Zeta-function). His investigation leads him to define a function, called the Riemann  -function,
-function,
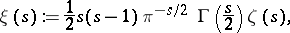 | (a2) |
where 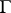 denotes the gamma-function. The function
denotes the gamma-function. The function  is a real entire function of order one and of maximal type and satisfies the functional equation
is a real entire function of order one and of maximal type and satisfies the functional equation 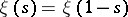 [a6], p. 16. By the Hadamard factorization theorem (cf. also Hadamard theorem),
[a6], p. 16. By the Hadamard factorization theorem (cf. also Hadamard theorem),
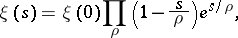 |
where 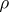 ranges over the roots of the equation
ranges over the roots of the equation 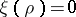 . These roots (that is, the zeros of the Riemann
. These roots (that is, the zeros of the Riemann 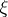 -function) lie in the strip
-function) lie in the strip  . The celebrated Riemann hypothesis (one of the most important unsolved problems in mathematics as of 2000) asserts that all the roots of
. The celebrated Riemann hypothesis (one of the most important unsolved problems in mathematics as of 2000) asserts that all the roots of 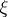 lie on the critical line
lie on the critical line 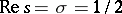 (cf. [a2], [a1], [a3], [a6]; cf. also Riemann hypotheses).
(cf. [a2], [a1], [a3], [a6]; cf. also Riemann hypotheses).
The appellation "Riemann x-function" is also used in reference to the function
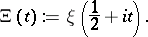 |
(In [a5], Riemann uses the symbol 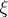 to denote the function which today is denoted by
to denote the function which today is denoted by 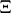 .) In fact, Riemann states his conjecture in terms of the zeros of the Fourier transform [a4], p. 11,
.) In fact, Riemann states his conjecture in terms of the zeros of the Fourier transform [a4], p. 11,
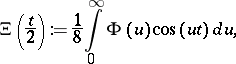 |
where
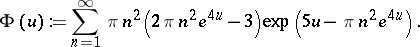 |
The Riemann hypothesis is equivalent to the statement that all the zeros of 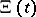 are real (cf. [a6], p. 255). Indeed, Riemann writes "[…] es ist sehr wahrscheinlich, dass alle Wurzeln reell sind." (That is, it is very likely that all the roots of
are real (cf. [a6], p. 255). Indeed, Riemann writes "[…] es ist sehr wahrscheinlich, dass alle Wurzeln reell sind." (That is, it is very likely that all the roots of 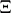 are real.)
are real.)
References
| [a1] | H.M. Edwards, "Riemann's zeta function" , Acad. Press (1974) |
| [a2] | A. Ivić, "The Riemann zeta-function" , Wiley (1985) |
| [a3] | A.A. Karatsuba, S.M. Voronin, "The Riemann zeta-function" , de Gruyter (1992) |
| [a4] | G. Pólya, "Über die algebraisch-funktionentheoretischen Untersuchungen von J.L.W.V. Jensen" Kgl. Danske Vid. Sel. Math.—Fys. Medd. , 7 (1927) pp. 3–33 |
| [a5] | B. Riemann, "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse" Monatsber. Preuss. Akad. Wiss. (1859) pp. 671–680 |
| [a6] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Oxford Univ. Press (1986) ((revised by D.R. Heath–Brown)) |
Riemann xi-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_xi-function&oldid=16941