|
|
| Line 1: |
Line 1: |
| − | The direct scattering problem on the half-axis consists of finding the solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i1300601.png" /> to the problem
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i1300602.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table>
| + | Out of 194 formulas, 193 were replaced by TEX code.--> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i1300603.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a2)</td></tr></table>
| + | {{TEX|semi-auto}}{{TEX|partial}} |
| | + | The direct scattering problem on the half-axis consists of finding the solution $u ( x , k )$ to the problem |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i1300604.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a3)</td></tr></table>
| + | \begin{equation} \tag{a1} u ^ { \prime \prime } + k ^ { 2 } u - q ( x ) u = 0 , x > 0, \end{equation} |
| | | | |
| − | Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i1300605.png" /> is to be determined. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i1300606.png" /> is called the phase shift. The coefficient <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i1300607.png" /> is called the scattering potential. It is assumed to be a real-valued function in the class
| + | \begin{equation} \tag{a2} u ( 0 , k ) = 0 \end{equation} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i1300608.png" /></td> </tr></table>
| + | \begin{equation} \tag{a3} u ( x , k ) = e ^ { i \delta } \operatorname { sin } ( k x + \delta ) + o ( 1 ) , \quad \text { as } x \rightarrow \infty. \end{equation} |
| | | | |
| − | where the bar stands for complex conjugation. The solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i1300609.png" /> to (a1) which satisfies the relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006010.png" />, as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006011.png" />, is called the Jost solution. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006012.png" /> is called the Jost function. One has
| + | Here, $\delta = \delta ( k )$ is to be determined. The function $\delta = \delta ( k )$ is called the phase shift. The coefficient $q ( x )$ is called the scattering potential. It is assumed to be a real-valued function in the class |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006013.png" /></td> </tr></table>
| + | \begin{equation*} L _ { 1,1 } : = \left\{ q : \int _ { 0 } ^ { \infty } x | q ( x ) | d x < \infty , q = \overline { q } \right\}, \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006014.png" /></td> </tr></table>
| + | where the bar stands for complex conjugation. The solution $f ( x , k )$ to (a1) which satisfies the relation $f ( x , k ) = e ^ { i k x } + o ( 1 )$, as $x \rightarrow + \infty$, is called the Jost solution. The function $f ( 0 , k ) : = f ( k )$ is called the Jost function. One has |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006015.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006016.png" /> exists and is unique, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006017.png" /> is analytic in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006018.png" /> and has at most finitely many zeros in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006019.png" />, all of which are simple and of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006020.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006021.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006022.png" />. The numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006023.png" /> are the eigenvalues of the [[Self-adjoint operator|self-adjoint operator]]
| + | \begin{equation*} f ( k ) = | f ( k ) | e ^ { - i \delta ( k ) }, \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006024.png" /></td> </tr></table>
| + | \begin{equation*} \delta ( - k ) = - \delta ( k ) , k \in \mathbf{R} , \quad \delta ( \infty ) = 0. \end{equation*} |
| | | | |
| − | which is determined by the Dirichlet boundary condition at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006025.png" /> in the Hilbert space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006026.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006027.png" /> (cf. also [[Dirichlet boundary conditions|Dirichlet boundary conditions]]). In physics, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006028.png" /> are called the bound states. The positive numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006029.png" /> are called the norming constants. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006030.png" /> is called the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006032.png" />-matrix (cf. [[Scattering matrix|Scattering matrix]]). The triple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006033.png" /> is called the scattering data.
| + | If $q \in L _ { 1 , 1} $, then $f ( x , k )$ exists and is unique, $f ( k )$ is analytic in $\mathbf{C} _ { + } : = \{ k : \operatorname { Im } k > 0 \}$ and has at most finitely many zeros in $\mathbf{C} _ { + }$, all of which are simple and of the form $i k_j$, $k_ j > 0$, $1 \leq j \leq J$. The numbers $- k _ { j } ^ { 2 }$ are the eigenvalues of the [[Self-adjoint operator|self-adjoint operator]] |
| | | | |
| − | The inverse scattering problem consists of finding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006034.png" /> given <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006035.png" />.
| + | \begin{equation*} l : = - \frac { d ^ { 2 } } { d x ^ { 2 } } + q ( x ), \end{equation*} |
| | | | |
| − | The point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006036.png" /> can also be a zero of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006037.png" />. It is called a resonance at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006038.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006039.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006040.png" />. The basic results of inverse scattering theory are (see [[#References|[a5]]], [[#References|[a6]]]):
| + | which is determined by the Dirichlet boundary condition at $x = 0$ in the Hilbert space $L ^ { 2 } ( \mathbf{R} _ { + } )$, $\mathbf{R} _ { + } : = [ 0 , \infty )$ (cf. also [[Dirichlet boundary conditions|Dirichlet boundary conditions]]). In physics, $- k ^ { 2}j $ are called the bound states. The positive numbers $s _ { j } : = \| f ( x , i k _ { j } ) \| ^ { - 2 _{L ^ { 2} ( \mathbf{R} _ { + } )}}$ are called the norming constants. The function $S ( k ) = f ( - k ) / f ( k ) = e ^ { 2 i \delta ( k ) }$ is called the $S$-matrix (cf. [[Scattering matrix|Scattering matrix]]). The triple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006033.png"/> is called the scattering data. |
| | | | |
| − | 1) The uniqueness theorem: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006041.png" />; that is, the scattering data determine <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006042.png" /> uniquely.
| + | The inverse scattering problem consists of finding $q ( x )$ given $\mathcal{S}$. |
| | | | |
| − | 2) The reconstruction theorem: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006043.png" />, corresponding to a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006044.png" />, is given, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006045.png" /> can be reconstructed by the Marchenko method, as follows:''''''<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">1</td> <td colname="2" style="background-color:white;" colspan="1">Calculate
| + | The point $k = 0$ can also be a zero of $f ( k )$. It is called a resonance at $k = 0$. If $f ( 0 ) = 0$, then $f ^ { \prime } ( 0 ) \neq 0$. The basic results of inverse scattering theory are (see [[#References|[a5]]], [[#References|[a6]]]): |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006046.png" /></td> </tr></table>
| + | 1) The uniqueness theorem: $\mathcal{S} \Rightarrow q$; that is, the scattering data determine $q \in L _ { 1 , 1} $ uniquely. |
| | | | |
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">2</td> <td colname="2" style="background-color:white;" colspan="1">Solve the following equation for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006047.png" />: | + | 2) The reconstruction theorem: If $\mathcal{S}$, corresponding to a $q \in L _ { 1 , 1} $, is given, then $q ( x )$ can be reconstructed by the Marchenko method, as follows:''''''<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellpadding="4" cellspacing="1" style="background-color:black;"> <tr> <td colname="1" colspan="1" style="background-color:white;">1</td> <td colname="2" colspan="1" style="background-color:white;">Calculate |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006048.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a4)</td></tr></table>
| + | \begin{equation*} F ( x ) : = \sum _ { j = 1 } ^ { J } s _ { j } e ^ { - k _ { j } x } + \frac { 1 } { 2 \pi } \int _ { - \infty } ^ { \infty } [ 1 - S ( k ) ] e ^ { i k x } d k. \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006049.png" /></td> </tr></table> | + | </td> </tr> <tr> <td colname="1" colspan="1" style="background-color:white;">2</td> <td colname="2" colspan="1" style="background-color:white;">Solve the following equation for $A ( x , y )$: |
| | | | |
| − | This equation is uniquely solvable and is called the Marchenko equatio.</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">3</td> <td colname="2" style="background-color:white;" colspan="1">Calculate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006050.png" />.</td> </tr> </tbody> </table> | + | \begin{equation} \tag{a4} A ( x , y ) + F ( x , y ) + \int _ { x } ^ { \infty } A ( x , s ) F ( s + y ) d s = 0, \end{equation} |
| | + | |
| | + | \begin{equation*} y \geq x \geq 0. \end{equation*} |
| | + | |
| | + | This equation is uniquely solvable and is called the Marchenko equatio.</td> </tr> <tr> <td colname="1" colspan="1" style="background-color:white;">3</td> <td colname="2" colspan="1" style="background-color:white;">Calculate $q ( x ) = - 2 d A ( x , x ) / d x$.</td> </tr> </table> |
| | | | |
| | </td></tr> </table> | | </td></tr> </table> |
| | | | |
| − | 3) The characterization theorem: For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006051.png" /> to be the scattering data corresponding to a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006052.png" /> it is necessary and sufficient that the following conditions hold: | + | 3) The characterization theorem: For $\mathcal{S}$ to be the scattering data corresponding to a $q \in L _ { 1 , 1} $ it is necessary and sufficient that the following conditions hold: |
| | | | |
| − | i) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006053.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006054.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006055.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006056.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006057.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006058.png" />; | + | i) $\overline { S ( k ) } = S ( - k ) = S ^ { - 1 } ( k )$, $k \in {\bf R}_+$; $S ( \infty ) = 1$, $k_ j > 0$, $s _ { j } > 0$, $1 \leq j \leq J$; |
| | | | |
| − | ii) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006060.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006061.png" />; | + | ii) $\operatorname {ind} S ( k ) = - \kappa$, $\kappa = 2 J$ or $\kappa = 2 J + 1$; |
| | | | |
| − | iii) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006062.png" /> | + | iii) $\| F ( x ) \| _ { L^{\infty} ( \mathbf{R} _ { + } ) } + \| F ( x ) \| _ { L ^ { 1 } ( \mathbf{R} _ { + } ) } +$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006063.png" /></td> </tr></table>
| + | \begin{equation*} + \| x F ^ { \prime } ( x ) \| _ { L ^ { 1 } ( \mathbf{R} _ { + } ) } < \infty. \end{equation*} |
| | | | |
| − | Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006064.png" />. | + | Here, $\operatorname{ ind } S ( k ) : = ( 1 / 2 \pi ) \int _ { - \infty } ^ { \infty } d \operatorname { ln } S ( k )$. |
| | | | |
| − | Note that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006065.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006066.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006067.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006068.png" />. The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006069.png" /> is a [[Homeomorphism|homeomorphism]] between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006070.png" /> and the space of the scattering data equipped with the norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006071.png" /> (see [[#References|[a4]]], [[#References|[a5]]] [[#References|[a6]]]). | + | Note that $\kappa = 2 J$ if $f ( 0 ) \neq 0$, and $\kappa = 2 J + 1$ if $f ( 0 ) = 0$. The mapping $T : q \rightarrow \mathcal{S}$ is a [[Homeomorphism|homeomorphism]] between $L _ { 1 , 1}$ and the space of the scattering data equipped with the norm $\| \mathcal{S} \| : = \int _ { 0 } ^ { \infty } ( 1 + x ) | F ^ { \prime } ( x ) | d x$ (see [[#References|[a4]]], [[#References|[a5]]] [[#References|[a6]]]). |
| | | | |
| | One can prove (see [[#References|[a6]]], [[#References|[a13]]]) the diagram | | One can prove (see [[#References|[a6]]], [[#References|[a13]]]) the diagram |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006072.png" /></td> </tr></table>
| + | \begin{equation*} \delta \Leftrightarrow F \Leftrightarrow A \Leftrightarrow q, \end{equation*} |
| | | | |
| − | each step of which is invertible. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006073.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006074.png" /> are defined above. This result guarantees, in particular, that the potential recovered by the Marchenko method generates the original scattering data (provided that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006075.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006076.png" /> satisfies the characterization conditions). | + | each step of which is invertible. Here, $F = F ( x )$ and $A = A ( x , y )$ are defined above. This result guarantees, in particular, that the potential recovered by the Marchenko method generates the original scattering data (provided that $q \in L _ { 1 , 1} $ or $\mathcal{S}$ satisfies the characterization conditions). |
| | | | |
| − | Other methods for solving the inverse scattering problem on the half-axis are based on the solution of the inverse problem of recovery of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006077.png" /> from the [[Spectral function|spectral function]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006078.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006079.png" />) and the Krein method ([[#References|[a1]]], [[#References|[a3]]], [[#References|[a5]]] [[#References|[a6]]], [[#References|[a15]]]). | + | Other methods for solving the inverse scattering problem on the half-axis are based on the solution of the inverse problem of recovery of $q ( x )$ from the [[Spectral function|spectral function]] $\rho : = \rho ( \lambda )$ ($\mathcal{S} \Rightarrow \rho \Rightarrow q$) and the Krein method ([[#References|[a1]]], [[#References|[a3]]], [[#References|[a5]]] [[#References|[a6]]], [[#References|[a15]]]). |
| | | | |
| − | The scattering data are in one-to-one correspondence with the spectral function [[#References|[a6]]] [[#References|[a7]]], [[#References|[a13]]]. Recovery of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006080.png" /> given the spectral function is discussed in [[#References|[a1]]], [[#References|[a3]]], [[#References|[a5]]], [[#References|[a6]]]. | + | The scattering data are in one-to-one correspondence with the spectral function [[#References|[a6]]] [[#References|[a7]]], [[#References|[a13]]]. Recovery of $q ( x )$ given the spectral function is discussed in [[#References|[a1]]], [[#References|[a3]]], [[#References|[a5]]], [[#References|[a6]]]. |
| | | | |
| − | The original work of M.G. Krein [[#References|[a2]]] and its review in [[#References|[a1]]] do not contain proofs. A detailed presentation of Krein's theory with complete proofs is given in [[#References|[a15]]] for the first time. Also, a proof of consistency of Krein's method is given in [[#References|[a15]]]. In [[#References|[a2]]] (and in [[#References|[a1]]]) there is no discussion of the consistency of Krein's method. By the consistency of an inversion method one means a proof of the implication <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006081.png" /> (the reconstructed potential generates the data from which it was reconstructed). | + | The original work of M.G. Krein [[#References|[a2]]] and its review in [[#References|[a1]]] do not contain proofs. A detailed presentation of Krein's theory with complete proofs is given in [[#References|[a15]]] for the first time. Also, a proof of consistency of Krein's method is given in [[#References|[a15]]]. In [[#References|[a2]]] (and in [[#References|[a1]]]) there is no discussion of the consistency of Krein's method. By the consistency of an inversion method one means a proof of the implication $q \Rightarrow \mathcal{S}$ (the reconstructed potential generates the data from which it was reconstructed). |
| | | | |
| − | Below, Krein's method is described under the simplifying assumption <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006082.png" /> (no bound states and no resonance at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006083.png" />). The general case is treated in [[#References|[a15]]].''''''<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">1</td> <td colname="2" style="background-color:white;" colspan="1">Given <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006084.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006085.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006086.png" />, one finds <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006087.png" />, then calculates | + | Below, Krein's method is described under the simplifying assumption $\kappa = 0$ (no bound states and no resonance at $k = 0$). The general case is treated in [[#References|[a15]]].''''''<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellpadding="4" cellspacing="1" style="background-color:black;"> <tr> <td colname="1" colspan="1" style="background-color:white;">1</td> <td colname="2" colspan="1" style="background-color:white;">Given $S ( k ) = e ^ { 2 i \delta ( k ) }$, $\operatorname{ind} S ( k ) = 0$, $\delta ( \infty ) = 0$, one finds $\delta ( k )$, then calculates |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006088.png" /></td> </tr></table>
| + | \begin{equation*} g ( t ) : = - \frac { 2 } { \pi } \int _ { 0 } ^ { \infty } \delta ( k ) \operatorname { sin } ( k t ) d k, \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006089.png" /></td> </tr></table>
| + | \begin{equation*} f ( k ) = \operatorname { exp } ( \int _ { 0 } ^ { \infty } g ( t ) e ^ { i k t } d t ), \end{equation*} |
| | | | |
| | and | | and |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006090.png" /></td> </tr></table>
| + | \begin{equation*} H ( t ) : = - \frac { 1 } { 2 \pi } \int _ { - \infty } ^ { \infty } \left( | f ( k ) | ^ { - 2 } - 1 \right) e ^ { - i k t } d k. \end{equation*} |
| | | | |
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">2</td> <td colname="2" style="background-color:white;" colspan="1">Given <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006091.png" />, one solves the equation | + | </td> </tr> <tr> <td colname="1" colspan="1" style="background-color:white;">2</td> <td colname="2" colspan="1" style="background-color:white;">Given $H ( t )$, one solves the equation |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006092.png" /></td> </tr></table>
| + | \begin{equation*} ( I + H _ { x } ) \Gamma _ { x } : = \Gamma _ { x } ( t , s ) + \int _ { 0 } ^ { x } H ( t - u ) \Gamma _ { x } ( u , s ) d u = H ( t - s ) ,\, 0 \leq t , s \leq x, \end{equation*} |
| | | | |
| − | for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006093.png" /> and finds <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006094.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006095.png" />.</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006096.png" />, and calculates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006097.png" />. Alternatively, | + | for $\Gamma _ { x } ( t , s )$ and finds $\Gamma _ { 2 x } ( 2 x , 0 )$, $0 \leq x < \infty$.</td> </tr> <tr> <td colname="1" colspan="1" style="background-color:white;">$A ( x ) = 2 \Gamma _ { 2 x } ( 2 x , 0 )$, and calculates $q ( x ) = A ^ { 2 } ( x ) + A ^ { \prime } ( x )$. Alternatively, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006098.png" /></td> </tr></table>
| + | \begin{equation*} q ( x ) = 2 \frac { d } { d x } [ \Gamma _ { 2 x } ( 2 x , 0 ) - \Gamma _ { 2 x } ( 0,0 ) ]. \end{equation*} |
| | | | |
| − | </td> </tr> </tbody> </table> | + | </td> </tr> </table> |
| | | | |
| | </td></tr> </table> | | </td></tr> </table> |
| | | | |
| − | In Step 1, one can find <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i13006099.png" /> by a different method: Solve the Riemann problem | + | In Step 1, one can find $f ( k )$ by a different method: Solve the Riemann problem |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060100.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a5)</td></tr></table>
| + | \begin{equation} \tag{a5} \varphi_{+} ( k ) = S ( - k ) \varphi _ { - } ( k ), \end{equation} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060101.png" /></td> </tr></table>
| + | \begin{equation*} k \in \mathbf{R} , \varphi _ { \pm } ( \infty ) = 1. \end{equation*} |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060102.png" />, this problem has the unique solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060103.png" />. One has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060104.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060105.png" />. | + | If $\operatorname{ind} S ( k ) = 0$, this problem has the unique solution $\{ \varphi_+ ( k ) , \varphi_- ( k ) \}$. One has $\varphi _ { + } ( k ) = f ( k )$, $\varphi_{-} ( k ) = f ( - k )$. |
| | | | |
| − | Note that the data <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060106.png" /> allow one to find a unique <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060107.png" /> by solving the Riemann problem (a5) with the additional conditions: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060108.png" /> has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060109.png" /> simple zeros at the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060110.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060111.png" /> and, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060112.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060113.png" /> has, in addition, a simple zero at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060114.png" />. Thus, the data <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060115.png" /> is equivalent to the data <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060116.png" />. | + | Note that the data $\mathcal{S}$ allow one to find a unique $f ( k )$ by solving the Riemann problem (a5) with the additional conditions: $\varphi_{+} ( k )$ has $J$ simple zeros at the points $i k_j$ if $\kappa = - 2 J$ and, if $\kappa = - 2 J - 1$, $\varphi_{+} ( k )$ has, in addition, a simple zero at $k = 0$. Thus, the data $\mathcal{S}$ is equivalent to the data $\{ f ( k ) , s _j 1 \leq j \leq J \}$. |
| | | | |
| − | An inverse problem of recovery of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060117.png" /> from incomplete scattering data but with an a priori assumption that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060118.png" /> has compact support is investigated in [[#References|[a8]]] [[#References|[a9]]]. It is proved that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060119.png" /> is compactly supported and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060120.png" /> is known for a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060121.png" /> which has a finite limit point inside <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060122.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060123.png" /> is determined uniquely. An algorithm for finding a compactly supported <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060124.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060125.png" /> (that is, from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060126.png" />) known for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060127.png" /> is given in [[#References|[a8]]]. A uniqueness theorem for the problem of finding a compactly supported <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060128.png" /> from the knowledge of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060129.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060130.png" />, is proved in [[#References|[a13]]]. | + | An inverse problem of recovery of $q ( x )$ from incomplete scattering data but with an a priori assumption that $q ( x )$ has compact support is investigated in [[#References|[a8]]] [[#References|[a9]]]. It is proved that if $q \in L _ { 1 , 1} $ is compactly supported and if $\delta ( k )$ is known for a sequence $k = k _ { n } > 0$ which has a finite limit point inside $( 0 , \infty )$, then $q ( x )$ is determined uniquely. An algorithm for finding a compactly supported $q ( x )$ from $\delta ( k )$ (that is, from $\mathcal{S} ( k )$) known for all $k > 0$ is given in [[#References|[a8]]]. A uniqueness theorem for the problem of finding a compactly supported $q ( x )$ from the knowledge of $f ^ { \prime } ( 0 , k )$, $\forall k > 0$, is proved in [[#References|[a13]]]. |
| | | | |
| − | In [[#References|[a7]]], [[#References|[a12]]] an algorithm for recovery of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060131.png" /> from the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060132.png" />-function is given, where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060134.png" />-function is identical with the Weyl function. | + | In [[#References|[a7]]], [[#References|[a12]]] an algorithm for recovery of $q ( x )$ from the $I$-function is given, where the $I$-function is identical with the Weyl function. |
| | | | |
| − | For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060135.png" /> to belong to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060136.png" /> it is necessary and sufficient [[#References|[a6]]] that | + | For $q \in L _ { 1 , 1} $ to belong to $L ^ { 2 } ( \mathbf{R} _ { + } )$ it is necessary and sufficient [[#References|[a6]]] that |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060137.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a6)</td></tr></table>
| + | \begin{equation} \tag{a6} k \left[ 1 - S ( k ) + \frac { Q } { i k } \right] \in L ^ { 2 } ( \mathbf{R} ), \end{equation} |
| | | | |
| | where | | where |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060138.png" /></td> </tr></table>
| + | \begin{equation*} Q : = \int _ { 0 } ^ { \infty } q ( t ) d t = - 2 i \operatorname { lim } _ { k \rightarrow \infty } \{ k [ f ( k ) - 1 ] \}. \end{equation*} |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060139.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060140.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060141.png" />, is compactly supported, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060142.png" /> is an [[Entire function|entire function]] of exponential type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060143.png" />. Its zeros in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060144.png" /> are called resonances. | + | If $q ( x ) \in L _ { 1,1 } \cap L ^ { 2 } ( \mathbf{R} _ { + } )$, $q = 0$ for $x \geq a$, is compactly supported, then $f ( k )$ is an [[Entire function|entire function]] of exponential type $\leq 2 a$. Its zeros in $\mathbf{C} _ { - } : = \{ k : \operatorname { Im } k < 0 \}$ are called resonances. |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060145.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060146.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060147.png" />, then there are infinitely many resonances [[#References|[a6]]]. | + | If $q ( x ) \not\equiv 0$, $\int _ { 0 } ^ { \infty } x ^ { n } | q ( x ) | d x = o ( n ^ { b n } )$, $0 \leq b < 1$, then there are infinitely many resonances [[#References|[a6]]]. |
| | | | |
| − | There exists a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060148.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060149.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060150.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060151.png" /> is arbitrary small, which generates infinitely many purely imaginary resonances [[#References|[a6]]]. | + | There exists a $q ( x ) \in C _ { 0 } ^ { \infty } ( \mathbf{R} + )$, $q ( x ) = 0$ for $x \geq \epsilon$, where $\epsilon > 0$ is arbitrary small, which generates infinitely many purely imaginary resonances [[#References|[a6]]]. |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060152.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060153.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060154.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060155.png" /> does not change sign in an interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060156.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060157.png" /> is arbitrarily small, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060158.png" /> generates only finitely many purely imaginary resonances (a6). | + | If $q ( x ) \in L _ { 1,1 }$, $q ( x ) = 0$ for $x \geq a$ and $q ( x )$ does not change sign in an interval $( a - \delta , a )$, where $\delta > 0$ is arbitrarily small, then $q ( x )$ generates only finitely many purely imaginary resonances (a6). |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060159.png" />, then the following estimate (see [[#References|[a5]]]) is useful: | + | If $q \in L _ { 1 , 1} $, then the following estimate (see [[#References|[a5]]]) is useful: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060160.png" /></td> </tr></table>
| + | \begin{equation*} \left| F ^ { \prime } ( 2 x ) - \frac { q ( x ) } { 4 } + \frac { 1 } { 4 } \left( \int _ { x } ^ { \infty } q ( t ) d t \right)^2 \right| \leq c \sigma ^ { 2 } ( x ), \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060161.png" /></td> </tr></table>
| + | \begin{equation*} \sigma ( x ) : = \int _ { x } ^ { \infty } | q ( t ) | d t. \end{equation*} |
| | | | |
| − | The Jost solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060162.png" /> can be written as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060163.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060164.png" /> is the kernel of the transformation operator. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060165.png" />, then | + | The Jost solution $f ( x , k )$ can be written as $f ( x , k ) = e ^ { i k x } + \int _ { x } ^ { \infty } A ( x , y ) e ^ { i k y } d y$, where $A ( x , y )$ is the kernel of the transformation operator. If $q \in L _ { 1 , 1} $, then |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060166.png" /></td> </tr></table>
| + | \begin{equation*} | F ( 2 x ) + A ( x , x ) | \leq c \sigma ( x ), \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060167.png" /></td> </tr></table>
| + | \begin{equation*} | F ( 2 x ) | \leq c \sigma ( x ) , | A ( x , y ) | \leq c \sigma \left( \frac { x + y } { 2 } \right) , \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060168.png" /></td> </tr></table>
| + | \begin{equation*} \left| \frac { \partial A ( x , y ) } { \partial x } + \frac { 1 } { 4 } q \left( \frac { x + y } { 2 } \right) \right| \leq c \sigma ( x ) \sigma \left( \frac { x + y } { 2 } \right) , \left| \frac { \partial A ( x , y ) } { \partial y } + \frac { 1 } { 4 } q ( \frac { x + y } { 2 } ) \right| \leq c \sigma ( x ) \sigma \left( \frac { x + y } { 2 } \right), \end{equation*} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060169.png" /> is a constant. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060170.png" /> solves the Volterra-type equation | + | where $c > 0$ is a constant. The function $A ( x , y )$ solves the Volterra-type equation |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060171.png" /></td> </tr></table>
| + | \begin{equation*} A ( x , y ) = \frac { 1 } { 2 } \int _ { ( x + y ) / 2 } ^ { \infty } q ( t ) d t + \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060172.png" /></td> </tr></table>
| + | \begin{equation*} + \int _ { \frac { x + y } { 2 } } ^ { \infty } d s \int _ { 0 } ^ { \frac { y - x } { 2 } } q ( s - t ) A ( s - t , s + t ) d t. \end{equation*} |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060173.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060174.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060175.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060176.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060177.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060178.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060179.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060180.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060181.png" />. Since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060182.png" />, it follows that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060183.png" /> is an [[Entire function|entire function]] of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060184.png" /> and type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060185.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060186.png" /> is meromorphic on the whole complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060187.png" />-plane (cf. also [[Meromorphic function|Meromorphic function]]). | + | If $q \in L _ { 1 , 1} $ and $q ( x ) = 0$ for $x > a$, then $A ( x , y ) = 0$ for $y \geq x \geq a$, $F ( x ) = 0$ for $x = 2 a$, and $A ( y ) : = A ( 0 , y ) = 0$ for $y \geq 2 a$. Since $f ( k ) = 1 + \int _ { 0 } ^ { \infty } A ( y ) e ^ { i k y } d y$, it follows that $f ( k )$ is an [[Entire function|entire function]] of order $1$ and type $\leq 2 a$, and $S ( k ) = f ( - k ) / f ( k )$ is meromorphic on the whole complex $k$-plane (cf. also [[Meromorphic function|Meromorphic function]]). |
| | | | |
| − | Conversely, if the scattering data <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060188.png" /> correspond to a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060189.png" /> (necessary and sufficient conditions for this were given above) and generate (by solving the Riemann problem mentioned above) the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060190.png" /> which is an entire function of exponential type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060191.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060192.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060193.png" />, (see [[#References|[a6]]]). | + | Conversely, if the scattering data $\mathcal{S}$ correspond to a $q \in L _ { 1 , 1} $ (necessary and sufficient conditions for this were given above) and generate (by solving the Riemann problem mentioned above) the function $f ( k )$ which is an entire function of exponential type $\leq 2 a$, then $q ( x ) = 0$ for $x > a$, (see [[#References|[a6]]]). |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Chadan, P. Sabatier, "Inverse problems in quantum scattering theory" , Springer (1989)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Krein, "Theory of accelerants and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060194.png" />-matrices of canonical differential systems" ''Dokl. Akad. Nauk. USSR'' , '''III''' : 6 (1956) pp. 1167–1170 (In Russian)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> B. Levitan, "Inverse Sturm–Liouville problems" , VNU Press (1987)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> V. Marchenko, "Stability in the inverse problem of scattering theory" ''Mat. Sb.'' , '''77''' (1968) pp. 139–162 (In Russian)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> V. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> A.G. Ramm, "Multidimensional inverse scattering problems" , Longman/Wiley (1992)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> A.G. Ramm, "Recovery of the potential from I-function" ''Math. Rept. Acad. Sci. Canada'' , '''9''' (1987) pp. 177–182</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> A.G. Ramm, "Recovery of compactly supported spherically symmetric potentials from the phase shift of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060195.png" />-wave" A.G. Ramm (ed.) , ''Spectral and Scattering Theory'' , Plenum (1998) pp. 111–130</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> A.G. Ramm, "Compactly supported spherically symmetric potentials are uniquely determined by the phase shift of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i130/i130060/i130060196.png" />-wave" ''Phys. Lett. A'' , '''242''' : 4–5 (1998) pp. 215–219</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> A.G. Ramm, "Recovery of a quarkonium system from experimental data" ''J. Phys. A'' , '''31''' : 15 (1998) pp. L295–L299</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> A.G. Ramm, "Inverse scattering problem with part of the fixed-energy phase shifts" ''Comm. Math. Phys.'' , '''207''' : 1 (1999) pp. 231–247</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> A.G. Ramm, "Property C for ODE and applications to inverse scattering" ''Z. Angew. Anal.'' , '''18''' : 2 (1999) pp. 331–348</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> A.G. Ramm, "Property C for ODE and applications to inverse problems" A.G. Ramm (ed.) P.N. Shivakumar (ed.) A.V. Strauss (ed.) , ''Operator Theory and Applications'' , ''Fields Inst. Commun.'' , '''25''' , Amer. Math. Soc. (2000) pp. 15–75</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> A.G. Ramm, W. Scheid, "An approximate method for solving inverse scattering problem with fixed-energy data" ''J. Inverse Ill-Posed Probl.'' , '''7''' : 6 (1999) pp. 561–571</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> A.G. Ramm, "Krein's method in inverse scattering" , ''Operator Theory and Applications'' , Amer. Math. Soc. (2000) pp. 441–456</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> K. Chadan, P. Sabatier, "Inverse problems in quantum scattering theory" , Springer (1989)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> M. Krein, "Theory of accelerants and $S$-matrices of canonical differential systems" ''Dokl. Akad. Nauk. USSR'' , '''III''' : 6 (1956) pp. 1167–1170 (In Russian)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> B. Levitan, "Inverse Sturm–Liouville problems" , VNU Press (1987)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> V. Marchenko, "Stability in the inverse problem of scattering theory" ''Mat. Sb.'' , '''77''' (1968) pp. 139–162 (In Russian)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> V. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> A.G. Ramm, "Multidimensional inverse scattering problems" , Longman/Wiley (1992)</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> A.G. Ramm, "Recovery of the potential from I-function" ''Math. Rept. Acad. Sci. Canada'' , '''9''' (1987) pp. 177–182</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> A.G. Ramm, "Recovery of compactly supported spherically symmetric potentials from the phase shift of $s$-wave" A.G. Ramm (ed.) , ''Spectral and Scattering Theory'' , Plenum (1998) pp. 111–130</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> A.G. Ramm, "Compactly supported spherically symmetric potentials are uniquely determined by the phase shift of $s$-wave" ''Phys. Lett. A'' , '''242''' : 4–5 (1998) pp. 215–219</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> A.G. Ramm, "Recovery of a quarkonium system from experimental data" ''J. Phys. A'' , '''31''' : 15 (1998) pp. L295–L299</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> A.G. Ramm, "Inverse scattering problem with part of the fixed-energy phase shifts" ''Comm. Math. Phys.'' , '''207''' : 1 (1999) pp. 231–247</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> A.G. Ramm, "Property C for ODE and applications to inverse scattering" ''Z. Angew. Anal.'' , '''18''' : 2 (1999) pp. 331–348</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> A.G. Ramm, "Property C for ODE and applications to inverse problems" A.G. Ramm (ed.) P.N. Shivakumar (ed.) A.V. Strauss (ed.) , ''Operator Theory and Applications'' , ''Fields Inst. Commun.'' , '''25''' , Amer. Math. Soc. (2000) pp. 15–75</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> A.G. Ramm, W. Scheid, "An approximate method for solving inverse scattering problem with fixed-energy data" ''J. Inverse Ill-Posed Probl.'' , '''7''' : 6 (1999) pp. 561–571</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> A.G. Ramm, "Krein's method in inverse scattering" , ''Operator Theory and Applications'' , Amer. Math. Soc. (2000) pp. 441–456</td></tr></table> |
The direct scattering problem on the half-axis consists of finding the solution $u ( x , k )$ to the problem
\begin{equation} \tag{a1} u ^ { \prime \prime } + k ^ { 2 } u - q ( x ) u = 0 , x > 0, \end{equation}
\begin{equation} \tag{a2} u ( 0 , k ) = 0 \end{equation}
\begin{equation} \tag{a3} u ( x , k ) = e ^ { i \delta } \operatorname { sin } ( k x + \delta ) + o ( 1 ) , \quad \text { as } x \rightarrow \infty. \end{equation}
Here, $\delta = \delta ( k )$ is to be determined. The function $\delta = \delta ( k )$ is called the phase shift. The coefficient $q ( x )$ is called the scattering potential. It is assumed to be a real-valued function in the class
\begin{equation*} L _ { 1,1 } : = \left\{ q : \int _ { 0 } ^ { \infty } x | q ( x ) | d x < \infty , q = \overline { q } \right\}, \end{equation*}
where the bar stands for complex conjugation. The solution $f ( x , k )$ to (a1) which satisfies the relation $f ( x , k ) = e ^ { i k x } + o ( 1 )$, as $x \rightarrow + \infty$, is called the Jost solution. The function $f ( 0 , k ) : = f ( k )$ is called the Jost function. One has
\begin{equation*} f ( k ) = | f ( k ) | e ^ { - i \delta ( k ) }, \end{equation*}
\begin{equation*} \delta ( - k ) = - \delta ( k ) , k \in \mathbf{R} , \quad \delta ( \infty ) = 0. \end{equation*}
If $q \in L _ { 1 , 1} $, then $f ( x , k )$ exists and is unique, $f ( k )$ is analytic in $\mathbf{C} _ { + } : = \{ k : \operatorname { Im } k > 0 \}$ and has at most finitely many zeros in $\mathbf{C} _ { + }$, all of which are simple and of the form $i k_j$, $k_ j > 0$, $1 \leq j \leq J$. The numbers $- k _ { j } ^ { 2 }$ are the eigenvalues of the self-adjoint operator
\begin{equation*} l : = - \frac { d ^ { 2 } } { d x ^ { 2 } } + q ( x ), \end{equation*}
which is determined by the Dirichlet boundary condition at $x = 0$ in the Hilbert space $L ^ { 2 } ( \mathbf{R} _ { + } )$, $\mathbf{R} _ { + } : = [ 0 , \infty )$ (cf. also Dirichlet boundary conditions). In physics, $- k ^ { 2}j $ are called the bound states. The positive numbers $s _ { j } : = \| f ( x , i k _ { j } ) \| ^ { - 2 _{L ^ { 2} ( \mathbf{R} _ { + } )}}$ are called the norming constants. The function $S ( k ) = f ( - k ) / f ( k ) = e ^ { 2 i \delta ( k ) }$ is called the $S$-matrix (cf. Scattering matrix). The triple 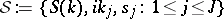 is called the scattering data.
is called the scattering data.
The inverse scattering problem consists of finding $q ( x )$ given $\mathcal{S}$.
The point $k = 0$ can also be a zero of $f ( k )$. It is called a resonance at $k = 0$. If $f ( 0 ) = 0$, then $f ^ { \prime } ( 0 ) \neq 0$. The basic results of inverse scattering theory are (see [a5], [a6]):
1) The uniqueness theorem: $\mathcal{S} \Rightarrow q$; that is, the scattering data determine $q \in L _ { 1 , 1} $ uniquely.
2) The reconstruction theorem: If $\mathcal{S}$, corresponding to a $q \in L _ { 1 , 1} $, is given, then $q ( x )$ can be reconstructed by the Marchenko method, as follows:'
| 1 | Calculate
\begin{equation*} F ( x ) : = \sum _ { j = 1 } ^ { J } s _ { j } e ^ { - k _ { j } x } + \frac { 1 } { 2 \pi } \int _ { - \infty } ^ { \infty } [ 1 - S ( k ) ] e ^ { i k x } d k. \end{equation*}
| | 2 | Solve the following equation for $A ( x , y )$:
\begin{equation} \tag{a4} A ( x , y ) + F ( x , y ) + \int _ { x } ^ { \infty } A ( x , s ) F ( s + y ) d s = 0, \end{equation}
\begin{equation*} y \geq x \geq 0. \end{equation*}
This equation is uniquely solvable and is called the Marchenko equatio. | | 3 | Calculate $q ( x ) = - 2 d A ( x , x ) / d x$. |
|
3) The characterization theorem: For $\mathcal{S}$ to be the scattering data corresponding to a $q \in L _ { 1 , 1} $ it is necessary and sufficient that the following conditions hold:
i) $\overline { S ( k ) } = S ( - k ) = S ^ { - 1 } ( k )$, $k \in {\bf R}_+$; $S ( \infty ) = 1$, $k_ j > 0$, $s _ { j } > 0$, $1 \leq j \leq J$;
ii) $\operatorname {ind} S ( k ) = - \kappa$, $\kappa = 2 J$ or $\kappa = 2 J + 1$;
iii) $\| F ( x ) \| _ { L^{\infty} ( \mathbf{R} _ { + } ) } + \| F ( x ) \| _ { L ^ { 1 } ( \mathbf{R} _ { + } ) } +$
\begin{equation*} + \| x F ^ { \prime } ( x ) \| _ { L ^ { 1 } ( \mathbf{R} _ { + } ) } < \infty. \end{equation*}
Here, $\operatorname{ ind } S ( k ) : = ( 1 / 2 \pi ) \int _ { - \infty } ^ { \infty } d \operatorname { ln } S ( k )$.
Note that $\kappa = 2 J$ if $f ( 0 ) \neq 0$, and $\kappa = 2 J + 1$ if $f ( 0 ) = 0$. The mapping $T : q \rightarrow \mathcal{S}$ is a homeomorphism between $L _ { 1 , 1}$ and the space of the scattering data equipped with the norm $\| \mathcal{S} \| : = \int _ { 0 } ^ { \infty } ( 1 + x ) | F ^ { \prime } ( x ) | d x$ (see [a4], [a5] [a6]).
One can prove (see [a6], [a13]) the diagram
\begin{equation*} \delta \Leftrightarrow F \Leftrightarrow A \Leftrightarrow q, \end{equation*}
each step of which is invertible. Here, $F = F ( x )$ and $A = A ( x , y )$ are defined above. This result guarantees, in particular, that the potential recovered by the Marchenko method generates the original scattering data (provided that $q \in L _ { 1 , 1} $ or $\mathcal{S}$ satisfies the characterization conditions).
Other methods for solving the inverse scattering problem on the half-axis are based on the solution of the inverse problem of recovery of $q ( x )$ from the spectral function $\rho : = \rho ( \lambda )$ ($\mathcal{S} \Rightarrow \rho \Rightarrow q$) and the Krein method ([a1], [a3], [a5] [a6], [a15]).
The scattering data are in one-to-one correspondence with the spectral function [a6] [a7], [a13]. Recovery of $q ( x )$ given the spectral function is discussed in [a1], [a3], [a5], [a6].
The original work of M.G. Krein [a2] and its review in [a1] do not contain proofs. A detailed presentation of Krein's theory with complete proofs is given in [a15] for the first time. Also, a proof of consistency of Krein's method is given in [a15]. In [a2] (and in [a1]) there is no discussion of the consistency of Krein's method. By the consistency of an inversion method one means a proof of the implication $q \Rightarrow \mathcal{S}$ (the reconstructed potential generates the data from which it was reconstructed).
Below, Krein's method is described under the simplifying assumption $\kappa = 0$ (no bound states and no resonance at $k = 0$). The general case is treated in [a15].'
| 1 | Given $S ( k ) = e ^ { 2 i \delta ( k ) }$, $\operatorname{ind} S ( k ) = 0$, $\delta ( \infty ) = 0$, one finds $\delta ( k )$, then calculates
\begin{equation*} g ( t ) : = - \frac { 2 } { \pi } \int _ { 0 } ^ { \infty } \delta ( k ) \operatorname { sin } ( k t ) d k, \end{equation*}
\begin{equation*} f ( k ) = \operatorname { exp } ( \int _ { 0 } ^ { \infty } g ( t ) e ^ { i k t } d t ), \end{equation*}
and
\begin{equation*} H ( t ) : = - \frac { 1 } { 2 \pi } \int _ { - \infty } ^ { \infty } \left( | f ( k ) | ^ { - 2 } - 1 \right) e ^ { - i k t } d k. \end{equation*}
| | 2 | Given $H ( t )$, one solves the equation
\begin{equation*} ( I + H _ { x } ) \Gamma _ { x } : = \Gamma _ { x } ( t , s ) + \int _ { 0 } ^ { x } H ( t - u ) \Gamma _ { x } ( u , s ) d u = H ( t - s ) ,\, 0 \leq t , s \leq x, \end{equation*}
for $\Gamma _ { x } ( t , s )$ and finds $\Gamma _ { 2 x } ( 2 x , 0 )$, $0 \leq x < \infty$. | | $A ( x ) = 2 \Gamma _ { 2 x } ( 2 x , 0 )$, and calculates $q ( x ) = A ^ { 2 } ( x ) + A ^ { \prime } ( x )$. Alternatively,
\begin{equation*} q ( x ) = 2 \frac { d } { d x } [ \Gamma _ { 2 x } ( 2 x , 0 ) - \Gamma _ { 2 x } ( 0,0 ) ]. \end{equation*}
|
|
In Step 1, one can find $f ( k )$ by a different method: Solve the Riemann problem
\begin{equation} \tag{a5} \varphi_{+} ( k ) = S ( - k ) \varphi _ { - } ( k ), \end{equation}
\begin{equation*} k \in \mathbf{R} , \varphi _ { \pm } ( \infty ) = 1. \end{equation*}
If $\operatorname{ind} S ( k ) = 0$, this problem has the unique solution $\{ \varphi_+ ( k ) , \varphi_- ( k ) \}$. One has $\varphi _ { + } ( k ) = f ( k )$, $\varphi_{-} ( k ) = f ( - k )$.
Note that the data $\mathcal{S}$ allow one to find a unique $f ( k )$ by solving the Riemann problem (a5) with the additional conditions: $\varphi_{+} ( k )$ has $J$ simple zeros at the points $i k_j$ if $\kappa = - 2 J$ and, if $\kappa = - 2 J - 1$, $\varphi_{+} ( k )$ has, in addition, a simple zero at $k = 0$. Thus, the data $\mathcal{S}$ is equivalent to the data $\{ f ( k ) , s _j 1 \leq j \leq J \}$.
An inverse problem of recovery of $q ( x )$ from incomplete scattering data but with an a priori assumption that $q ( x )$ has compact support is investigated in [a8] [a9]. It is proved that if $q \in L _ { 1 , 1} $ is compactly supported and if $\delta ( k )$ is known for a sequence $k = k _ { n } > 0$ which has a finite limit point inside $( 0 , \infty )$, then $q ( x )$ is determined uniquely. An algorithm for finding a compactly supported $q ( x )$ from $\delta ( k )$ (that is, from $\mathcal{S} ( k )$) known for all $k > 0$ is given in [a8]. A uniqueness theorem for the problem of finding a compactly supported $q ( x )$ from the knowledge of $f ^ { \prime } ( 0 , k )$, $\forall k > 0$, is proved in [a13].
In [a7], [a12] an algorithm for recovery of $q ( x )$ from the $I$-function is given, where the $I$-function is identical with the Weyl function.
For $q \in L _ { 1 , 1} $ to belong to $L ^ { 2 } ( \mathbf{R} _ { + } )$ it is necessary and sufficient [a6] that
\begin{equation} \tag{a6} k \left[ 1 - S ( k ) + \frac { Q } { i k } \right] \in L ^ { 2 } ( \mathbf{R} ), \end{equation}
where
\begin{equation*} Q : = \int _ { 0 } ^ { \infty } q ( t ) d t = - 2 i \operatorname { lim } _ { k \rightarrow \infty } \{ k [ f ( k ) - 1 ] \}. \end{equation*}
If $q ( x ) \in L _ { 1,1 } \cap L ^ { 2 } ( \mathbf{R} _ { + } )$, $q = 0$ for $x \geq a$, is compactly supported, then $f ( k )$ is an entire function of exponential type $\leq 2 a$. Its zeros in $\mathbf{C} _ { - } : = \{ k : \operatorname { Im } k < 0 \}$ are called resonances.
If $q ( x ) \not\equiv 0$, $\int _ { 0 } ^ { \infty } x ^ { n } | q ( x ) | d x = o ( n ^ { b n } )$, $0 \leq b < 1$, then there are infinitely many resonances [a6].
There exists a $q ( x ) \in C _ { 0 } ^ { \infty } ( \mathbf{R} + )$, $q ( x ) = 0$ for $x \geq \epsilon$, where $\epsilon > 0$ is arbitrary small, which generates infinitely many purely imaginary resonances [a6].
If $q ( x ) \in L _ { 1,1 }$, $q ( x ) = 0$ for $x \geq a$ and $q ( x )$ does not change sign in an interval $( a - \delta , a )$, where $\delta > 0$ is arbitrarily small, then $q ( x )$ generates only finitely many purely imaginary resonances (a6).
If $q \in L _ { 1 , 1} $, then the following estimate (see [a5]) is useful:
\begin{equation*} \left| F ^ { \prime } ( 2 x ) - \frac { q ( x ) } { 4 } + \frac { 1 } { 4 } \left( \int _ { x } ^ { \infty } q ( t ) d t \right)^2 \right| \leq c \sigma ^ { 2 } ( x ), \end{equation*}
\begin{equation*} \sigma ( x ) : = \int _ { x } ^ { \infty } | q ( t ) | d t. \end{equation*}
The Jost solution $f ( x , k )$ can be written as $f ( x , k ) = e ^ { i k x } + \int _ { x } ^ { \infty } A ( x , y ) e ^ { i k y } d y$, where $A ( x , y )$ is the kernel of the transformation operator. If $q \in L _ { 1 , 1} $, then
\begin{equation*} | F ( 2 x ) + A ( x , x ) | \leq c \sigma ( x ), \end{equation*}
\begin{equation*} | F ( 2 x ) | \leq c \sigma ( x ) , | A ( x , y ) | \leq c \sigma \left( \frac { x + y } { 2 } \right) , \end{equation*}
\begin{equation*} \left| \frac { \partial A ( x , y ) } { \partial x } + \frac { 1 } { 4 } q \left( \frac { x + y } { 2 } \right) \right| \leq c \sigma ( x ) \sigma \left( \frac { x + y } { 2 } \right) , \left| \frac { \partial A ( x , y ) } { \partial y } + \frac { 1 } { 4 } q ( \frac { x + y } { 2 } ) \right| \leq c \sigma ( x ) \sigma \left( \frac { x + y } { 2 } \right), \end{equation*}
where $c > 0$ is a constant. The function $A ( x , y )$ solves the Volterra-type equation
\begin{equation*} A ( x , y ) = \frac { 1 } { 2 } \int _ { ( x + y ) / 2 } ^ { \infty } q ( t ) d t + \end{equation*}
\begin{equation*} + \int _ { \frac { x + y } { 2 } } ^ { \infty } d s \int _ { 0 } ^ { \frac { y - x } { 2 } } q ( s - t ) A ( s - t , s + t ) d t. \end{equation*}
If $q \in L _ { 1 , 1} $ and $q ( x ) = 0$ for $x > a$, then $A ( x , y ) = 0$ for $y \geq x \geq a$, $F ( x ) = 0$ for $x = 2 a$, and $A ( y ) : = A ( 0 , y ) = 0$ for $y \geq 2 a$. Since $f ( k ) = 1 + \int _ { 0 } ^ { \infty } A ( y ) e ^ { i k y } d y$, it follows that $f ( k )$ is an entire function of order $1$ and type $\leq 2 a$, and $S ( k ) = f ( - k ) / f ( k )$ is meromorphic on the whole complex $k$-plane (cf. also Meromorphic function).
Conversely, if the scattering data $\mathcal{S}$ correspond to a $q \in L _ { 1 , 1} $ (necessary and sufficient conditions for this were given above) and generate (by solving the Riemann problem mentioned above) the function $f ( k )$ which is an entire function of exponential type $\leq 2 a$, then $q ( x ) = 0$ for $x > a$, (see [a6]).
References
| [a1] | K. Chadan, P. Sabatier, "Inverse problems in quantum scattering theory" , Springer (1989) |
| [a2] | M. Krein, "Theory of accelerants and $S$-matrices of canonical differential systems" Dokl. Akad. Nauk. USSR , III : 6 (1956) pp. 1167–1170 (In Russian) |
| [a3] | B. Levitan, "Inverse Sturm–Liouville problems" , VNU Press (1987) |
| [a4] | V. Marchenko, "Stability in the inverse problem of scattering theory" Mat. Sb. , 77 (1968) pp. 139–162 (In Russian) |
| [a5] | V. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986) |
| [a6] | A.G. Ramm, "Multidimensional inverse scattering problems" , Longman/Wiley (1992) |
| [a7] | A.G. Ramm, "Recovery of the potential from I-function" Math. Rept. Acad. Sci. Canada , 9 (1987) pp. 177–182 |
| [a8] | A.G. Ramm, "Recovery of compactly supported spherically symmetric potentials from the phase shift of $s$-wave" A.G. Ramm (ed.) , Spectral and Scattering Theory , Plenum (1998) pp. 111–130 |
| [a9] | A.G. Ramm, "Compactly supported spherically symmetric potentials are uniquely determined by the phase shift of $s$-wave" Phys. Lett. A , 242 : 4–5 (1998) pp. 215–219 |
| [a10] | A.G. Ramm, "Recovery of a quarkonium system from experimental data" J. Phys. A , 31 : 15 (1998) pp. L295–L299 |
| [a11] | A.G. Ramm, "Inverse scattering problem with part of the fixed-energy phase shifts" Comm. Math. Phys. , 207 : 1 (1999) pp. 231–247 |
| [a12] | A.G. Ramm, "Property C for ODE and applications to inverse scattering" Z. Angew. Anal. , 18 : 2 (1999) pp. 331–348 |
| [a13] | A.G. Ramm, "Property C for ODE and applications to inverse problems" A.G. Ramm (ed.) P.N. Shivakumar (ed.) A.V. Strauss (ed.) , Operator Theory and Applications , Fields Inst. Commun. , 25 , Amer. Math. Soc. (2000) pp. 15–75 |
| [a14] | A.G. Ramm, W. Scheid, "An approximate method for solving inverse scattering problem with fixed-energy data" J. Inverse Ill-Posed Probl. , 7 : 6 (1999) pp. 561–571 |
| [a15] | A.G. Ramm, "Krein's method in inverse scattering" , Operator Theory and Applications , Amer. Math. Soc. (2000) pp. 441–456 |
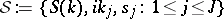 is called the scattering data.
is called the scattering data.