|
|
| Line 1: |
Line 1: |
| | + | {{TEX|done}} |
| | ''planar ternary ring'' | | ''planar ternary ring'' |
| | | | |
| − | A set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t0924301.png" /> with two special elements, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t0924302.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t0924303.png" />, provided with a ternary operation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t0924304.png" /> satisfying: | + | A set $R$ with two special elements, $0$ and $1$, provided with a ternary operation $T$ satisfying: |
| | | | |
| − | A) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t0924305.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t0924306.png" />; | + | A) $T(a,0,c)=T(0,b,c)=c$ for all $a,b,c\in R$; |
| | | | |
| − | B) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t0924307.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t0924308.png" />; | + | B) $T(a,1,0)=T(1,a,0)=a$ for all $a\in R$; |
| | | | |
| − | C) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t0924309.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243010.png" />, then there is a unique <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243011.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243012.png" />; | + | C) if $a,b,c,d\in R$, $a\neq c$, then there is a unique $x\in R$ such that $T(x,a,b)=T(x,c,d)$; |
| | | | |
| − | D) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243013.png" />, then there is a unique <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243014.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243015.png" />; | + | D) if $a,b,c\in R$, then there is a unique $x\in R$ such that $T(a,b,x)=c$; |
| | | | |
| − | E) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243016.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243017.png" />, then there are unique <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243018.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243019.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243020.png" />. | + | E) if $a,b,c,d\in R$, $a\neq c$, then there are unique $x,y\in R$ such that $T(a,x,y)=b$ and $T(c,x,y)=d$. |
| | | | |
| − | Ternary fields were introduced in [[#References|[a1]]] for the purpose of coordinatizing arbitrary, not necessarily Desarguesian, projective planes (cf. [[Desargues assumption|Desargues assumption]]; [[Desargues geometry|Desargues geometry]]; [[Projective plane|Projective plane]]). Slight variations of the original definition were given in [[#References|[a2]]] and [[#References|[a3]]], which is followed here. Given a projective plane, fix four points in [[General position|general position]]: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243021.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243022.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243024.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243026.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243027.png" />. For the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243028.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243029.png" /> one chooses coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243030.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243031.png" /> running over a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243032.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243033.png" />, assigning <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243034.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243035.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243036.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243037.png" />. The projection of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243038.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243039.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243040.png" /> is given coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243041.png" />, and then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243042.png" /> (see Fig.a1). The points on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243043.png" /> get one coordinate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243044.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243045.png" />, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243046.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243047.png" /> is an extra symbol <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243048.png" />, and the lines are coordinatized by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243049.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243050.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243051.png" />, as in Fig.a2. | + | Ternary fields were introduced in [[#References|[a1]]] for the purpose of coordinatizing arbitrary, not necessarily Desarguesian, projective planes (cf. [[Desargues assumption|Desargues assumption]]; [[Desargues geometry|Desargues geometry]]; [[Projective plane|Projective plane]]). Slight variations of the original definition were given in [[#References|[a2]]] and [[#References|[a3]]], which is followed here. Given a projective plane, fix four points in [[General position|general position]]: $O$, $X$, $Y$, $I$, and let $A=YI\cap OX$, $B=XI\cap OY$ and $J=AB\cap XY$. For the points $\neq Y$ of $OY$ one chooses coordinates $(0,y)$ with $y$ running over a set $R$ and $0\in R$, assigning $(0,0)$ to $O$ and $(0,1)$ to $B$. The projection of $(0,x)$ from $J$ on $OX$ is given coordinates $(x,0)$, and then $Y(x,0)\cap X(0,y)=(x,y)$ (see Fig.a1). The points on $XY$ get one coordinate $(m)$, with $m\in R$, or $(\infty)$, where $\infty$ is an extra symbol $\notin R$, and the lines are coordinatized by $[m,k]$, $[b]$ or $[\infty]$, as in Fig.a2. |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/t092430a.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/t092430a.gif" /> |
| Line 23: |
Line 24: |
| | Figure: t092430b | | Figure: t092430b |
| | | | |
| − | The ternary operation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243052.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243053.png" /> is defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243054.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243055.png" /> lies on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243056.png" />. The properties A)–E) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243057.png" /> are then consequences of the axioms for a projective plane. Conversely, any ternary field coordinatizes a projective plane. It may happen that different ternary fields coordinatize the same plane, for a different choice of basis points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243058.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243060.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243061.png" />. | + | The ternary operation $T$ on $R$ is defined by $T(a,b,c)=k$ if and only if $(b,c)$ lies on $[a,k]$. The properties A)–E) for $T$ are then consequences of the axioms for a projective plane. Conversely, any ternary field coordinatizes a projective plane. It may happen that different ternary fields coordinatize the same plane, for a different choice of basis points $O$, $X$, $Y$, $I$. |
| | | | |
| − | In case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243062.png" /> is finite, C) and D) are equivalent to D) and E); further, C) is then a consequence of D) and the existence of at most one <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243063.png" /> as in C). | + | In case $R$ is finite, C) and D) are equivalent to D) and E); further, C) is then a consequence of D) and the existence of at most one $x$ as in C). |
| | | | |
| − | On a ternary field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243064.png" />, addition is defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243065.png" />; with this operation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243066.png" /> is a [[Loop|loop]] with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243067.png" /> as neutral element. Multiplication is defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243068.png" />; this makes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243069.png" /> a loop with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243070.png" /> as neutral element. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243071.png" /> is said to be linear if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243072.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243073.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243074.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243075.png" />. Linearity is equivalent to a very weak Desargues-type condition on triangles which are in perspective from the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243076.png" /> (cf. [[Configuration|Configuration]], in particular Desarguesian configuration, and also [[Desargues assumption|Desargues assumption]]). Other algebraic properties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243077.png" />, such as associativity of addition or multiplication and left or right distributivity, can also be translated into certain Desargues-type conditions. In particular, a translation plane with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243078.png" /> as translation line, i.e., a plane in which the group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243079.png" />-translations is transitive on the points not on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243080.png" />, is coordinatized by a (left) quasi-field, which is a linear ternary field with associative addition satisfying the left distributive law <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092430/t09243081.png" />. | + | On a ternary field $(R,T)$, addition is defined by $a+b=T(1,a,b)$; with this operation $R$ is a [[Loop|loop]] with $=$ as neutral element. Multiplication is defined by $ab=T(a,b,0)$; this makes $R\setminus\{0\}$ a loop with $1$ as neutral element. $(R,T)$ is said to be linear if $T(a,b,c)=ab+c$ for all $a$, $b$, $c$. Linearity is equivalent to a very weak Desargues-type condition on triangles which are in perspective from the point $(\infty)$ (cf. [[Configuration|Configuration]], in particular Desarguesian configuration, and also [[Desargues assumption|Desargues assumption]]). Other algebraic properties of $(R,T)$, such as associativity of addition or multiplication and left or right distributivity, can also be translated into certain Desargues-type conditions. In particular, a translation plane with $XY$ as translation line, i.e., a plane in which the group of $XY$-translations is transitive on the points not on $XY$, is coordinatized by a (left) quasi-field, which is a linear ternary field with associative addition satisfying the left distributive law $a(b+c)=ab+ac$. |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Hall, "Projective planes" ''Trans. Amer. Math. Soc.'' , '''54''' (1943) pp. 229–277</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G. Pickert, "Projective Ebenen" , Springer (1975)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D.R. Hughes, F.C. Piper, "Projective planes" , Springer (1973)</TD></TR></table> | | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Hall, "Projective planes" ''Trans. Amer. Math. Soc.'' , '''54''' (1943) pp. 229–277</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G. Pickert, "Projective Ebenen" , Springer (1975)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D.R. Hughes, F.C. Piper, "Projective planes" , Springer (1973)</TD></TR></table> |
planar ternary ring
A set $R$ with two special elements, $0$ and $1$, provided with a ternary operation $T$ satisfying:
A) $T(a,0,c)=T(0,b,c)=c$ for all $a,b,c\in R$;
B) $T(a,1,0)=T(1,a,0)=a$ for all $a\in R$;
C) if $a,b,c,d\in R$, $a\neq c$, then there is a unique $x\in R$ such that $T(x,a,b)=T(x,c,d)$;
D) if $a,b,c\in R$, then there is a unique $x\in R$ such that $T(a,b,x)=c$;
E) if $a,b,c,d\in R$, $a\neq c$, then there are unique $x,y\in R$ such that $T(a,x,y)=b$ and $T(c,x,y)=d$.
Ternary fields were introduced in [a1] for the purpose of coordinatizing arbitrary, not necessarily Desarguesian, projective planes (cf. Desargues assumption; Desargues geometry; Projective plane). Slight variations of the original definition were given in [a2] and [a3], which is followed here. Given a projective plane, fix four points in general position: $O$, $X$, $Y$, $I$, and let $A=YI\cap OX$, $B=XI\cap OY$ and $J=AB\cap XY$. For the points $\neq Y$ of $OY$ one chooses coordinates $(0,y)$ with $y$ running over a set $R$ and $0\in R$, assigning $(0,0)$ to $O$ and $(0,1)$ to $B$. The projection of $(0,x)$ from $J$ on $OX$ is given coordinates $(x,0)$, and then $Y(x,0)\cap X(0,y)=(x,y)$ (see Fig.a1). The points on $XY$ get one coordinate $(m)$, with $m\in R$, or $(\infty)$, where $\infty$ is an extra symbol $\notin R$, and the lines are coordinatized by $[m,k]$, $[b]$ or $[\infty]$, as in Fig.a2.
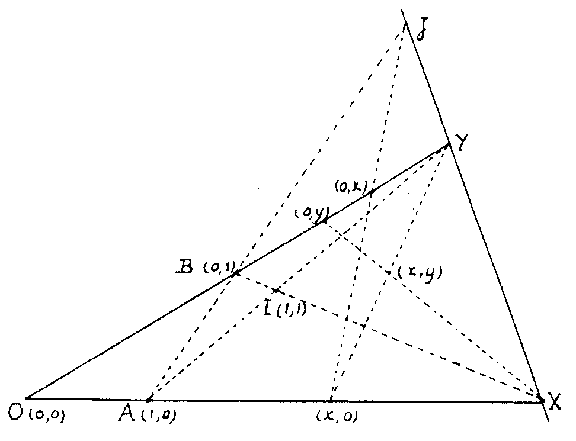
Figure: t092430a
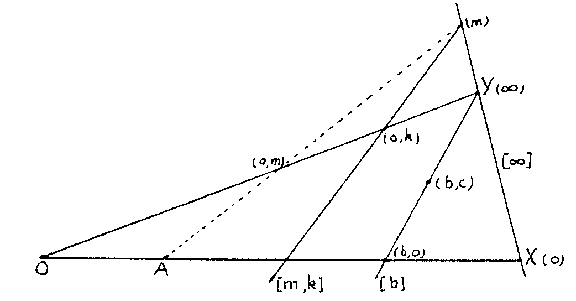
Figure: t092430b
The ternary operation $T$ on $R$ is defined by $T(a,b,c)=k$ if and only if $(b,c)$ lies on $[a,k]$. The properties A)–E) for $T$ are then consequences of the axioms for a projective plane. Conversely, any ternary field coordinatizes a projective plane. It may happen that different ternary fields coordinatize the same plane, for a different choice of basis points $O$, $X$, $Y$, $I$.
In case $R$ is finite, C) and D) are equivalent to D) and E); further, C) is then a consequence of D) and the existence of at most one $x$ as in C).
On a ternary field $(R,T)$, addition is defined by $a+b=T(1,a,b)$; with this operation $R$ is a loop with $=$ as neutral element. Multiplication is defined by $ab=T(a,b,0)$; this makes $R\setminus\{0\}$ a loop with $1$ as neutral element. $(R,T)$ is said to be linear if $T(a,b,c)=ab+c$ for all $a$, $b$, $c$. Linearity is equivalent to a very weak Desargues-type condition on triangles which are in perspective from the point $(\infty)$ (cf. Configuration, in particular Desarguesian configuration, and also Desargues assumption). Other algebraic properties of $(R,T)$, such as associativity of addition or multiplication and left or right distributivity, can also be translated into certain Desargues-type conditions. In particular, a translation plane with $XY$ as translation line, i.e., a plane in which the group of $XY$-translations is transitive on the points not on $XY$, is coordinatized by a (left) quasi-field, which is a linear ternary field with associative addition satisfying the left distributive law $a(b+c)=ab+ac$.
References
| [a1] | M. Hall, "Projective planes" Trans. Amer. Math. Soc. , 54 (1943) pp. 229–277 |
| [a2] | G. Pickert, "Projective Ebenen" , Springer (1975) |
| [a3] | D.R. Hughes, F.C. Piper, "Projective planes" , Springer (1973) |

