Spherical matrix distribution

A random matrix 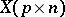(cf. also Matrix variate distribution) is said to have

a right spherical distribution if 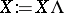for all ;

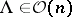a left spherical distribution if 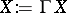for all 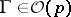; and

a spherical distribution if 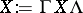for all 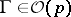and all 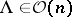. Here, 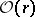denotes the class of orthogonal 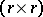-matrices (cf. also Orthogonal matrix).

Instead of saying that 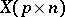"has a" (left, right) spherical distribution, one also says that 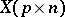itself is (left, right) spherical.

If 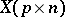is right spherical, then

a) its transpose 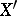is left spherical;

b) 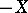is right spherical, i.e. 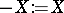; and

c) for 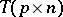, its characteristic function is of the form .

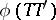The fact that 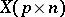is right (left) spherical with characteristic function 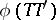, is denoted by 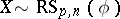(respectively, ).

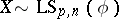Let 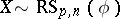. Then:

1) for a constant matrix 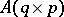, , 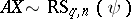where , ;

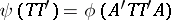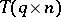2) for 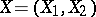, where 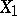is a 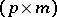-matrix, ;

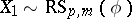3) if 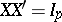, , 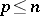then 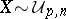, the uniform distribution on the Stiefel manifold .

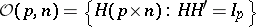The probability distribution of a right spherical matrix is fully determined by that of 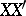. It follows that the uniform distribution is the unique right spherical distribution over 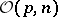. For a right spherical matrix the density need not exist in general. However, if has a density with respect to Lebesgue measure on 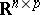, then it is of the form .

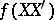Examples of spherical distributions with a density.

When 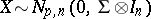, the density of 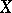is

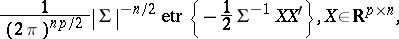with characteristic function

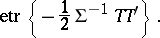Here, 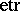is the exponential trace function:

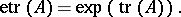When 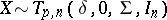, the density of 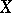is

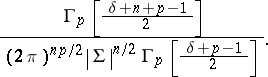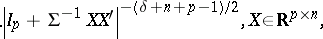with characteristic function

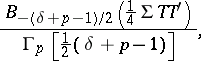where 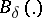is Herz's Bessel function of the second kind and of order .

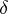If 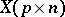is right spherical and is a fixed matrix, then the distribution of 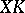depends on 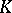only through 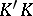. Now, if 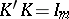, then the distribution of 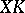is right spherical.

Let 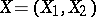, with 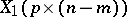, , 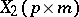and let , where , 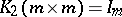. Then 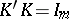, and therefore 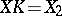is right spherical.

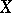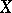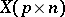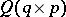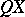If the distribution of is a mixture of right spherical distributions, then is right spherical. It follows that if , conditional on a random variable , is right spherical and is a function of , then is right spherical.

The results given above have obvious analogues for left spherical distributions.

Stochastic representation of spherical distributions.

Let . Then there exists a random matrix 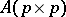such that

(a1)

where 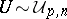is independent of .

The matrix 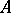in the stochastic representation (a1) is not unique. One can take it to be a lower (upper) triangular matrix with non-negative diagonal elements or a right spherical matrix with 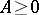. Further, if it is additionally assumed that 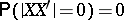, then the distribution of 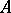is unique.

Given the assumption that 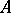is lower triangular in the above representation, one can prove that it is unique. Indeed, let 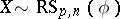and 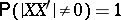. Then for 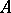, 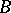lower triangular matrices with positive diagonal elements and , :

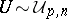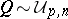i) 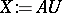and ;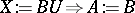

ii) 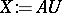and .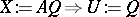

For studying the spherical distribution, singular value decomposition of the matrix 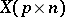provides a powerful tool. When 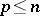, let 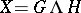, where 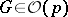, , 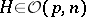, , 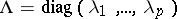and the 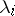are the eigenvalues of .

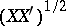If 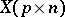, , is spherical, then

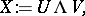(a2)

where 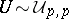, 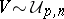and 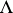are mutually independent.

If is spherical, then its characteristic function is of the form 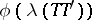, where 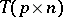, , 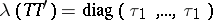and 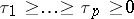are the eigenvalues of .

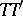From the above it follows that, if the density of a spherical matrix 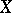exists, then it is of the form .

Let 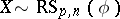. If the second-order moments of 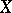exist (cf. also Moment), then

i) ;

ii) 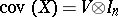, where , .

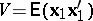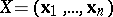Let 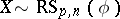with density 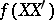. Then the density of 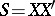, , is

Let 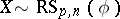with density 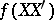. Partition 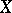as , , 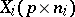, , 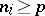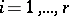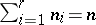. Define 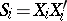, 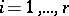. Then with probability density function

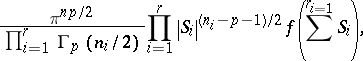The above result has been generalized further. Let 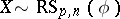with density 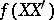, and let 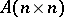be a symmetric matrix. Then

(a3)

where is the Weyl fractional integral of order 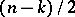(cf. also Fractional integration and differentiation), if and only if and 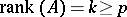. Further, let 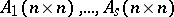be symmetric matrices. Then

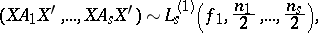(a4)

where 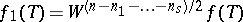, if and only if 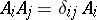, and , , .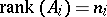

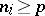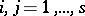References

[a1]	A.P. Dawid, "Spherical matrix distributions and multivariate model" J. R. Statist. Soc. Ser. B , 39 (1977) pp. 254–261
[a2]	K.T. Fang, Y.T. Zhang, "Generalized multivariate analysis" , Springer (1990)
[a3]	A.K. Gupta, T. Varga, "Elliptically contoured models in statistics" , Kluwer Acad. Publ. (1993)