Difference between revisions of "Dickson algebra"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 43 formulas out of 44 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 44 formulas, 43 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | Let $\mathbf{F} _ { q }$ denote the field with $q$ elements (cf. [[Finite field|Finite field]]) and $V$ an $n$-dimensional $\mathbf{F} _ { q }$-vector space (cf. also [[Vector space|Vector space]]). Let $S ( V )$ denote the [[Symmetric algebra|symmetric algebra]] generated by $V$ over $\mathbf{F} _ { q }$. Since the [[General linear group|general linear group]], $\operatorname{GL} ( V ) = \operatorname { Aut } _ { \mathbf{F} _ { q } } ( V )$, acts on $V$, there is an induced action on the algebra $S ( V )$. L.E. Dickson determined the structure of the $\operatorname{GL} ( V )$-fixed subalgebra, $S ( V ) ^ { G L ( V ) }$, now known as the Dickson algebra. In [[#References|[a5]]] (see also [[#References|[a2]]], p. 90) $S ( V ) ^ { \operatorname{GL} ( V ) }$ was shown to be a polynomial algebra of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120130/d12013015.png"/> where the $\{ c _ { n,j } \}$ are homogeneous polynomials in $S ( V )$, called the Dickson invariants (sometimes this term is used to refer to any element of the Dickson algebra), and are constructed in the following manner. Let $K$ be a field extension of $\mathbf{F} _ { q }$ which contains $V$ (cf. also [[Extension of a field|Extension of a field]]). Then the monic separable polynomial whose roots are precisely the elements of $V$ has the form | ||
| − | + | \begin{equation*} f ( X ) = X ^ { q ^ { n } } + \sum _ { i = 0 } ^ { n - 1 } ( - 1 ) ^ { n - i } c _ { n , i } X ^ { q ^ { i } } \in K [ X ]. \end{equation*} | |
| − | The corresponding algebras of invariants have been computed when | + | Suppose that $W$ is an $n$-dimensional $\mathbf{F} _ { p }$-vector space ($p$ a prime number). When $p = 2$, the cohomology algebra $H ^ { * } ( W ; \mathbf{F} _ { 2 } )$ is isomorphic to $S ( H ^ { 1 } ( W ; \mathbf{F} _ { 2 } ) )$. Therefore, over $\mathbf{F} _ { p }$ it is natural to endow $S ( V )$ with the structure of a [[Graded algebra|graded algebra]] with $V$ of dimension one if $p = 2$ and of dimension two if $p$ is odd. |
| + | |||
| + | In this topological manifestation, the Dickson algebra has proved very useful ([[#References|[a1]]], [[#References|[a4]]], [[#References|[a8]]], [[#References|[a10]]]). For example, if $\rho : W \rightarrow O _ { 2^{n} } ( \mathbf{R} )$ is the real [[Regular representation|regular representation]] of $W$ and $V = H ^ { 1 } ( W ; \mathbf{F} _ { 2 } )$, then the [[Stiefel–Whitney class|Stiefel–Whitney class]] satisfies $w _ { 2 ^ { n } - 2 ^ { i } } ( \rho ) = c _ { n , i }$ [[#References|[a7]]]. When $p$ is odd, $c _ { n , i }$ is related in a similar manner to Chern classes of the regular representation. The observation shows that the Dickson algebra becomes a graded algebra together with an action by the [[Steenrod algebra|Steenrod algebra]] of cohomology operations. In [[Algebraic topology|algebraic topology]], several other algebras of this type occur, among these the lambda algebra and the Dyer–Lashof algebra of homology operations and are related to the Dickson algebra ([[#References|[a6]]], [[#References|[a9]]], [[#References|[a10]]]). | ||
| + | |||
| + | The corresponding algebras of invariants have been computed when $\operatorname{GL} ( V )$ is replaced by a special linear group, an orthogonal group, a unitary group or a symplectic group ([[#References|[a2]]], p. 92, [[#References|[a3]]]). | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J.F. Adams, C.W. Wilkerson, "Finite H-spaces and algebras over the Steenrod algebra" ''Ann. Math.'' , '''111''' (1980) pp. 95–143</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> D. Benson, "Polynomial invariants of finite groups" , ''London Math. Soc. Lecture Notes'' , '''190''' , Cambridge Univ. Press (1993)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> D. Carlisle, P. Kropholler, "Rational invariants of certain orthogonal and unitary groups" ''Bull. London Math. Soc.'' , '''24''' : 1 (1992) pp. 57–60</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> H.A.E. Campbell, I. Highes, R.D. Pollack, "Rings of invariants and $p$-Sylow subgroups" ''Canad. Bull. Math.'' , '''34''' (1991) pp. 42–47</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> L.E. Dickson, "A fundamental system of invariants of the general modular linear group with a solution of the form problem" ''Trans. Amer. Math. Soc.'' , '''12''' (1911) pp. 75–98</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> I. Madsen, "On the action of the Dyer–Lashof algebra on $H ^ { * } ( G )$" ''Pacific J. Math.'' , '''60''' (1975) pp. 235–275</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> D.G. Quillen, "The mod two cohomology rings of extra-special $2$-groups and the Spinor groups" ''Math. Ann.'' , '''194''' (1971) pp. 197–212</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> L. Smith, R. Switzer, "Realizability and nonrealizability of Dickson algebras as cohomology rings" ''Proc. Amer. Math. Soc.'' , '''89''' (1983) pp. 303–313</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> W.M. Singer, "Invariant theory and the lambda algebra" ''Trans. Amer. Math. Soc.'' , '''280''' (1983) pp. 673–693</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> C.W. Wilkerson, "A primer on the Dickson invariants" ''Contemp. Math.'' , '''19''' (1983) pp. 421–434</td></tr></table> |
Revision as of 16:57, 1 July 2020
Let $\mathbf{F} _ { q }$ denote the field with $q$ elements (cf. Finite field) and $V$ an $n$-dimensional $\mathbf{F} _ { q }$-vector space (cf. also Vector space). Let $S ( V )$ denote the symmetric algebra generated by $V$ over $\mathbf{F} _ { q }$. Since the general linear group, $\operatorname{GL} ( V ) = \operatorname { Aut } _ { \mathbf{F} _ { q } } ( V )$, acts on $V$, there is an induced action on the algebra $S ( V )$. L.E. Dickson determined the structure of the $\operatorname{GL} ( V )$-fixed subalgebra, $S ( V ) ^ { G L ( V ) }$, now known as the Dickson algebra. In [a5] (see also [a2], p. 90) $S ( V ) ^ { \operatorname{GL} ( V ) }$ was shown to be a polynomial algebra of the form 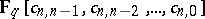 where the $\{ c _ { n,j } \}$ are homogeneous polynomials in $S ( V )$, called the Dickson invariants (sometimes this term is used to refer to any element of the Dickson algebra), and are constructed in the following manner. Let $K$ be a field extension of $\mathbf{F} _ { q }$ which contains $V$ (cf. also Extension of a field). Then the monic separable polynomial whose roots are precisely the elements of $V$ has the form
where the $\{ c _ { n,j } \}$ are homogeneous polynomials in $S ( V )$, called the Dickson invariants (sometimes this term is used to refer to any element of the Dickson algebra), and are constructed in the following manner. Let $K$ be a field extension of $\mathbf{F} _ { q }$ which contains $V$ (cf. also Extension of a field). Then the monic separable polynomial whose roots are precisely the elements of $V$ has the form
\begin{equation*} f ( X ) = X ^ { q ^ { n } } + \sum _ { i = 0 } ^ { n - 1 } ( - 1 ) ^ { n - i } c _ { n , i } X ^ { q ^ { i } } \in K [ X ]. \end{equation*}
Suppose that $W$ is an $n$-dimensional $\mathbf{F} _ { p }$-vector space ($p$ a prime number). When $p = 2$, the cohomology algebra $H ^ { * } ( W ; \mathbf{F} _ { 2 } )$ is isomorphic to $S ( H ^ { 1 } ( W ; \mathbf{F} _ { 2 } ) )$. Therefore, over $\mathbf{F} _ { p }$ it is natural to endow $S ( V )$ with the structure of a graded algebra with $V$ of dimension one if $p = 2$ and of dimension two if $p$ is odd.
In this topological manifestation, the Dickson algebra has proved very useful ([a1], [a4], [a8], [a10]). For example, if $\rho : W \rightarrow O _ { 2^{n} } ( \mathbf{R} )$ is the real regular representation of $W$ and $V = H ^ { 1 } ( W ; \mathbf{F} _ { 2 } )$, then the Stiefel–Whitney class satisfies $w _ { 2 ^ { n } - 2 ^ { i } } ( \rho ) = c _ { n , i }$ [a7]. When $p$ is odd, $c _ { n , i }$ is related in a similar manner to Chern classes of the regular representation. The observation shows that the Dickson algebra becomes a graded algebra together with an action by the Steenrod algebra of cohomology operations. In algebraic topology, several other algebras of this type occur, among these the lambda algebra and the Dyer–Lashof algebra of homology operations and are related to the Dickson algebra ([a6], [a9], [a10]).
The corresponding algebras of invariants have been computed when $\operatorname{GL} ( V )$ is replaced by a special linear group, an orthogonal group, a unitary group or a symplectic group ([a2], p. 92, [a3]).
References
| [a1] | J.F. Adams, C.W. Wilkerson, "Finite H-spaces and algebras over the Steenrod algebra" Ann. Math. , 111 (1980) pp. 95–143 |
| [a2] | D. Benson, "Polynomial invariants of finite groups" , London Math. Soc. Lecture Notes , 190 , Cambridge Univ. Press (1993) |
| [a3] | D. Carlisle, P. Kropholler, "Rational invariants of certain orthogonal and unitary groups" Bull. London Math. Soc. , 24 : 1 (1992) pp. 57–60 |
| [a4] | H.A.E. Campbell, I. Highes, R.D. Pollack, "Rings of invariants and $p$-Sylow subgroups" Canad. Bull. Math. , 34 (1991) pp. 42–47 |
| [a5] | L.E. Dickson, "A fundamental system of invariants of the general modular linear group with a solution of the form problem" Trans. Amer. Math. Soc. , 12 (1911) pp. 75–98 |
| [a6] | I. Madsen, "On the action of the Dyer–Lashof algebra on $H ^ { * } ( G )$" Pacific J. Math. , 60 (1975) pp. 235–275 |
| [a7] | D.G. Quillen, "The mod two cohomology rings of extra-special $2$-groups and the Spinor groups" Math. Ann. , 194 (1971) pp. 197–212 |
| [a8] | L. Smith, R. Switzer, "Realizability and nonrealizability of Dickson algebras as cohomology rings" Proc. Amer. Math. Soc. , 89 (1983) pp. 303–313 |
| [a9] | W.M. Singer, "Invariant theory and the lambda algebra" Trans. Amer. Math. Soc. , 280 (1983) pp. 673–693 |
| [a10] | C.W. Wilkerson, "A primer on the Dickson invariants" Contemp. Math. , 19 (1983) pp. 421–434 |
Dickson algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dickson_algebra&oldid=15987