Difference between revisions of "Sylow basis"
From Encyclopedia of Mathematics
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915401.png" /> be a [[Finite group|finite group]] and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915402.png" /> a subset of the prime numbers that divide the order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915403.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915404.png" />. A Sylow <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915406.png" />-basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915407.png" /> is a collection of Sylow <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915408.png" />-subgroups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915409.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154010.png" /> (cf. [[Sylow subgroup|Sylow subgroup]]), one for each prime <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154011.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154012.png" />, such that: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154013.png" /> are in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154014.png" />, then the order of every element in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154015.png" /> (the subgroup generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154016.png" />) is a product of non-negative powers of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154017.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154018.png" /> is the set of all primes dividing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154019.png" />, one speaks of a complete Sylow basis. Two Sylow bases are conjugate if there is a single element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154020.png" /> that by conjugation transforms all the groups of the first into those of the second. Hall's second theorem, [[#References|[a2]]], says that every finite solvable group has a complete Sylow basis, and that all these bases are conjugate. Conversely, if a finite group has a complete Sylow basis, then it is solvable (cf. also [[Solvable group|Solvable group]]). | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915401.png" /> be a [[Finite group|finite group]] and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915402.png" /> a subset of the prime numbers that divide the order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915403.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915404.png" />. A Sylow <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915406.png" />-basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915407.png" /> is a collection of Sylow <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915408.png" />-subgroups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s0915409.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154010.png" /> (cf. [[Sylow subgroup|Sylow subgroup]]), one for each prime <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154011.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154012.png" />, such that: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154013.png" /> are in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154014.png" />, then the order of every element in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154015.png" /> (the subgroup generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154016.png" />) is a product of non-negative powers of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154017.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154018.png" /> is the set of all primes dividing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154019.png" />, one speaks of a complete Sylow basis. Two Sylow bases are conjugate if there is a single element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091540/s09154020.png" /> that by [[conjugation]] transforms all the groups of the first into those of the second. Hall's second theorem, [[#References|[a2]]], says that every finite solvable group has a complete Sylow basis, and that all these bases are conjugate. Conversely, if a finite group has a complete Sylow basis, then it is solvable (cf. also [[Solvable group|Solvable group]]). |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.G. Kurosh, "The theory of groups" , '''2''' , Chelsea (1960) pp. 195ff (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Hall, "On the Sylow systems of a soluble group" ''Proc. London Math. Soc.'' , '''43''' (1937) pp. 316–323</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.G. Kurosh, "The theory of groups" , '''2''' , Chelsea (1960) pp. 195ff (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Hall, "On the Sylow systems of a soluble group" ''Proc. London Math. Soc.'' , '''43''' (1937) pp. 316–323</TD></TR></table> | ||
Revision as of 21:18, 29 November 2014
Let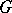 
be a finite group and 
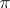a subset of the prime numbers that divide the order 
of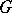 
. A Sylow 
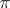-basis 
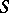is a collection of Sylow 
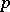-subgroups 
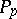of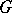 
(cf. Sylow subgroup), one for each prime 
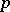in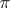 
, such that: If 
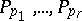are in 
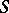, then the order of every element in 
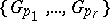(the subgroup generated by 
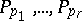) is a product of non-negative powers of 
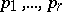. If 
is the set of all primes dividing 
, one speaks of a complete Sylow basis. Two Sylow bases are conjugate if there is a single element of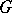 
that by conjugation transforms all the groups of the first into those of the second. Hall's second theorem, [a2], says that every finite solvable group has a complete Sylow basis, and that all these bases are conjugate. Conversely, if a finite group has a complete Sylow basis, then it is solvable (cf. also Solvable group).
References
| [a1] | A.G. Kurosh, "The theory of groups" , 2 , Chelsea (1960) pp. 195ff (Translated from Russian) |
| [a2] | P. Hall, "On the Sylow systems of a soluble group" Proc. London Math. Soc. , 43 (1937) pp. 316–323 |
How to Cite This Entry:
Sylow basis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sylow_basis&oldid=15735
Sylow basis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sylow_basis&oldid=15735