Difference between revisions of "Sinusoid"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX encoding is done + graph) |
||
| Line 1: | Line 1: | ||
| − | + | {{TEX|done}} | |
| − | + | The graph of the function $y=\sin x$ (see Fig.). The sinusoid is a continuous curve with period $T=2\pi$. It intersects the $x$-axis at the points $(k\pi, 0)$. These are also points of inflection, meeting the $x$-axis at an angle of $\pm\pi/4$. The extrema are at the points $((k+1/2)\pi, (-1)^k)$. | |
| − | + | <asy> | |
| + | import graph; | ||
| + | size(500,200,IgnoreAspect); | ||
| + | real f(real x) {return sin(x);}; | ||
| − | + | real f1(real x) {return cos(x);}; | |
| + | draw(graph(f1,-2*pi,2*pi),blue,"$\cos(x)$"); | ||
| + | draw(graph(f,-2*pi,2*pi),red,"$\sin(x)$"); | ||
| + | xaxis("$x$",Arrow); | ||
| + | yaxis(); | ||
| − | + | xtick("$\frac{\pi}{6}$",pi/6,N); | |
| + | xtick("$\frac{\pi}{4}$",pi/4,N); | ||
| + | xtick("$\frac{\pi}{3}$",pi/3,N); | ||
| + | xtick("$\frac{\pi}{2}$",pi/2,N); | ||
| + | xtick("$\frac{3\pi}{2}$",3*pi/2,N); | ||
| + | xtick("$\pi$",pi,N); | ||
| + | xtick("$2\pi$",2*pi,N); | ||
| + | xtick("$-\frac{\pi}{2}$",-pi/2,N); | ||
| + | xtick("$-\frac{3\pi}{2}$",-3*pi/2,N); | ||
| + | xtick("$-\pi$",-pi,N); | ||
| + | xtick("$-2\pi$",-2*pi,N); | ||
| + | ytick("$1/2$",0.5,1); | ||
| + | ytick("$\sqrt{2}/2$",sqrt(2)/2,1); | ||
| + | ytick("$\sqrt{3}/2$",sqrt(3)/2,1); | ||
| + | ytick("$1$",1,1); | ||
| + | ytick("$-1/2$",-0.5,-1); | ||
| + | ytick("$-\sqrt{2}/2$",-sqrt(2)/2,-1); | ||
| + | ytick("$-\sqrt{3}/2$",-sqrt(3)/2,-1); | ||
| + | ytick("$-1$",-1,-1); | ||
| + | attach(legend(),truepoint(E),10E,UnFill); | ||
| + | </asy> | ||
| − | ==== | + | The graph of $y=\cos x = \sin(x+\pi/2)$ is the cosinusoid, obtained by shifting the sinusoid a distance of $\pi/2$ to the left. The cosinusoid intersects the $x$-axis at the points $((k+1/2)\pi,0)$, and its extrema are at the points $(k\pi, (-1)^k)$. |
| − | + | ||
| + | Many oscillatory processes can be described by a periodic function of the form y=a\sin(bx+c), where $a$, $b$ and $c$ are constants and $b>0$. The graph of this function (called a general sinusoid) is obtained from the graph of $y=\sin x$ (the ordinary sinusoid) as follows: expand in the direction of the $y$-axis by a factor $|a|$, contract in the $x$-direction by a factor $b$, translate to the left over a distance $c/b$, and when $a<0$: reflect in the $x$-axis. Its period is $T=2\pi/b$ and it meets the $x$-axis at the points $((k\pi-c)/b,0)$. Its extrema are at the points $(((k+1/2)\pi-c)/b,(-1)^ka)$. | ||
| + | |||
| + | In this article, $k\in \mathbb Z$. | ||
See also [[Sine|Sine]]; [[Trigonometric functions|Trigonometric functions]]. | See also [[Sine|Sine]]; [[Trigonometric functions|Trigonometric functions]]. | ||
Revision as of 18:49, 5 December 2012
The graph of the function $y=\sin x$ (see Fig.). The sinusoid is a continuous curve with period $T=2\pi$. It intersects the $x$-axis at the points $(k\pi, 0)$. These are also points of inflection, meeting the $x$-axis at an angle of $\pm\pi/4$. The extrema are at the points $((k+1/2)\pi, (-1)^k)$.
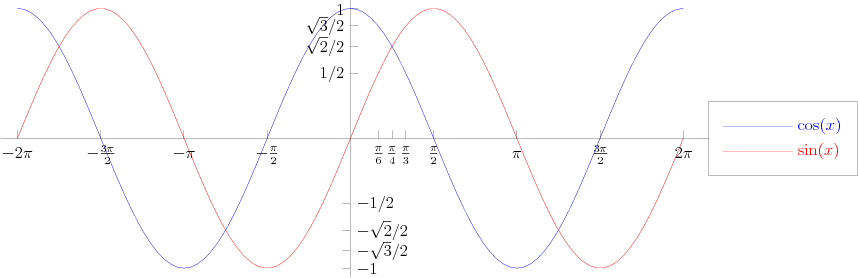
The graph of $y=\cos x = \sin(x+\pi/2)$ is the cosinusoid, obtained by shifting the sinusoid a distance of $\pi/2$ to the left. The cosinusoid intersects the $x$-axis at the points $((k+1/2)\pi,0)$, and its extrema are at the points $(k\pi, (-1)^k)$.
Many oscillatory processes can be described by a periodic function of the form y=a\sin(bx+c), where $a$, $b$ and $c$ are constants and $b>0$. The graph of this function (called a general sinusoid) is obtained from the graph of $y=\sin x$ (the ordinary sinusoid) as follows: expand in the direction of the $y$-axis by a factor $|a|$, contract in the $x$-direction by a factor $b$, translate to the left over a distance $c/b$, and when $a<0$: reflect in the $x$-axis. Its period is $T=2\pi/b$ and it meets the $x$-axis at the points $((k\pi-c)/b,0)$. Its extrema are at the points $(((k+1/2)\pi-c)/b,(-1)^ka)$.
In this article, $k\in \mathbb Z$.
See also Sine; Trigonometric functions.
How to Cite This Entry:
Sinusoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sinusoid&oldid=15670
Sinusoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sinusoid&oldid=15670
This article was adapted from an original article by Yu.A. Gor'kov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article