Difference between revisions of "Random field, generalized"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | r0773101.png | ||
| + | $#A+1 = 48 n = 1 | ||
| + | $#C+1 = 48 : ~/encyclopedia/old_files/data/R077/R.0707310 Random field, generalized, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''generalized stochastic process'' | ''generalized stochastic process'' | ||
| − | A [[Random function|random function]] on a smooth manifold | + | A [[Random function|random function]] on a smooth manifold $ G $, |
| + | the typical realizations of which are generalized functions defined on $ G $. | ||
| + | More precisely, let $ G $ | ||
| + | be a $ C ^ \infty $ | ||
| + | manifold (a smooth manifold) and let $ D ( G) $ | ||
| + | be the space of infinitely-differentiable functions of compact support defined on $ G $, | ||
| + | with the usual topology of uniform convergence of sequence of functions of uniformly compact support and all their derivatives. Then a generalized random field can be defined on $ G $ | ||
| + | in terms of a given continuous linear mapping | ||
| − | + | $$ | |
| + | D ( G) \rightarrow L _ {0} ( \omega , \mathfrak B , \mu ) ,\ \ | ||
| + | \phi \rightarrow f _ \phi ,\ \phi \in D ( G) , | ||
| + | $$ | ||
| − | from | + | from $ D ( G) $ |
| + | into the space $ L _ {0} ( \omega , \mathfrak B , \mu ) $ | ||
| + | of random variables defined on some probability space $ \Omega $ | ||
| + | with a specified $ \sigma $- | ||
| + | algebra $ \mathfrak B $ | ||
| + | of subsets and a probability measure $ \mu $ | ||
| + | defined on $ \mathfrak B $; | ||
| + | $ L _ {0} ( \Omega , \mathfrak B , \mu ) $ | ||
| + | is equipped with the topology of [[Convergence in measure|convergence in measure]] [[#References|[7]]]. In the case when the probability space is the space $ D ^ \prime ( G) $ | ||
| + | of generalized functions on $ G $ | ||
| + | with $ \sigma $- | ||
| + | algebra $ \mathfrak B _ {0} $ | ||
| + | generated by the cylindrical sets in $ D ^ \prime ( G) $, | ||
| + | (cf. [[Generalized functions, space of|Generalized functions, space of]]; [[Cylinder set|Cylinder set]]) and the mapping is given by | ||
| − | + | $$ | |
| + | f _ \phi ( T) = ( T , \phi ) ,\ \ | ||
| + | T \in D ^ \prime ( G) ,\ \phi \in D ( G) , | ||
| + | $$ | ||
| − | the generalized random field | + | the generalized random field $ \{ {f _ \phi } : {\phi \in D ^ \prime ( G) } \} $ |
| + | is called canonical. It turns out that any generalized random field on a finite-dimensional manifold $ G $ | ||
| + | is probabilistically isomorphic to a certain (unique) canonical random field on $ G $( | ||
| + | see [[#References|[2]]]). | ||
| − | This definition admits a number of natural modifications; for example, one can consider vector-valued generalized random fields or, instead of the space | + | This definition admits a number of natural modifications; for example, one can consider vector-valued generalized random fields or, instead of the space $ D ( G) $, |
| + | use some more extensive space of test functions on $ G $ | ||
| + | in the definition (such as, in the case $ G = \mathbf R ^ {n} $, | ||
| + | $ n = 1 , 2 \dots $ | ||
| + | the space $ S ( \mathbf R ^ {n} ) $ | ||
| + | of $ C ^ \infty $ | ||
| + | differentiable functions which, together with all derivatives, decrease faster than any negative power $ | x | ^ {k} $, | ||
| + | $ k = - 1 , - 2 \dots $ | ||
| + | $ x \in \mathbf R ^ {n} $). | ||
| − | The concept of a generalized random field includes the classical random fields and processes whose realizations are ordinary functions. This concept arose in the mid-1950s, when it became apparent that many natural stochastic constructs cannot be sufficiently simply expressed in terms of classical random fields, but have in the language of generalized random fields a simple and elegant description. For example, any positive-definite bilinear form on | + | The concept of a generalized random field includes the classical random fields and processes whose realizations are ordinary functions. This concept arose in the mid-1950s, when it became apparent that many natural stochastic constructs cannot be sufficiently simply expressed in terms of classical random fields, but have in the language of generalized random fields a simple and elegant description. For example, any positive-definite bilinear form on $ D ( \mathbf R ^ {n} ) $, |
| + | $ n = 1 , 2 \dots $ | ||
| − | + | $$ | |
| + | ( \phi _ {1} , \phi _ {2} ) = \ | ||
| + | \int\limits _ {\mathbf R ^ {n} } | ||
| + | \int\limits _ {\mathbf R ^ {n} } W ( x _ {1} , x _ {2} ) \phi | ||
| + | ( x _ {1} ) \phi ( x _ {2} ) d x _ {1} d x _ {2} , | ||
| + | $$ | ||
| − | + | $ \phi _ {1} , \phi _ {2} \in D ( \mathbf R ^ {n} ) $, | |
| + | where $ W ( x _ {1} , x _ {2} ) $ | ||
| + | is a positive-definite symmetric generalized function of two variables, determines a unique Gaussian generalized random field $ \{ {f _ \phi } : {\phi \in D ( \mathbf R ^ {n} ) } \} $ | ||
| + | on $ \mathbf R ^ {n} $( | ||
| + | with zero average) such that the covariance of this field is | ||
| − | + | $$ | |
| + | \int\limits f _ {\phi _ {1} } f _ {\phi _ {2} } \ | ||
| + | d \mu = ( \phi _ {1} , \phi _ {2} ) , | ||
| + | $$ | ||
| − | where | + | where $ \mu $ |
| + | is the probability measure on $ D ^ \prime ( \mathbf R ^ {n} ) $ | ||
| + | corresponding to this field. This generalized random field turns out to be classical only if the function $ W ( x _ {1} , x _ {2} ) $ | ||
| + | is sufficiently good (for example, continuous and bounded). Other examples are: generalized random fields on $ \mathbf R ^ {n} $( | ||
| + | see [[#References|[6]]]), among which there are no classical fields. | ||
| − | Interest in the study of generalized random fields (and especially of Markov fields) has grown recently due to the connection, discovered in the early 1970s, between the problem of constructing physical quantum fields and Markov generalized random fields on | + | Interest in the study of generalized random fields (and especially of Markov fields) has grown recently due to the connection, discovered in the early 1970s, between the problem of constructing physical quantum fields and Markov generalized random fields on $ \mathbf R ^ {n} $ |
| + | when $ n > 1 $( | ||
| + | see [[#References|[5]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.M. Gel'fand, G.E. Shilov, "Generalized functions. Spaces of fundamental and generalized functions" , Acad. Press (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , '''4''' , Acad. Press (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.M. Gel'fand, "Generalized random processes" ''Dokl. Akad. Nauk SSSR'' , '''100''' : 5 (1955) pp. 853–856 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Itô, "Stationary random distributions" ''Mem. Coll. Sci. Univ. Kyoto Ser. A.'' , '''28''' : 3 (1954) pp. 209–223</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Simon, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077310/r07731049.png" /> Euclidean (quantum) field theory" , Princeton Univ. Press (1974)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> R.L. Dobrushin, "Automodel generalized random fields and their renorm group" R.L. Dobrushin (ed.) Ya.G. Sinai (ed.) , ''Multicomponent Random Sets'' , M. Dekker (1980) pp. 153–198 (Translated from Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R.L. Dobrushin, R.A. Minlos, "Polynomials in linear random functions" ''Russian Math. Surveys'' , '''32''' : 2 (1971) pp. 71–127 ''Uspekhi Mat. Nauk'' , '''32''' : 2 (1977) pp. 67–122</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.M. Gel'fand, G.E. Shilov, "Generalized functions. Spaces of fundamental and generalized functions" , Acad. Press (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , '''4''' , Acad. Press (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.M. Gel'fand, "Generalized random processes" ''Dokl. Akad. Nauk SSSR'' , '''100''' : 5 (1955) pp. 853–856 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Itô, "Stationary random distributions" ''Mem. Coll. Sci. Univ. Kyoto Ser. A.'' , '''28''' : 3 (1954) pp. 209–223</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Simon, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077310/r07731049.png" /> Euclidean (quantum) field theory" , Princeton Univ. Press (1974)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> R.L. Dobrushin, "Automodel generalized random fields and their renorm group" R.L. Dobrushin (ed.) Ya.G. Sinai (ed.) , ''Multicomponent Random Sets'' , M. Dekker (1980) pp. 153–198 (Translated from Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R.L. Dobrushin, R.A. Minlos, "Polynomials in linear random functions" ''Russian Math. Surveys'' , '''32''' : 2 (1971) pp. 71–127 ''Uspekhi Mat. Nauk'' , '''32''' : 2 (1977) pp. 67–122</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Latest revision as of 08:09, 6 June 2020
generalized stochastic process
A random function on a smooth manifold $ G $, the typical realizations of which are generalized functions defined on $ G $. More precisely, let $ G $ be a $ C ^ \infty $ manifold (a smooth manifold) and let $ D ( G) $ be the space of infinitely-differentiable functions of compact support defined on $ G $, with the usual topology of uniform convergence of sequence of functions of uniformly compact support and all their derivatives. Then a generalized random field can be defined on $ G $ in terms of a given continuous linear mapping
$$ D ( G) \rightarrow L _ {0} ( \omega , \mathfrak B , \mu ) ,\ \ \phi \rightarrow f _ \phi ,\ \phi \in D ( G) , $$
from $ D ( G) $ into the space $ L _ {0} ( \omega , \mathfrak B , \mu ) $ of random variables defined on some probability space $ \Omega $ with a specified $ \sigma $- algebra $ \mathfrak B $ of subsets and a probability measure $ \mu $ defined on $ \mathfrak B $; $ L _ {0} ( \Omega , \mathfrak B , \mu ) $ is equipped with the topology of convergence in measure [7]. In the case when the probability space is the space $ D ^ \prime ( G) $ of generalized functions on $ G $ with $ \sigma $- algebra $ \mathfrak B _ {0} $ generated by the cylindrical sets in $ D ^ \prime ( G) $, (cf. Generalized functions, space of; Cylinder set) and the mapping is given by
$$ f _ \phi ( T) = ( T , \phi ) ,\ \ T \in D ^ \prime ( G) ,\ \phi \in D ( G) , $$
the generalized random field $ \{ {f _ \phi } : {\phi \in D ^ \prime ( G) } \} $ is called canonical. It turns out that any generalized random field on a finite-dimensional manifold $ G $ is probabilistically isomorphic to a certain (unique) canonical random field on $ G $( see [2]).
This definition admits a number of natural modifications; for example, one can consider vector-valued generalized random fields or, instead of the space $ D ( G) $, use some more extensive space of test functions on $ G $ in the definition (such as, in the case $ G = \mathbf R ^ {n} $, $ n = 1 , 2 \dots $ the space $ S ( \mathbf R ^ {n} ) $ of $ C ^ \infty $ differentiable functions which, together with all derivatives, decrease faster than any negative power $ | x | ^ {k} $, $ k = - 1 , - 2 \dots $ $ x \in \mathbf R ^ {n} $).
The concept of a generalized random field includes the classical random fields and processes whose realizations are ordinary functions. This concept arose in the mid-1950s, when it became apparent that many natural stochastic constructs cannot be sufficiently simply expressed in terms of classical random fields, but have in the language of generalized random fields a simple and elegant description. For example, any positive-definite bilinear form on $ D ( \mathbf R ^ {n} ) $, $ n = 1 , 2 \dots $
$$ ( \phi _ {1} , \phi _ {2} ) = \ \int\limits _ {\mathbf R ^ {n} } \int\limits _ {\mathbf R ^ {n} } W ( x _ {1} , x _ {2} ) \phi ( x _ {1} ) \phi ( x _ {2} ) d x _ {1} d x _ {2} , $$
$ \phi _ {1} , \phi _ {2} \in D ( \mathbf R ^ {n} ) $, where $ W ( x _ {1} , x _ {2} ) $ is a positive-definite symmetric generalized function of two variables, determines a unique Gaussian generalized random field $ \{ {f _ \phi } : {\phi \in D ( \mathbf R ^ {n} ) } \} $ on $ \mathbf R ^ {n} $( with zero average) such that the covariance of this field is
$$ \int\limits f _ {\phi _ {1} } f _ {\phi _ {2} } \ d \mu = ( \phi _ {1} , \phi _ {2} ) , $$
where $ \mu $ is the probability measure on $ D ^ \prime ( \mathbf R ^ {n} ) $ corresponding to this field. This generalized random field turns out to be classical only if the function $ W ( x _ {1} , x _ {2} ) $ is sufficiently good (for example, continuous and bounded). Other examples are: generalized random fields on $ \mathbf R ^ {n} $( see [6]), among which there are no classical fields.
Interest in the study of generalized random fields (and especially of Markov fields) has grown recently due to the connection, discovered in the early 1970s, between the problem of constructing physical quantum fields and Markov generalized random fields on $ \mathbf R ^ {n} $ when $ n > 1 $( see [5]).
References
| [1] | I.M. Gel'fand, G.E. Shilov, "Generalized functions. Spaces of fundamental and generalized functions" , Acad. Press (1968) (Translated from Russian) |
| [2] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1968) (Translated from Russian) |
| [3] | I.M. Gel'fand, "Generalized random processes" Dokl. Akad. Nauk SSSR , 100 : 5 (1955) pp. 853–856 (In Russian) |
| [4] | H. Itô, "Stationary random distributions" Mem. Coll. Sci. Univ. Kyoto Ser. A. , 28 : 3 (1954) pp. 209–223 |
| [5] | B. Simon, "The 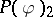 Euclidean (quantum) field theory" , Princeton Univ. Press (1974) Euclidean (quantum) field theory" , Princeton Univ. Press (1974) |
| [6] | R.L. Dobrushin, "Automodel generalized random fields and their renorm group" R.L. Dobrushin (ed.) Ya.G. Sinai (ed.) , Multicomponent Random Sets , M. Dekker (1980) pp. 153–198 (Translated from Russian) |
| [7] | R.L. Dobrushin, R.A. Minlos, "Polynomials in linear random functions" Russian Math. Surveys , 32 : 2 (1971) pp. 71–127 Uspekhi Mat. Nauk , 32 : 2 (1977) pp. 67–122 |
Comments
Cf. also Random field.
References
| [a1] | A.M. Yaglom, "Correlation theory of stationary and related random functions" , 1–2 , Springer (1987) (Translated from Russian) |
| [a2] | S. Albeverio, R. Høegh-Krohn, B. Zegarlinski, "Uniqueness and global Markov property for Euclidean fields: the case of general polynomial interactions" Commun. Math. Phys. , 123 (1989) pp. 377–424 |
| [a3] | Yu.A. Rozanov, "Markov random fields" , Springer (1982) (Translated from Russian) |
Random field, generalized. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Random_field,_generalized&oldid=15473