Difference between revisions of "Hodograph"
(Importing text file) |
(TeX done) |
||
| Line 1: | Line 1: | ||
| − | + | {{TEX|done}} | |
| − | The curve representing the ends of the variable vector | + | ''of a vector field $x(t)$ along a curve'' |
| + | |||
| + | The curve representing the ends of the variable vector $x(t)$ ($t$ is a real variable, such as time) whose origin for all $t$ is a given fixed point $O$. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/h047500a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/h047500a.gif" /> | ||
| Line 7: | Line 9: | ||
Figure: h047500a | Figure: h047500a | ||
| − | The hodograph is a visual geometrical representation of the variation (with | + | The hodograph is a visual geometrical representation of the variation (with $t$) of the magnitude represented by the variable vector and of the rate of this change. Its direction is that of the tangent to the hodograph. For example, if the velocity of a moving point is represented by a variable vector $\mathbf{v}$, then by drawing the values of $\mathbf{v}$ at different moments of time from the origin $O$, one obtains the velocity hodograph. The magnitude describing the rate of the variation of the velocity at some point $M$, i.e. the acceleration $\mathbf{w}$ at that point, has at any point of time the direction of the tangent to the velocity hodograph at the respective point. |
Latest revision as of 19:16, 12 April 2017
of a vector field $x(t)$ along a curve
The curve representing the ends of the variable vector $x(t)$ ($t$ is a real variable, such as time) whose origin for all $t$ is a given fixed point $O$.
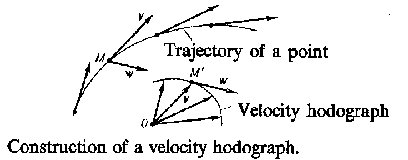
Figure: h047500a
The hodograph is a visual geometrical representation of the variation (with $t$) of the magnitude represented by the variable vector and of the rate of this change. Its direction is that of the tangent to the hodograph. For example, if the velocity of a moving point is represented by a variable vector $\mathbf{v}$, then by drawing the values of $\mathbf{v}$ at different moments of time from the origin $O$, one obtains the velocity hodograph. The magnitude describing the rate of the variation of the velocity at some point $M$, i.e. the acceleration $\mathbf{w}$ at that point, has at any point of time the direction of the tangent to the velocity hodograph at the respective point.
Hodograph. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hodograph&oldid=15147