|
|
| Line 1: |
Line 1: |
| − | The general name for theorems that give upper bounds for the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d0311601.png" /> of zeros <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d0311602.png" /> of Dirichlet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d0311604.png" />-functions | + | {{TEX|done}} |
| | + | The general name for theorems that give upper bounds for the number $N(\sigma,T,\chi)$ of zeros $\rho=\beta+i\gamma$ of Dirichlet $L$-functions |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d0311605.png" /></td> </tr></table>
| + | $$L(s,\chi)=\sum_{n=1}^\infty\frac{\chi(n,k)}{n^s},$$ |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d0311606.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d0311607.png" /> is a character modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d0311608.png" />, in the rectangle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d0311609.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116010.png" />. In the case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116011.png" />, one gets density theorems for the number of zeros of the Riemann zeta-function | + | where $s=\sigma+it$ and $\chi(n,k)$ is a character modulo $k$, in the rectangle $1/2<\sigma\leq\beta<1$, $|\gamma|\leq T$. In the case $k=1$, one gets density theorems for the number of zeros of the Riemann zeta-function |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116012.png" /></td> </tr></table>
| + | $$\zeta(s)=\sum_{n=1}^\infty\frac{1}{n^s}.$$ |
| | | | |
| − | The density theorems for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116013.png" />-functions with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116014.png" /> are more complicated than those for the Riemann zeta-function. As <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116016.png" /> increase, one obtains bounds depending on these parameters. The parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116017.png" /> plays a decisive part in applications. | + | The density theorems for $L$-functions with $k\neq1$ are more complicated than those for the Riemann zeta-function. As $T$ and $k$ increase, one obtains bounds depending on these parameters. The parameter $k$ plays a decisive part in applications. |
| | | | |
| − | The significance of density theorems is evident from the relations enabling one to estimate the residual term in the formula for the number of prime numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116018.png" /> belonging to an arithmetic progression <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116019.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116020.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116021.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116022.png" /> and not exceeding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116023.png" />, as a function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116024.png" />. | + | The significance of density theorems is evident from the relations enabling one to estimate the residual term in the formula for the number of prime numbers $p$ belonging to an arithmetic progression $km+l$, $1\leq l\leq k$, $(l,k)=1$, $m=0,1,\ldots,$ and not exceeding $x$, as a function of $N(\sigma,T,\chi)$. |
| | | | |
| − | Since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116025.png" /> does not increase with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116026.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116027.png" />, the purpose of density theorems is to obtain bounds that converge most rapidly to zero as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116028.png" />. In turn, these bounds are substantially supplemented by results on the absence of zeros for Dirichlet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116029.png" />-functions in neighbourhoods of the straight line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116030.png" />, obtained using the Hardy–Littlewood–Vinogradov circle method. In this way it has been possible to obtain strong bounds for the amount of even numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116031.png" /> that cannot be represented as the sum of two prime numbers. | + | Since $N(\sigma,T,\chi)$ does not increase with $\sigma$ and $N(1,T,\chi)=0$, the purpose of density theorems is to obtain bounds that converge most rapidly to zero as $\sigma\to1$. In turn, these bounds are substantially supplemented by results on the absence of zeros for Dirichlet $L$-functions in neighbourhoods of the straight line $\sigma=1$, obtained using the Hardy–Littlewood–Vinogradov circle method. In this way it has been possible to obtain strong bounds for the amount of even numbers $n\leq x$ that cannot be represented as the sum of two prime numbers. |
| | | | |
| − | Yu.V. Linnik obtained the first density theorems providing bounds for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116032.png" /> for an individual character <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116033.png" /> and averaged bounds over all characters modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116034.png" />, given <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116035.png" />. Subsequent substantial improvements of density theorems were obtained by A.I. Vinogradov and E. Bombieri, who used bounds on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116036.png" /> averaged over all moduli <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116037.png" /> and over all primitive characters modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116038.png" />, given <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116039.png" />, in proving a theorem on the average distribution of prime numbers in arithmetic progressions (for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d031/d031160/d03116040.png" />). The Vinogradov–Bombieri theorem enables one to replace the generalized Riemann hypothesis in various classical problems in additive number theory. There are also various other improvements of density theorems. | + | Yu.V. Linnik obtained the first density theorems providing bounds for $N(\sigma,T,\chi)$ for an individual character $\chi$ and averaged bounds over all characters modulo $a$, given $k$. Subsequent substantial improvements of density theorems were obtained by A.I. Vinogradov and E. Bombieri, who used bounds on $N(\sigma,T,\chi)$ averaged over all moduli $k\leq Q$ and over all primitive characters modulo $a$, given $k$, in proving a theorem on the average distribution of prime numbers in arithmetic progressions (for $Q=\sqrt x/(\ln x)^c$). The Vinogradov–Bombieri theorem enables one to replace the generalized Riemann hypothesis in various classical problems in additive number theory. There are also various other improvements of density theorems. |
| | | | |
| | ====References==== | | ====References==== |
Revision as of 20:16, 31 July 2014
The general name for theorems that give upper bounds for the number $N(\sigma,T,\chi)$ of zeros $\rho=\beta+i\gamma$ of Dirichlet $L$-functions
$$L(s,\chi)=\sum_{n=1}^\infty\frac{\chi(n,k)}{n^s},$$
where $s=\sigma+it$ and $\chi(n,k)$ is a character modulo $k$, in the rectangle $1/2<\sigma\leq\beta<1$, $|\gamma|\leq T$. In the case $k=1$, one gets density theorems for the number of zeros of the Riemann zeta-function
$$\zeta(s)=\sum_{n=1}^\infty\frac{1}{n^s}.$$
The density theorems for $L$-functions with $k\neq1$ are more complicated than those for the Riemann zeta-function. As $T$ and $k$ increase, one obtains bounds depending on these parameters. The parameter $k$ plays a decisive part in applications.
The significance of density theorems is evident from the relations enabling one to estimate the residual term in the formula for the number of prime numbers $p$ belonging to an arithmetic progression $km+l$, $1\leq l\leq k$, $(l,k)=1$, $m=0,1,\ldots,$ and not exceeding $x$, as a function of $N(\sigma,T,\chi)$.
Since $N(\sigma,T,\chi)$ does not increase with $\sigma$ and $N(1,T,\chi)=0$, the purpose of density theorems is to obtain bounds that converge most rapidly to zero as $\sigma\to1$. In turn, these bounds are substantially supplemented by results on the absence of zeros for Dirichlet $L$-functions in neighbourhoods of the straight line $\sigma=1$, obtained using the Hardy–Littlewood–Vinogradov circle method. In this way it has been possible to obtain strong bounds for the amount of even numbers $n\leq x$ that cannot be represented as the sum of two prime numbers.
Yu.V. Linnik obtained the first density theorems providing bounds for $N(\sigma,T,\chi)$ for an individual character $\chi$ and averaged bounds over all characters modulo $a$, given $k$. Subsequent substantial improvements of density theorems were obtained by A.I. Vinogradov and E. Bombieri, who used bounds on $N(\sigma,T,\chi)$ averaged over all moduli $k\leq Q$ and over all primitive characters modulo $a$, given $k$, in proving a theorem on the average distribution of prime numbers in arithmetic progressions (for $Q=\sqrt x/(\ln x)^c$). The Vinogradov–Bombieri theorem enables one to replace the generalized Riemann hypothesis in various classical problems in additive number theory. There are also various other improvements of density theorems.
References
| [1] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
| [2] | H. Davenport, "Multiplicative number theory" , Springer (1980) |
| [3] | A.F. Lavrik, "A survey of Linnik's large sieve and the density theory of zeros of 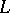 -functions" Russian Math. Surveys , 35 : 2 (1980) pp. 63–76 Uspekhi Mat. Nauk , 35 : 2 (1980) pp. 55–65 -functions" Russian Math. Surveys , 35 : 2 (1980) pp. 63–76 Uspekhi Mat. Nauk , 35 : 2 (1980) pp. 55–65 |
For extra references see Density method. Cf. also Distribution of prime numbers.
For the Vinogradov–Bombieri theorem see Density hypothesis.
References
| [a1] | A. Ivic, "The Riemann zeta-function" , Wiley (1985) |
How to Cite This Entry:
Density theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Density_theorems&oldid=14657
This article was adapted from an original article by B.M. Bredikhin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article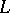 -functions" Russian Math. Surveys , 35 : 2 (1980) pp. 63–76 Uspekhi Mat. Nauk , 35 : 2 (1980) pp. 55–65
-functions" Russian Math. Surveys , 35 : 2 (1980) pp. 63–76 Uspekhi Mat. Nauk , 35 : 2 (1980) pp. 55–65