Difference between revisions of "Ideal"
(Importing text file) |
m (links) |
||
| Line 25: | Line 25: | ||
An ideal of the multiplicative semi-group of a ring may or may not be an ideal of the ring. A semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003058.png" /> is a group if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003059.png" /> has no (left or two-sided) ideal other than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003060.png" />. Thus, the abundance of ideals in a semi-group characterizes the degree to which the semi-group differs from a group. | An ideal of the multiplicative semi-group of a ring may or may not be an ideal of the ring. A semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003058.png" /> is a group if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003059.png" /> has no (left or two-sided) ideal other than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003060.png" />. Thus, the abundance of ideals in a semi-group characterizes the degree to which the semi-group differs from a group. | ||
| − | For a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003061.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003062.png" /> (an algebra over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003063.png" />), an ideal of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003064.png" /> need not be an ideal of the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003065.png" />. For example, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003066.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003067.png" />-algebra with zero multiplication, the set of ideals of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003068.png" /> is the set of subgroups of the additive group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003069.png" />, while the set of ideals of the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003070.png" /> is the set of all subspaces of the vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003071.png" />-space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003072.png" />. However, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003073.png" /> is an algebra with identity, these concepts of an ideal coincide. Therefore many results have identical statements for rings and algebras. | + | For a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003061.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003062.png" /> (an algebra over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003063.png" />), an ideal of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003064.png" /> need not be an ideal of the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003065.png" />. For example, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003066.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003067.png" />-algebra with zero multiplication, the set of ideals of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003068.png" /> is the set of subgroups of the additive group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003069.png" />, while the set of ideals of the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003070.png" /> is the set of all subspaces of the vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003071.png" />-space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003072.png" />. However, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003073.png" /> is an [[unital ring|algebra with identity]], these concepts of an ideal coincide. Therefore many results have identical statements for rings and algebras. |
A ring not having any two-sided ideal is said to be a [[Simple ring|simple ring]]. A ring without proper one-sided ideals is a [[Skew-field|skew-field]]. Left ideals of a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003074.png" /> may also be defined as submodules of the left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003075.png" />-module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003076.png" />. Some properties of rings remain unchanged when right ideals are substituted for left ideals. For example, the [[Jacobson radical|Jacobson radical]] defined in terms of left ideals is the same as the Jacobson radical defined in terms of right ideals. On the other hand, a left Noetherian ring can fail to be right Noetherian. | A ring not having any two-sided ideal is said to be a [[Simple ring|simple ring]]. A ring without proper one-sided ideals is a [[Skew-field|skew-field]]. Left ideals of a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003074.png" /> may also be defined as submodules of the left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003075.png" />-module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003076.png" />. Some properties of rings remain unchanged when right ideals are substituted for left ideals. For example, the [[Jacobson radical|Jacobson radical]] defined in terms of left ideals is the same as the Jacobson radical defined in terms of right ideals. On the other hand, a left Noetherian ring can fail to be right Noetherian. | ||
| − | The study of ideals in commutative rings is an important part of commutative algebra. With every commutative ring with identity one can associate the topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003077.png" /> whose elements are the proper prime ideals of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003078.png" />. There is a one-to-one correspondence between the set of all radicals of ideals of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003079.png" /> and the set of closed subspaces of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003080.png" />. | + | The study of ideals in commutative rings is an important part of commutative algebra. With every commutative [[ring with identity]] one can associate the topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003077.png" /> whose elements are the proper prime ideals of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003078.png" />. There is a one-to-one correspondence between the set of all radicals of ideals of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003079.png" /> and the set of closed subspaces of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003080.png" />. |
The concept of an ideal of a field occurs in commutative algebra, more precisely, that of an ideal of a field relative to a ring. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003081.png" /> is a commutative ring with identity and without zero divisors, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003082.png" /> is the field of fractions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003083.png" />. An ideal of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003084.png" /> is a non-zero subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003085.png" /> that is a subgroup of the additive group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003086.png" /> closed under multiplication by elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003087.png" /> (that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003088.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003089.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003090.png" />) and such that there exists an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003091.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003092.png" />. An ideal is said to be an integral ideal if it is contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003093.png" /> (and then it is an ordinary ideal of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003094.png" />); otherwise it is a [[Fractional ideal|fractional ideal]]. | The concept of an ideal of a field occurs in commutative algebra, more precisely, that of an ideal of a field relative to a ring. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003081.png" /> is a commutative ring with identity and without zero divisors, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003082.png" /> is the field of fractions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003083.png" />. An ideal of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003084.png" /> is a non-zero subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003085.png" /> that is a subgroup of the additive group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003086.png" /> closed under multiplication by elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003087.png" /> (that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003088.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003089.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003090.png" />) and such that there exists an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003091.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003092.png" />. An ideal is said to be an integral ideal if it is contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003093.png" /> (and then it is an ordinary ideal of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050030/i05003094.png" />); otherwise it is a [[Fractional ideal|fractional ideal]]. | ||
Revision as of 16:11, 11 September 2016
A special type of subobject of an algebraic structure. The concept of an ideal first arose in the theory of rings. The name ideal derives from the concept of an ideal number.
For an algebra, a ring or a semi-group 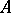 , an ideal
, an ideal 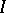 is a subalgebra, subring or sub-semi-group closed under multiplication by elements of
is a subalgebra, subring or sub-semi-group closed under multiplication by elements of 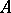 . Here an ideal is said to be a left (or right) ideal if it is closed under multiplication on the left (or right) by elements of
. Here an ideal is said to be a left (or right) ideal if it is closed under multiplication on the left (or right) by elements of 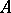 , that is, if
, that is, if
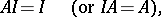 |
where
 |
An ideal that is simultaneously a left ideal and a right ideal (that is, one that is preserved under multiplication by elements of 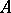 ) is said to be two-sided. These three concepts coincide in the commutative case. Every assertion about left ideals has a corresponding dual assertion about right ideals (subsequent statements will refer only to the "left case" ).
) is said to be two-sided. These three concepts coincide in the commutative case. Every assertion about left ideals has a corresponding dual assertion about right ideals (subsequent statements will refer only to the "left case" ).
Two-sided ideals in rings and algebras play exactly the same role as do normal subgroups (cf. Normal subgroup) in groups. For every homomorphism 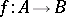 , the kernel
, the kernel 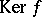 (that is, the set of elements mapped to 0 by
(that is, the set of elements mapped to 0 by 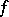 ) is an ideal, and conversely every ideal
) is an ideal, and conversely every ideal 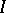 is the kernel of some homomorphism. Moreover, an ideal
is the kernel of some homomorphism. Moreover, an ideal 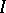 determines a unique congruence (in algebra)
determines a unique congruence (in algebra) 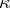 on
on 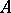 of which it is the zero class, and thus determines the image
of which it is the zero class, and thus determines the image 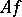 of the homomorphism
of the homomorphism 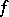 of which it is the kernel uniquely (up to an isomorphism):
of which it is the kernel uniquely (up to an isomorphism): 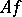 is isomorphic to the quotient ring or quotient algebra
is isomorphic to the quotient ring or quotient algebra 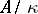 , denoted also by
, denoted also by 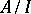 . Ideals of multi-operator groups have similar properties in relation to homomorphisms. In a multi-operator
. Ideals of multi-operator groups have similar properties in relation to homomorphisms. In a multi-operator  -group
-group 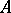 an ideal is defined to be a normal subgroup of its additive group satisfying the following property: For every
an ideal is defined to be a normal subgroup of its additive group satisfying the following property: For every  -ary operator
-ary operator 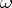 , arbitrary elements
, arbitrary elements 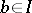 and
and 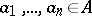 , the relation
, the relation
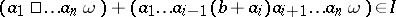 |
holds for 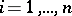 . (This concept reduces to that of a two-sided ideal for rings and algebras.)
. (This concept reduces to that of a two-sided ideal for rings and algebras.)
On the other hand, the two-sided ideals of a semi-group do not give a description of all homomorphic images of the semi-group. If a homomorphism 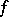 of a semi-group
of a semi-group 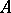 onto a semi-group
onto a semi-group 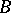 is given, then only in the case where
is given, then only in the case where 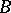 is a semi-group with zero it is possible to associate with
is a semi-group with zero it is possible to associate with 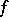 a two-sided ideal in a natural way, namely
a two-sided ideal in a natural way, namely 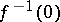 ; however, this association need not determine
; however, this association need not determine 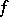 uniquely. Nevertheless, if
uniquely. Nevertheless, if 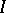 is an ideal of
is an ideal of 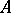 , then among the quotient semi-groups of
, then among the quotient semi-groups of 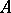 having the class of
having the class of 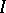 as an element there exists a maximal one, written
as an element there exists a maximal one, written 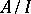 (and called the ideal quotient). The elements of this semi-group are the elements of the set
(and called the ideal quotient). The elements of this semi-group are the elements of the set 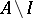 and the ideal
and the ideal 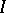 itself, which is the zero in
itself, which is the zero in 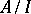 .
.
For an arbitrary subset 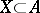 one can define the ideal
one can define the ideal 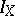 generated by
generated by  as the intersection of all ideals that contain
as the intersection of all ideals that contain 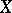 . The set
. The set 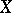 is said to be a basis of the ideal
is said to be a basis of the ideal 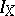 . Different bases can generate one and the same ideal. An ideal generated by a single element is said to be a principal ideal.
. Different bases can generate one and the same ideal. An ideal generated by a single element is said to be a principal ideal.
The intersection, and for semi-groups also the union, of left (two-sided) ideals is again a left (two-sided) ideal. For rings and algebras, the set-theoretical union of ideals need not be an ideal. Let 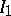 and
and 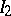 be left or two-sided ideals in a ring (or algebra)
be left or two-sided ideals in a ring (or algebra) 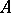 . The sum of the ideals
. The sum of the ideals 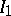 and
and 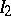 is the ideal
is the ideal 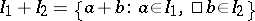 ; it is the smallest ideal of
; it is the smallest ideal of 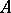 containing
containing 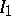 and
and 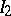 . The set of all (left or two-sided) ideals of a ring (or algebra) forms a lattice under the operations of intersection and taking sums. Many classes of rings and algebras are defined by conditions on their ideals or on the lattice of ideals (see Principal ideal ring; Artinian ring; Noetherian ring).
. The set of all (left or two-sided) ideals of a ring (or algebra) forms a lattice under the operations of intersection and taking sums. Many classes of rings and algebras are defined by conditions on their ideals or on the lattice of ideals (see Principal ideal ring; Artinian ring; Noetherian ring).
An ideal of the multiplicative semi-group of a ring may or may not be an ideal of the ring. A semi-group 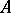 is a group if and only if
is a group if and only if 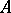 has no (left or two-sided) ideal other than
has no (left or two-sided) ideal other than 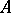 . Thus, the abundance of ideals in a semi-group characterizes the degree to which the semi-group differs from a group.
. Thus, the abundance of ideals in a semi-group characterizes the degree to which the semi-group differs from a group.
For a 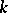 -algebra
-algebra 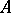 (an algebra over a field
(an algebra over a field 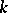 ), an ideal of the ring
), an ideal of the ring 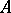 need not be an ideal of the algebra
need not be an ideal of the algebra 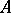 . For example, if
. For example, if 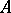 is a
is a 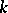 -algebra with zero multiplication, the set of ideals of the ring
-algebra with zero multiplication, the set of ideals of the ring 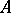 is the set of subgroups of the additive group of
is the set of subgroups of the additive group of 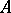 , while the set of ideals of the algebra
, while the set of ideals of the algebra 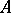 is the set of all subspaces of the vector
is the set of all subspaces of the vector 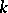 -space
-space 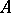 . However, when
. However, when 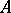 is an algebra with identity, these concepts of an ideal coincide. Therefore many results have identical statements for rings and algebras.
is an algebra with identity, these concepts of an ideal coincide. Therefore many results have identical statements for rings and algebras.
A ring not having any two-sided ideal is said to be a simple ring. A ring without proper one-sided ideals is a skew-field. Left ideals of a ring 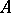 may also be defined as submodules of the left
may also be defined as submodules of the left 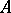 -module
-module 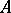 . Some properties of rings remain unchanged when right ideals are substituted for left ideals. For example, the Jacobson radical defined in terms of left ideals is the same as the Jacobson radical defined in terms of right ideals. On the other hand, a left Noetherian ring can fail to be right Noetherian.
. Some properties of rings remain unchanged when right ideals are substituted for left ideals. For example, the Jacobson radical defined in terms of left ideals is the same as the Jacobson radical defined in terms of right ideals. On the other hand, a left Noetherian ring can fail to be right Noetherian.
The study of ideals in commutative rings is an important part of commutative algebra. With every commutative ring with identity one can associate the topological space 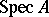 whose elements are the proper prime ideals of
whose elements are the proper prime ideals of 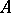 . There is a one-to-one correspondence between the set of all radicals of ideals of
. There is a one-to-one correspondence between the set of all radicals of ideals of 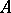 and the set of closed subspaces of
and the set of closed subspaces of 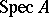 .
.
The concept of an ideal of a field occurs in commutative algebra, more precisely, that of an ideal of a field relative to a ring. Here 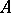 is a commutative ring with identity and without zero divisors, and
is a commutative ring with identity and without zero divisors, and 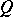 is the field of fractions of
is the field of fractions of 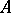 . An ideal of the field
. An ideal of the field 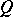 is a non-zero subset
is a non-zero subset 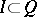 that is a subgroup of the additive group of
that is a subgroup of the additive group of 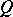 closed under multiplication by elements of
closed under multiplication by elements of 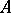 (that is,
(that is, 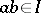 whenever
whenever 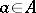 and
and 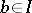 ) and such that there exists an element
) and such that there exists an element 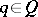 such that
such that 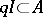 . An ideal is said to be an integral ideal if it is contained in
. An ideal is said to be an integral ideal if it is contained in 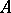 (and then it is an ordinary ideal of
(and then it is an ordinary ideal of 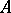 ); otherwise it is a fractional ideal.
); otherwise it is a fractional ideal.
An ideal of a lattice is a non-empty subset 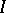 of a lattice such that: 1) if
of a lattice such that: 1) if 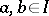 , then
, then 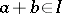 ; and 2) if
; and 2) if 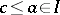 , then
, then 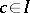 . A dual ideal (or a filter) of a lattice is defined in the dual manner (
. A dual ideal (or a filter) of a lattice is defined in the dual manner (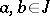 implies
implies 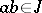 ;
; 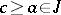 implies
implies 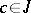 ). The ideals of a lattice also form a lattice under inclusion. A maximal element of the set of all proper ideals of a lattice is called a maximal ideal. If
). The ideals of a lattice also form a lattice under inclusion. A maximal element of the set of all proper ideals of a lattice is called a maximal ideal. If 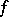 is a homomorphism of a lattice onto a partially ordered set with a zero, then the complete inverse image of the zero is an ideal. It is called the kernel ideal of
is a homomorphism of a lattice onto a partially ordered set with a zero, then the complete inverse image of the zero is an ideal. It is called the kernel ideal of 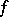 . An ideal
. An ideal 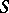 of a lattice
of a lattice 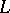 is said to be a standard ideal if for arbitrary
is said to be a standard ideal if for arbitrary 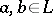 ,
, 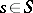 , the inequality
, the inequality  implies that
implies that  , where
, where 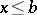 and
and 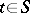 . Every standard ideal is a kernel ideal. A kernel ideal of a relatively complemented lattice (see Lattice with complements) is standard. An ideal
. Every standard ideal is a kernel ideal. A kernel ideal of a relatively complemented lattice (see Lattice with complements) is standard. An ideal 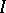 is called a prime ideal if
is called a prime ideal if 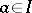 or
or 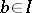 whenever
whenever 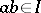 . Each of the following conditions is equivalent to primality for an ideal
. Each of the following conditions is equivalent to primality for an ideal 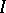 of a lattice
of a lattice 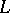 : a) the complement
: a) the complement 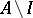 is a filter; or b)
is a filter; or b) 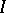 is the complete inverse image of zero under some homomorphism of
is the complete inverse image of zero under some homomorphism of 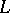 onto a two-element lattice. Every maximal ideal of a distributive lattice is prime.
onto a two-element lattice. Every maximal ideal of a distributive lattice is prime.
The concept of an ideal in a partially ordered set is not in full agreement with the preceding definition. In fact, instead of 1), a stronger condition is required to hold: For every subset of the ideal, the supremum (join) of the set (if it exists) is also in 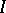 .
.
An ideal object 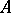 of a category with null morphisms is a subobject
of a category with null morphisms is a subobject 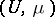 of
of 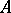 such that
such that 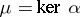 for some morphism
for some morphism 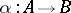 . This ideal can be identified with the set of all monomorphisms that are kernels of some morphism (see also Normal monomorphism). The concept of a co-ideal object of a category is defined in the dual way. The concept of an ideal for
. This ideal can be identified with the set of all monomorphisms that are kernels of some morphism (see also Normal monomorphism). The concept of a co-ideal object of a category is defined in the dual way. The concept of an ideal for  -groups is a special case of that of an ideal object in a category.
-groups is a special case of that of an ideal object in a category.
A left ideal of a category 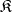 is a class of morphisms containing, with every morphism
is a class of morphisms containing, with every morphism 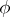 of it, all products
of it, all products 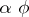 with
with 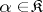 , if these are defined in
, if these are defined in 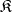 . Right ideals of a category are defined in the dual way. A two-sided ideal is a class of morphisms that is both a left ideal and a right ideal.
. Right ideals of a category are defined in the dual way. A two-sided ideal is a class of morphisms that is both a left ideal and a right ideal.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [2] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
| [3] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [4] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
| [5] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
| [6] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [7] | L.A. Skornyakov, "Elements of lattice theory" , Hindushtan Publ. Comp. (1977) (Translated from Russian) |
| [8] | M.Sh. Tsalenko, E.G. Shul'geifer, "Fundamentals of category theory" , Moscow (1974) (In Russian) |
Comments
There is some disagreement about the correct definition of an ideal 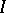 in a partially ordered set
in a partially ordered set 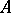 . Instead of the definition given above, some authors would allow
. Instead of the definition given above, some authors would allow 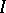 to be an arbitrary lower set (if
to be an arbitrary lower set (if 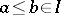 , then
, then 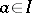 ); others require additionally that
); others require additionally that 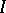 be directed (if
be directed (if 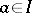 and
and 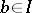 , then there exists a
, then there exists a 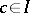 with
with 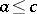 and
and 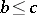 ). The latter definition has the advantage of agreeing with the usual one in the case when
). The latter definition has the advantage of agreeing with the usual one in the case when 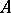 is a lattice (or a join semi-lattice).
is a lattice (or a join semi-lattice).
For a Boolean algebra 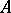 , a subset
, a subset 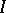 of
of 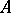 is an ideal in the lattice-theoretic sense if and only if it is an ideal of the Boolean ring
is an ideal in the lattice-theoretic sense if and only if it is an ideal of the Boolean ring 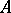 . It was this equivalence which led M.H. Stone [a1] to extend the use of the term "ideal" from rings to lattices. Since then, the study of ideals has played an important role in lattice theory, and particularly in the theory of distributive lattices.
. It was this equivalence which led M.H. Stone [a1] to extend the use of the term "ideal" from rings to lattices. Since then, the study of ideals has played an important role in lattice theory, and particularly in the theory of distributive lattices.
References
| [a1] | M.H. Stone, "Topological representation of distributive lattices and Brouwerian logics" Časopis Pešt. Mat. Fys. , 67 (1937) pp. 1–25 |
| [a2] | P.T. Johnstone, "Stone spaces" , Cambridge Univ. Press (1982) |
| [a3] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
| [a4] | N. Jacobson, "The theory of rings" , Amer. Math. Soc. (1943) |
Ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ideal&oldid=14246