Difference between revisions of "Confocal conics"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
''co-focal curves'' | ''co-focal curves'' | ||
| − | Curves of the second order with common foci. If | + | Curves of the second order with common foci. If $F$ and $F_1$ are two given points in the plane, then through every point of the plane there are one ellipse and one hyperbola that have $F$ and $F_1$ as their foci (Fig. a). |
Every ellipse is orthogonal to every hyperbola confocal with it, that is, they intersect (in four points) at right angles. In a suitable coordinate system, all the confocal ellipses and hyperbolas can be given by the equation | Every ellipse is orthogonal to every hyperbola confocal with it, that is, they intersect (in four points) at right angles. In a suitable coordinate system, all the confocal ellipses and hyperbolas can be given by the equation | ||
| − | + | $$\frac{x^2}{\lambda}+\frac{y^2}{\lambda-c^2}=1,\tag{*}$$ | |
| − | where | + | where $c$ is the distance of the foci from the coordinate origin and $\lambda$ is a variable parameter. If $\lambda>c^2$, this equation defines an ellipse, and if $0<\lambda<c^2$, it defines a hyperbola (if $\lambda<0$, it is an imaginary curve of the second order). If one of the foci tends to infinity, then in the limit one obtains two families of confocal parabolas (Fig. b). |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/c024710a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/c024710a.gif" /> | ||
| Line 17: | Line 18: | ||
Figure: c024710b | Figure: c024710b | ||
| − | Any two parabolas from different families are also orthogonal to one another. Confocal ellipses and hyperbolas can be used to introduce a so-called elliptic coordinate system in the plane as follows. If | + | Any two parabolas from different families are also orthogonal to one another. Confocal ellipses and hyperbolas can be used to introduce a so-called elliptic coordinate system in the plane as follows. If $M(x,y)$ is any point of the plane, then by substituting its coordinates $x$ and $y$ into \ref{*}, one obtains a quadratic equation for $\lambda$; its roots $\lambda_1,\lambda_2$ are the elliptic coordinates of $M$. The confocal ellipses and hyperbolas themselves form the coordinate net of this coordinate system, that is, they are defined by the equations $\lambda_1=\text{const}$ and $\lambda_2=\text{const}$. |
Revision as of 09:01, 29 August 2014
co-focal curves
Curves of the second order with common foci. If $F$ and $F_1$ are two given points in the plane, then through every point of the plane there are one ellipse and one hyperbola that have $F$ and $F_1$ as their foci (Fig. a).
Every ellipse is orthogonal to every hyperbola confocal with it, that is, they intersect (in four points) at right angles. In a suitable coordinate system, all the confocal ellipses and hyperbolas can be given by the equation
$$\frac{x^2}{\lambda}+\frac{y^2}{\lambda-c^2}=1,\tag{*}$$
where $c$ is the distance of the foci from the coordinate origin and $\lambda$ is a variable parameter. If $\lambda>c^2$, this equation defines an ellipse, and if $0<\lambda<c^2$, it defines a hyperbola (if $\lambda<0$, it is an imaginary curve of the second order). If one of the foci tends to infinity, then in the limit one obtains two families of confocal parabolas (Fig. b).
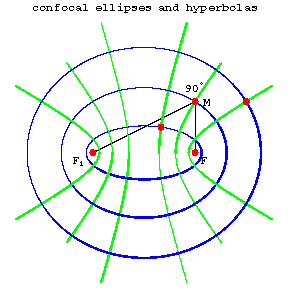
Figure: c024710a
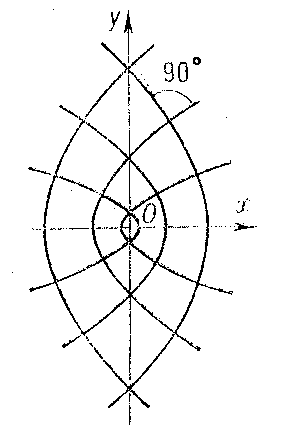
Figure: c024710b
Any two parabolas from different families are also orthogonal to one another. Confocal ellipses and hyperbolas can be used to introduce a so-called elliptic coordinate system in the plane as follows. If $M(x,y)$ is any point of the plane, then by substituting its coordinates $x$ and $y$ into \ref{*}, one obtains a quadratic equation for $\lambda$; its roots $\lambda_1,\lambda_2$ are the elliptic coordinates of $M$. The confocal ellipses and hyperbolas themselves form the coordinate net of this coordinate system, that is, they are defined by the equations $\lambda_1=\text{const}$ and $\lambda_2=\text{const}$.
Comments
References
| [a1] | D.J. Struik, "Lectures on analytic and projective geometry" , Addison-Wesley (1953) pp. 157–160 |
Confocal conics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Confocal_conics&oldid=13848