Dirichlet series

A series of the form

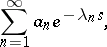(1)

where the 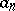are complex coefficients, 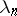, , 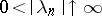are the exponents of the series, and 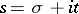is a complex variable. If 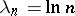, one obtains the so-called ordinary Dirichlet series

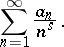The series

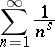represents the Riemann zeta-function for 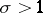. The series

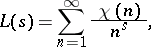where 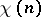is a function, known as a Dirichlet character, were studied by P.G.L. Dirichlet (cf. Dirichlet 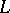-function). Series (1) with arbitrary exponents 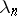are known as general Dirichlet series.

General Dirichlet series with positive exponents.

Let, initially, the 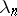be positive numbers. The analogue of the Abel theorem for power series is then valid: If the series (1) converges at a point 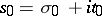, it will converge in the half-plane 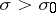, and it will converge uniformly inside an arbitrary angle 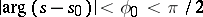. The open domain of convergence of the series is some half-plane 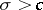. The number is said to be the abscissa of convergence of the Dirichlet series; the straight line 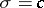is said to be the axis of convergence of the series, and the half-plane 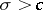is said to be the half-plane of convergence of the series. As well as the half-plane of convergence one also considers the half-plane of absolute convergence of the Dirichlet series, 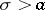: The open domain in which the series converges absolutely (here is the abscissa of absolute convergence). In general, the abscissas of convergence and of absolute convergence are different. But always:

and there exist Dirichlet series for which 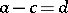. If 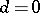, the abscissa of convergence (abscissa of absolute convergence) is computed by the formula

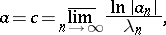which is the analogue of the Cauchy–Hadamard formula. The case 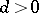is more complicated: If the magnitude

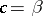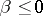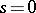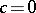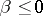is positive, then ; if and the series (1) diverges at the point , then ; if and the series (1) converges at the point , then

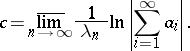The sum of the series, 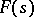, is an analytic function in the half-plane of convergence. If 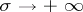, the function 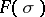asymptotically behaves as the first term of the series, 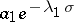(if 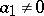). If the sum of the series is zero, then all coefficients of the series are zero. The maximal half-plane 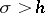in which 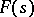is an analytic function is said to be the half-plane of holomorphy of the function 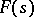, the straight line 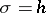is known as the axis of holomorphy and the number 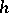is called the abscissa of holomorphy. The inequality 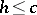is true, and cases when are possible. 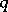Let be the greatest lower bound of the numbers 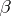for which 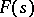is bounded in modulus in the half-plane 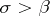(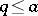). The formula

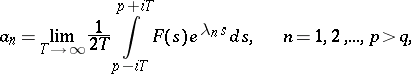is valid, and entails the inequalities

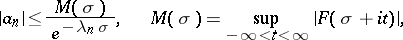which are analogues of the Cauchy inequalities for the coefficients of a power series.

The sum of a Dirichlet series cannot be an arbitrary analytic function in some half-plane 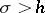; it must, for example, tend to zero if 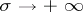. However, the following holds: Whatever the analytic function 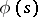in the half-plane 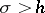, it is possible to find a Dirichlet series (1) such that its sum 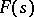will differ from 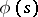by an entire function.

If the sequence of exponents has a density

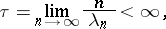the difference between the abscissa of convergence (the abscissas of convergence and of absolute convergence coincide) and the abscissa of holomorphy does not exceed

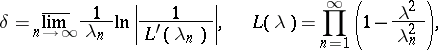and there exist series for which this difference equals 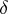. The value of 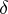may be arbitrary in 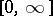; in particular, if 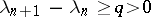, 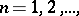then 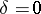. The axis of holomorphy has the following property: On any of its segments of length 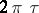the sum of the series has at least one singular point.

If the Dirichlet series (1) converges in the entire plane, its sum 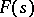is an entire function. Let

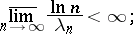then the R-order of the entire function 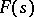(Ritt order) is the magnitude

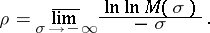Its expression in terms of the coefficients of the series is

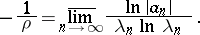One can also introduce the concept of the R-type of a function .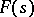

If

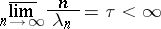and if the function 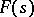is bounded in modulus in a horizontal strip wider than 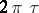, then 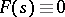(the analogue of one of the Liouville theorems).

Dirichlet series with complex exponents.

For a Dirichlet series

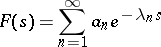(2)

with complex exponents 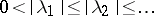, the open domain of absolute convergence is convex. If

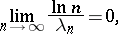the open domains of convergence and absolute convergence coincide. The sum 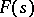of the series (2) is an analytic function in the domain of convergence. The domain of holomorphy of 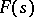is, generally speaking, wider than the domain of convergence of the Dirichlet series (2). If

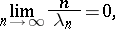then the domain of holomorphy is convex.

Let

let 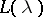be an entire function of exponential type which has simple zeros at the points 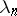, 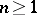; let 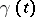be the Borel-associated function to 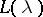(cf. Borel transform); let 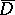be the smallest closed convex set containing all the singular points of 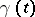, and let

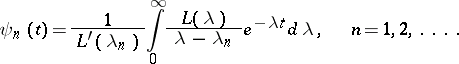Then the functions 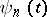are regular outside 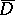, , 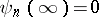and they are bi-orthogonal to the system :

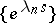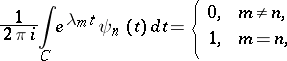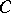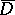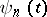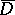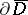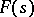where is a closed contour encircling . If the functions are continuous up to the boundary of , the boundary may be taken as . To an arbitrary analytic function in 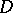(the interior of the domain 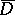) which is continuous in one assigns a series:

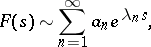(3)

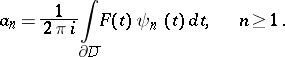For a given bounded convex domain 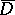it is possible to construct an entire function 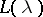with simple zeros 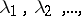such that for any function 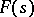analytic in 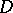and continuous in 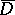the series (3) converges uniformly inside 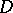to 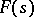. For an analytic functio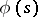n in 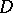(not necessarily continuous in ) it is possible to find an entire function of exponential type zero,

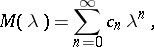and a function 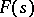analytic in and continuous in 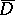, such that

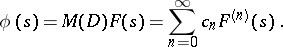Then

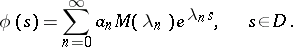The representation of arbitrary analytic functions by Dirichlet series in a domain 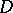was also established in cases when 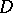is the entire plane or an infinite convex polygonal domain (bounded by a finite number of rectilinear segments).

References

[1]	A.F. Leont'ev, "Exponential series" , Moscow (1976) (In Russian)
[2]	S. Mandelbrojt, "Dirichlet series, principles and methods" , Reidel (1972)

References

[a1]	G.H. Hardy, M. Riesz, "The general theory of Dirichlet series" , Cambridge Univ. Press (1915)