Difference between revisions of "Markov chain, generalized"
From Encyclopedia of Mathematics
(Importing text file) |
(MSC|60J10 Category:Markov chains) |
||
| Line 1: | Line 1: | ||
| + | {{MSC|60J10}} | ||
| + | |||
| + | [[Category:Markov chains]] | ||
| + | |||
A sequence of random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062400/m0624001.png" /> with the properties: | A sequence of random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062400/m0624001.png" /> with the properties: | ||
Revision as of 20:21, 9 March 2012
2020 Mathematics Subject Classification: Primary: 60J10 [MSN][ZBL]
A sequence of random variables 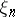 with the properties:
with the properties:
1) the set of values of each 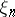 is finite or countable;
is finite or countable;
2) for any  and any
and any 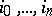 ,
,
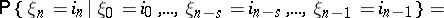 | (*) |
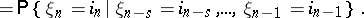 |
A generalized Markov chain satisfying (*) is called  -generalized. For
-generalized. For 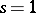 , (*) is the usual Markov property. The study of
, (*) is the usual Markov property. The study of  -generalized Markov chains can be reduced to the study of ordinary Markov chains. Consider the sequence of random variables
-generalized Markov chains can be reduced to the study of ordinary Markov chains. Consider the sequence of random variables 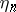 whose values are in one-to-one correspondence with the values of the vector
whose values are in one-to-one correspondence with the values of the vector
 |
The sequence 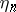 forms an ordinary Markov chain.
forms an ordinary Markov chain.
References
| [1] | J.L. Doob, "Stochastic processes" , Wiley (1953) |
Comments
References
| [a1] | D. Freedman, "Markov chains" , Holden-Day (1975) |
| [a2] | J.G. Kemeny, J.L. Snell, "Finite Markov chains" , v. Nostrand (1960) |
| [a3] | D. Revuz, "Markov chains" , North-Holland (1975) |
| [a4] | V.I. [V.I. Romanovskii] Romanovsky, "Discrete Markov chains" , Wolters-Noordhoff (1970) (Translated from Russian) |
| [a5] | E. Seneta, "Non-negative matrices and Markov chains" , Springer (1981) |
| [a6] | A. Blanc-Lapierre, R. Fortet, "Theory of random functions" , 1–2 , Gordon & Breach (1965–1968) (Translated from French) |
How to Cite This Entry:
Markov chain, generalized. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_chain,_generalized&oldid=13364
Markov chain, generalized. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_chain,_generalized&oldid=13364
This article was adapted from an original article by V.P. Chistyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article