Difference between revisions of "Diagram geometry"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A | + | <!-- |
| + | d1101701.png | ||
| + | $#A+1 = 30 n = 1 | ||
| + | $#C+1 = 30 : ~/encyclopedia/old_files/data/D110/D.1100170 Diagram geometry | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A diagram is like a blueprint describing a possible combination of $ 2 $- | ||
| + | dimensional incidence structures in a higher-dimensional geometry (cf. [[Incidence system|Incidence system]]). In this context, a geometry of rank $ n $ | ||
| + | is a connected [[Graph|graph]] $ \Gamma $ | ||
| + | equipped with an $ n $- | ||
| + | partition $ \Theta $ | ||
| + | such that every maximal clique of $ \Gamma $ | ||
| + | meets every class of $ \Theta $. | ||
| + | The vertices and the adjacency relation of $ \Gamma $ | ||
| + | are the elements and the incidence relation of the geometry, the cliques of $ \Gamma $ | ||
| + | are called flags, the neighbourhood of a non-maximal flag is its residue, the classes of $ \Theta $ | ||
| + | are called types and the type (respectively, rank) of a residue is the set (respectively, number) of types met by it. Given a catalogue of "nice" geometries of rank $ 2 $ | ||
| + | and a symbol for each of those classes, one can compose diagrams of any rank by those symbols. The nodes of a diagram represent types and, by attaching a label to the stroke connecting two types $ i $ | ||
| + | and $ j $ | ||
| + | or by some other convention, one indicates which class the residues of type $ \{ i, j \} $ | ||
| + | should belong to. For instance, a simple stroke | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| Line 11: | Line 37: | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | are normally used to denote, respectively, the class of projective planes (cf. [[Projective plane|Projective plane]]), the class of generalized quadrangles [[#References|[a5]]] (cf. also [[Quadrangle|Quadrangle]]) and the class of generalized digons (generalized digons are the trivial geometry of rank | + | are normally used to denote, respectively, the class of projective planes (cf. [[Projective plane|Projective plane]]), the class of generalized quadrangles [[#References|[a5]]] (cf. also [[Quadrangle|Quadrangle]]) and the class of generalized digons (generalized digons are the trivial geometry of rank $ 2 $, |
| + | where any two elements of different type are incident). The following two diagrams are drawn according to these conventions. | ||
1) | 1) | ||
| Line 21: | Line 48: | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | They both represent geometries of rank | + | They both represent geometries of rank $ 3 $, |
| + | where the residues of type $ \{ 1,2 \} $ | ||
| + | are projective planes and the residues of type $ \{ 1,3 \} $ | ||
| + | are generalized digons. However, the residues of type $ \{ 2,3 \} $ | ||
| + | are projective planes in 1) and generalized quadrangles in 2). The following is a typical problem in diagram geometry: given a diagram of such-and-such type, classify the geometries that fit with it, or at least the finite or flag-transitive such geometries (a geometry $ \Gamma $ | ||
| + | is said to be flag-transitive if $ { \mathop{\rm Aut} } ( \Gamma ) $ | ||
| + | acts transitively on the set of maximal flags of $ \Gamma $). | ||
| + | In the "best" cases the answer is as follows: the geometries under consideration belong to a certain well-known family or, possibly, arise in connection with certain small or sporadic groups. For instance, it is not difficult to prove that $ 3 $- | ||
| + | dimensional projective geometries are the only examples for the above diagram 1). On the other hand, the following has been proved quite recently [[#References|[a7]]]: If $ \Gamma $ | ||
| + | is a flag-transitive example for the diagram 2) and if all rank- $ 1 $ | ||
| + | residues of $ \Gamma $ | ||
| + | are finite of size $ \geq 2 $, | ||
| + | then $ \Gamma $ | ||
| + | is either a classical [[Polar space|polar space]] [[#References|[a6]]] (arising from a non-degenerate alternating, quadratic or Hermitian form of Witt index $ 3 $) | ||
| + | or a uniquely determined very small geometry with $ { \mathop{\rm Aut} } ( \Gamma ) \cong { \mathop{\rm Alt} } ( 7 ) $. | ||
See [[#References|[a3]]] for a survey of related theorems. | See [[#References|[a3]]] for a survey of related theorems. | ||
Revision as of 17:33, 5 June 2020
A diagram is like a blueprint describing a possible combination of $ 2 $-
dimensional incidence structures in a higher-dimensional geometry (cf. Incidence system). In this context, a geometry of rank $ n $
is a connected graph $ \Gamma $
equipped with an $ n $-
partition $ \Theta $
such that every maximal clique of $ \Gamma $
meets every class of $ \Theta $.
The vertices and the adjacency relation of $ \Gamma $
are the elements and the incidence relation of the geometry, the cliques of $ \Gamma $
are called flags, the neighbourhood of a non-maximal flag is its residue, the classes of $ \Theta $
are called types and the type (respectively, rank) of a residue is the set (respectively, number) of types met by it. Given a catalogue of "nice" geometries of rank $ 2 $
and a symbol for each of those classes, one can compose diagrams of any rank by those symbols. The nodes of a diagram represent types and, by attaching a label to the stroke connecting two types $ i $
and $ j $
or by some other convention, one indicates which class the residues of type $ \{ i, j \} $
should belong to. For instance, a simple stroke
a double stroke
and the "null stroke"
are normally used to denote, respectively, the class of projective planes (cf. Projective plane), the class of generalized quadrangles [a5] (cf. also Quadrangle) and the class of generalized digons (generalized digons are the trivial geometry of rank $ 2 $, where any two elements of different type are incident). The following two diagrams are drawn according to these conventions.
1)
2)
They both represent geometries of rank $ 3 $, where the residues of type $ \{ 1,2 \} $ are projective planes and the residues of type $ \{ 1,3 \} $ are generalized digons. However, the residues of type $ \{ 2,3 \} $ are projective planes in 1) and generalized quadrangles in 2). The following is a typical problem in diagram geometry: given a diagram of such-and-such type, classify the geometries that fit with it, or at least the finite or flag-transitive such geometries (a geometry $ \Gamma $ is said to be flag-transitive if $ { \mathop{\rm Aut} } ( \Gamma ) $ acts transitively on the set of maximal flags of $ \Gamma $). In the "best" cases the answer is as follows: the geometries under consideration belong to a certain well-known family or, possibly, arise in connection with certain small or sporadic groups. For instance, it is not difficult to prove that $ 3 $- dimensional projective geometries are the only examples for the above diagram 1). On the other hand, the following has been proved quite recently [a7]: If $ \Gamma $ is a flag-transitive example for the diagram 2) and if all rank- $ 1 $ residues of $ \Gamma $ are finite of size $ \geq 2 $, then $ \Gamma $ is either a classical polar space [a6] (arising from a non-degenerate alternating, quadratic or Hermitian form of Witt index $ 3 $) or a uniquely determined very small geometry with $ { \mathop{\rm Aut} } ( \Gamma ) \cong { \mathop{\rm Alt} } ( 7 ) $.
See [a3] for a survey of related theorems.
References
| [a1] | F. Buekenhout, "Diagrams for geometries and groups" J. Combin. Th. A , 27 (1979) pp. 121–151 |
| [a2] | F. Buekenhout, "Foundations of incidence geometry" F. Buekenhout (ed.) , Handbook of Incidence Geometry , North-Holland (1995) pp. 63–105 |
| [a3] | F. Buekenhout, A. Pasini, "Finite diagram geometries extending buildings" F. Buekenhout (ed.) , Handbook of Incidence Geometry , North-Holland (1995) pp. 1143–1254 |
| [a4] | A. Pasini, "Diagram geometries" , Oxford Univ. Press (1994) |
| [a5] | S.E. Payne, J.A. Thas, "Finite generalized quadrangles" , Pitman (1984) |
| [a6] | J. Tits, "Buildings of spherical type and finite BN-pairs" , Lecture Notes in Mathematics , 386 , Springer (1974) |
| [a7] | S. Yoshiara, "The flag-transitive 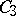 geometries of finite order" J. Algebraic Combinatorics (??) geometries of finite order" J. Algebraic Combinatorics (??) |
Diagram geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diagram_geometry&oldid=12876