Difference between revisions of "H-cobordism"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | h0460102.png | ||
| + | $#A+1 = 149 n = 1 | ||
| + | $#C+1 = 149 : ~/encyclopedia/old_files/data/H046/H.0406010 \BMI h\EMI\AAhcobordism | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A [[Bordism|bordism]] $ ( W; M _ {0} , M _ {1} ) $, | |
| + | where $ W $ | ||
| + | is a compact manifold whose boundary is the disjoint union of closed manifolds $ M _ {0} , M _ {1} $ | ||
| + | which are deformation retracts (cf. [[Deformation retract|Deformation retract]]) of $ W $. | ||
| + | The simplest example is the trivial $ h $- | ||
| + | cobordism | ||
| − | + | $$ | |
| + | ( M \times [ 0, 1]; M \times \{ 0 \} , M \times \{ 1 \} ). | ||
| + | $$ | ||
| − | + | Two manifolds $ M _ {0} $ | |
| + | and $ M _ {1} $ | ||
| + | are said to be $ h $- | ||
| + | cobordant if there is an $ h $- | ||
| + | cobordism $ W $ | ||
| + | joining them. | ||
| − | + | If $ ( W; M _ {0} , M _ {1} ) $ | |
| + | is an $ h $- | ||
| + | cobordism such that $ W $, | ||
| + | $ M _ {0} $, | ||
| + | $ M _ {1} $ | ||
| + | are simply-connected differentiable (or piecewise-linear) manifolds and $ \mathop{\rm dim} W \geq 6 $, | ||
| + | then $ W $ | ||
| + | is diffeomorphic (or piecewise-linearly isomorphic) to $ M _ {0} \times [ 0, 1] $: | ||
| + | $ W \approx M _ {0} \times [ 0, 1] $ | ||
| + | and therefore $ M _ {0} \approx M _ {1} $( | ||
| + | the $ h $- | ||
| + | cobordism theorem [[#References|[4]]]). Thus, proving the isomorphism $ M _ {0} \approx M _ {1} $ | ||
| + | reduces to providing an $ h $- | ||
| + | cobordism, which can be achieved by methods of algebraic topology. For this reason, this theorem is basic in passing from the homotopy classification of simply-connected manifolds to their classification up to a diffeomorphism (or a piecewise-linear isomorphism). Thus, if $ W ^ {n} $, | ||
| + | $ n \geq 6 $, | ||
| + | is a compact differentiable manifold with simply-connected boundary, then it is diffeomorphic to the disc $ D ^ {n} $. | ||
| + | If $ M ^ {n} $, | ||
| + | $ n \geq 5 $, | ||
| + | is a manifold that is homotopy equivalent to the sphere $ S ^ {n} $, | ||
| + | then it is homeomorphic (and even piecewise-linearly isomorphic) to $ S ^ {n} $( | ||
| + | the generalized Poincaré conjecture). | ||
| − | + | The $ h $- | |
| + | cobordism theorem allows one to classify the differentiable structures on the sphere $ S ^ {n} $, | ||
| + | $ n \geq 5 $[[#References|[6]]], and also on the homotopy type of an arbitrary closed simply-connected manifold $ M ^ {n} $, | ||
| + | $ n \geq 5 $[[#References|[1]]]. | ||
| − | + | In the case of an $ h $- | |
| + | cobordism $ ( W; M _ {0} , M _ {1} ) $ | ||
| + | with $ \pi _ {1} W \neq \{ 1 \} $ | ||
| + | there is, in general, no diffeomorphism from $ W $ | ||
| + | to $ M _ {0} \times [ 0, 1] $. | ||
| − | + | All $ h $- | |
| + | cobordisms $ ( W; M _ {0} , M _ {1} ) $ | ||
| + | with $ \mathop{\rm dim} W \geq 6 $ | ||
| + | and $ M _ {0} $ | ||
| + | fixed are classified by a certain Abelian group, namely the [[Whitehead group|Whitehead group]] $ \mathop{\rm Wh} \pi _ {1} $ | ||
| + | of the group $ \pi _ {1} M _ {0} $. | ||
| + | Corresponding to a given $ h $- | ||
| + | cobordism is an element of $ \mathop{\rm Wh} \pi _ {1} $ | ||
| + | that is an invariant of the pair $ ( W, M _ {0} ) $; | ||
| + | it is denoted by $ \tau ( W, M _ {0} ) $ | ||
| + | and is called the torsion (sometimes the [[Whitehead torsion|Whitehead torsion]]) of the given $ h $- | ||
| + | cobordism. If $ \tau ( W, M _ {0} ) = 0 $( | ||
| + | or, equivalently, $ \tau ( W, M _ {1} ) = 0 $), | ||
| + | then the $ h $- | ||
| + | cobordism is called an $ s $- | ||
| + | cobordism. If $ ( W; M _ {0} , M _ {1} ) $ | ||
| + | is an $ h $- | ||
| + | cobordism such that $ \mathop{\rm dim} W \geq 6 $, | ||
| + | then $ \tau ( W, M _ {0} ) $ | ||
| + | vanishes if and only if $ W \approx M _ {0} \times [ 0, 1] $( | ||
| + | the $ s $- | ||
| + | cobordism theorem). The $ h $- | ||
| + | cobordism theorem is a special case of this theorem in view of the fact that $ \mathop{\rm Wh} \{ 1 \} = 0 $. | ||
| + | The $ s $- | ||
| + | cobordism theorem is also true for topological manifolds [[#References|[9]]]. | ||
| − | + | For an $ h $- | |
| + | cobordism $ ( W; M _ {0} , M _ {1} ) $, | ||
| + | the torsion $ \tau ( W, M _ {1} ) $ | ||
| + | is defined along with $ \tau ( W, M _ {0} ) $; | ||
| + | if the given $ h $- | ||
| + | cobordism is orientable, then $ \tau ( W, M _ {0} ) = (- 1) ^ {n - 1 } \tau ^ {*} ( W, M _ {1} ) $, | ||
| + | where $ n = \mathop{\rm dim} W $ | ||
| + | and the element $ \tau ^ {*} $ | ||
| + | is conjugate to $ \tau $ | ||
| + | in the group $ \mathop{\rm Wh} \pi _ {1} $. | ||
| + | In particular, if $ \pi _ {1} $ | ||
| + | is finite and Abelian, $ \tau ^ {*} = \tau $. | ||
| − | If two | + | If two $ h $- |
| + | cobordisms $ ( W; M _ {0} , M _ {1} ) $ | ||
| + | and $ ( W ^ \prime ; M _ {1} , M _ {2} ) $ | ||
| + | are glued along $ M _ {1} $ | ||
| + | to the $ h $- | ||
| + | cobordism $ ( W \cup W ^ \prime ; M _ {0} , M _ {1} ) $, | ||
| + | then | ||
| − | + | $$ | |
| + | \tau ( W \cup W ^ \prime , M _ {0} ) = \ | ||
| + | \tau ( W, M _ {0} ) + \tau ( W ^ \prime , M _ {1} ). | ||
| + | $$ | ||
| − | If two | + | If two copies of $ W $ |
| + | are glued along $ M _ {1} $, | ||
| + | where $ \mathop{\rm dim} W $ | ||
| + | is odd and $ \pi _ {1} = \mathbf Z _ {5} $, | ||
| + | then one obtains an $ h $- | ||
| + | cobordism $ ( 2W; M _ {0} , M _ {0} ^ \prime ) $, | ||
| + | where $ M _ {0} = M _ {0} ^ \prime $ | ||
| + | when there is no diffeomorphism from $ W $ | ||
| + | to $ M _ {0} \times [ 0, 1] $, | ||
| + | that is, when $ M _ {0} \approx M _ {1} $ | ||
| + | does not imply that the $ h $- | ||
| + | cobordism connecting them is trivial. | ||
| − | If | + | If $ M _ {0} $ |
| + | is a closed connected manifold and $ \mathop{\rm dim} M _ {0} \geq 5 $, | ||
| + | then there exists for any $ \tau \in \mathop{\rm Wh} \pi _ {1} M _ {0} $ | ||
| + | an $ h $- | ||
| + | cobordism $ ( W; M _ {0} , M _ {1} ) $ | ||
| + | with $ \tau ( W, M _ {0} ) = \tau $. | ||
| + | If $ ( W; M _ {0} , M _ {1} ) $ | ||
| + | and $ ( W ^ \prime ; M _ {0} , M _ {1} ^ \prime ) $( | ||
| + | with $ \mathop{\rm dim} W \geq 6 $) | ||
| + | have the same torsion $ \tau ( W, M _ {0} ) = \tau ( W ^ \prime , M _ {0} ) $, | ||
| + | then $ W \approx W ^ \prime $ | ||
| + | relative to $ M _ {0} $. | ||
| + | When $ \mathop{\rm dim} M _ {0} $ | ||
| + | is even and $ \pi _ {1} M _ {0} $ | ||
| + | is finite, there is a finite set of distinct manifolds that are $ h $- | ||
| + | cobordant with $ M _ {0} $. | ||
| + | This is not the case when $ \mathop{\rm dim} M _ {0} $ | ||
| + | is odd. | ||
| − | + | If two homotopy-equivalent manifolds $ M _ {1} $ | |
| + | and $ M _ {2} $ | ||
| + | are imbedded in $ \mathbf R ^ {N} $, | ||
| + | with $ N $ | ||
| + | sufficiently large, and their normal bundles are trivial, then $ M _ {1} \times S ^ {N} $ | ||
| + | and $ M _ {2} \times S ^ {N} $ | ||
| + | are $ h $- | ||
| + | cobordant. If, moreover, $ M _ {1} $ | ||
| + | and $ M _ {2} $ | ||
| + | are of the same [[Simple homotopy type|simple homotopy type]], that is, if the torsion of this homotopy equivalence vanishes, then $ M _ {1} \times S ^ {N} \approx M _ {2} \times S ^ {N} $. | ||
| − | + | If $ ( W; M _ {0} , M _ {1} ) $ | |
| + | is an $ h $- | ||
| + | cobordism and $ P $ | ||
| + | is a closed manifold, then there is an $ h $- | ||
| + | cobordism $ ( W \times P; M _ {0} \times P, M _ {1} \times P) $ | ||
| + | with $ \tau ( W \times P, M _ {0} \times P) = \tau ( W, M _ {0} ) \chi ( P) $, | ||
| + | where $ \chi ( P) $ | ||
| + | is the [[Euler characteristic|Euler characteristic]] of $ P $. | ||
| + | If $ \mathop{\rm dim} W \geq 5 $ | ||
| + | and $ P = S ^ {1} $, | ||
| + | then | ||
| − | + | $$ | |
| + | W \times S ^ {1} \approx \ | ||
| + | M _ {0} \times S ^ {1} \times [ 0, 1] \approx \ | ||
| + | M _ {1} \times S ^ {1} \times [ 0, 1]. | ||
| + | $$ | ||
| + | |||
| + | In particular, $ M _ {0} \times S ^ {1} \approx M _ {1} \times S ^ {1} $; | ||
| + | furthermore, two closed manifolds $ M _ {0} $ | ||
| + | and $ M _ {1} $ | ||
| + | of the same dimension $ \geq 5 $ | ||
| + | are $ h $- | ||
| + | cobordant if and only if $ M _ {0} \times \mathbf R ^ {1} \approx M _ {1} \times \mathbf R ^ {1} $. | ||
| + | |||
| + | The $ h $- | ||
| + | cobordism structure has not been completely elucidated for $ n < 6 $( | ||
| + | 1978). Thus there is the following negative result [[#References|[8]]]: There exists an $ h $- | ||
| + | cobordism $ ( W; T ^ {4} , T ^ {4} ) $, | ||
| + | where $ T ^ {4} $ | ||
| + | is the four-dimensional torus, for which there is no diffeomorphism from $ W $ | ||
| + | to $ T ^ {4} \times [ 0, 1] $; | ||
| + | since $ \mathop{\rm Wh} \pi _ {1} T ^ {4} = 0 $, | ||
| + | this means that the $ s $- | ||
| + | cobordism theorem fails for $ n = 5 $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.P. Novikov, "Homotopy-equivalent smooth manifolds I" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''28''' : 2 (1964) pp. 365–474 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Milnor, "Lectures on the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h046/h046010/h046010157.png" />-cobordism theorem" , Princeton Univ. Press (1965)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Milnor, "Whitehead torsion" ''Bull. Amer. Math. Soc.'' , '''72''' (1966) pp. 358–462</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S. Smale, "On the structure of manifolds" ''Amer. J. Math.'' , '''84''' (1962) pp. 387–399</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J. Milnor, "Sommes des variétés différentiables et structures différentiables des sphères" ''Bull. Soc. Math. France'' , '''87''' (1959) pp. 439–444</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M. Kervaire, J. Milnor, "Groups of homotopy spheres I" ''Ann. of Math. (2)'' , '''77''' (1963) pp. 504–537</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B. Mazur, "Relative neighbourhoods and the theorems of Smale" ''Ann. of Math.'' , '''77''' (1963) pp. 232–249</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> L.C. Siebenmann, "Disruption of low-dimensional handlebody theory by Rohlin's theorem" J.C. Cantrell (ed.) C.H. Edwards jr. (ed.) , ''Topology of manifolds'' , Markham (1969) pp. 57–76</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> R. Kirby, L. Siebenmann, "On the triangulation of manifolds and the Hauptvermutung" ''Bull. Amer. Math. Soc.'' , '''75''' (1969) pp. 742–749</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> M.A. Kervaire, "Le théorème de Barden–Mazur–Stallings" M.A. Kervaire (ed.) G. de Rham (ed.) S. Maumary (ed.) , ''Torsion et type simple d'homotopie'' , ''Lect. notes in math.'' , '''48''' , Springer (1967) pp. 83–95</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> R. Thom, "Les classes caractéristiques de Pontryagin des variétés triangulées" , ''Symp. Internac. Topol. Algebr.'' , Univ. Nac. Aut. Mexico & UNESCO (1958) pp. 54–67</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> C.P. Rourke, B.J. Sanderson, "Introduction to piecewise-linear topology" , Springer (1972)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.P. Novikov, "Homotopy-equivalent smooth manifolds I" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''28''' : 2 (1964) pp. 365–474 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Milnor, "Lectures on the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h046/h046010/h046010157.png" />-cobordism theorem" , Princeton Univ. Press (1965)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Milnor, "Whitehead torsion" ''Bull. Amer. Math. Soc.'' , '''72''' (1966) pp. 358–462</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S. Smale, "On the structure of manifolds" ''Amer. J. Math.'' , '''84''' (1962) pp. 387–399</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J. Milnor, "Sommes des variétés différentiables et structures différentiables des sphères" ''Bull. Soc. Math. France'' , '''87''' (1959) pp. 439–444</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M. Kervaire, J. Milnor, "Groups of homotopy spheres I" ''Ann. of Math. (2)'' , '''77''' (1963) pp. 504–537</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B. Mazur, "Relative neighbourhoods and the theorems of Smale" ''Ann. of Math.'' , '''77''' (1963) pp. 232–249</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> L.C. Siebenmann, "Disruption of low-dimensional handlebody theory by Rohlin's theorem" J.C. Cantrell (ed.) C.H. Edwards jr. (ed.) , ''Topology of manifolds'' , Markham (1969) pp. 57–76</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> R. Kirby, L. Siebenmann, "On the triangulation of manifolds and the Hauptvermutung" ''Bull. Amer. Math. Soc.'' , '''75''' (1969) pp. 742–749</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> M.A. Kervaire, "Le théorème de Barden–Mazur–Stallings" M.A. Kervaire (ed.) G. de Rham (ed.) S. Maumary (ed.) , ''Torsion et type simple d'homotopie'' , ''Lect. notes in math.'' , '''48''' , Springer (1967) pp. 83–95</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> R. Thom, "Les classes caractéristiques de Pontryagin des variétés triangulées" , ''Symp. Internac. Topol. Algebr.'' , Univ. Nac. Aut. Mexico & UNESCO (1958) pp. 54–67</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> C.P. Rourke, B.J. Sanderson, "Introduction to piecewise-linear topology" , Springer (1972)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 19:42, 5 June 2020
A bordism $ ( W; M _ {0} , M _ {1} ) $,
where $ W $
is a compact manifold whose boundary is the disjoint union of closed manifolds $ M _ {0} , M _ {1} $
which are deformation retracts (cf. Deformation retract) of $ W $.
The simplest example is the trivial $ h $-
cobordism
$$ ( M \times [ 0, 1]; M \times \{ 0 \} , M \times \{ 1 \} ). $$
Two manifolds $ M _ {0} $ and $ M _ {1} $ are said to be $ h $- cobordant if there is an $ h $- cobordism $ W $ joining them.
If $ ( W; M _ {0} , M _ {1} ) $ is an $ h $- cobordism such that $ W $, $ M _ {0} $, $ M _ {1} $ are simply-connected differentiable (or piecewise-linear) manifolds and $ \mathop{\rm dim} W \geq 6 $, then $ W $ is diffeomorphic (or piecewise-linearly isomorphic) to $ M _ {0} \times [ 0, 1] $: $ W \approx M _ {0} \times [ 0, 1] $ and therefore $ M _ {0} \approx M _ {1} $( the $ h $- cobordism theorem [4]). Thus, proving the isomorphism $ M _ {0} \approx M _ {1} $ reduces to providing an $ h $- cobordism, which can be achieved by methods of algebraic topology. For this reason, this theorem is basic in passing from the homotopy classification of simply-connected manifolds to their classification up to a diffeomorphism (or a piecewise-linear isomorphism). Thus, if $ W ^ {n} $, $ n \geq 6 $, is a compact differentiable manifold with simply-connected boundary, then it is diffeomorphic to the disc $ D ^ {n} $. If $ M ^ {n} $, $ n \geq 5 $, is a manifold that is homotopy equivalent to the sphere $ S ^ {n} $, then it is homeomorphic (and even piecewise-linearly isomorphic) to $ S ^ {n} $( the generalized Poincaré conjecture).
The $ h $- cobordism theorem allows one to classify the differentiable structures on the sphere $ S ^ {n} $, $ n \geq 5 $[6], and also on the homotopy type of an arbitrary closed simply-connected manifold $ M ^ {n} $, $ n \geq 5 $[1].
In the case of an $ h $- cobordism $ ( W; M _ {0} , M _ {1} ) $ with $ \pi _ {1} W \neq \{ 1 \} $ there is, in general, no diffeomorphism from $ W $ to $ M _ {0} \times [ 0, 1] $.
All $ h $- cobordisms $ ( W; M _ {0} , M _ {1} ) $ with $ \mathop{\rm dim} W \geq 6 $ and $ M _ {0} $ fixed are classified by a certain Abelian group, namely the Whitehead group $ \mathop{\rm Wh} \pi _ {1} $ of the group $ \pi _ {1} M _ {0} $. Corresponding to a given $ h $- cobordism is an element of $ \mathop{\rm Wh} \pi _ {1} $ that is an invariant of the pair $ ( W, M _ {0} ) $; it is denoted by $ \tau ( W, M _ {0} ) $ and is called the torsion (sometimes the Whitehead torsion) of the given $ h $- cobordism. If $ \tau ( W, M _ {0} ) = 0 $( or, equivalently, $ \tau ( W, M _ {1} ) = 0 $), then the $ h $- cobordism is called an $ s $- cobordism. If $ ( W; M _ {0} , M _ {1} ) $ is an $ h $- cobordism such that $ \mathop{\rm dim} W \geq 6 $, then $ \tau ( W, M _ {0} ) $ vanishes if and only if $ W \approx M _ {0} \times [ 0, 1] $( the $ s $- cobordism theorem). The $ h $- cobordism theorem is a special case of this theorem in view of the fact that $ \mathop{\rm Wh} \{ 1 \} = 0 $. The $ s $- cobordism theorem is also true for topological manifolds [9].
For an $ h $- cobordism $ ( W; M _ {0} , M _ {1} ) $, the torsion $ \tau ( W, M _ {1} ) $ is defined along with $ \tau ( W, M _ {0} ) $; if the given $ h $- cobordism is orientable, then $ \tau ( W, M _ {0} ) = (- 1) ^ {n - 1 } \tau ^ {*} ( W, M _ {1} ) $, where $ n = \mathop{\rm dim} W $ and the element $ \tau ^ {*} $ is conjugate to $ \tau $ in the group $ \mathop{\rm Wh} \pi _ {1} $. In particular, if $ \pi _ {1} $ is finite and Abelian, $ \tau ^ {*} = \tau $.
If two $ h $- cobordisms $ ( W; M _ {0} , M _ {1} ) $ and $ ( W ^ \prime ; M _ {1} , M _ {2} ) $ are glued along $ M _ {1} $ to the $ h $- cobordism $ ( W \cup W ^ \prime ; M _ {0} , M _ {1} ) $, then
$$ \tau ( W \cup W ^ \prime , M _ {0} ) = \ \tau ( W, M _ {0} ) + \tau ( W ^ \prime , M _ {1} ). $$
If two copies of $ W $ are glued along $ M _ {1} $, where $ \mathop{\rm dim} W $ is odd and $ \pi _ {1} = \mathbf Z _ {5} $, then one obtains an $ h $- cobordism $ ( 2W; M _ {0} , M _ {0} ^ \prime ) $, where $ M _ {0} = M _ {0} ^ \prime $ when there is no diffeomorphism from $ W $ to $ M _ {0} \times [ 0, 1] $, that is, when $ M _ {0} \approx M _ {1} $ does not imply that the $ h $- cobordism connecting them is trivial.
If $ M _ {0} $ is a closed connected manifold and $ \mathop{\rm dim} M _ {0} \geq 5 $, then there exists for any $ \tau \in \mathop{\rm Wh} \pi _ {1} M _ {0} $ an $ h $- cobordism $ ( W; M _ {0} , M _ {1} ) $ with $ \tau ( W, M _ {0} ) = \tau $. If $ ( W; M _ {0} , M _ {1} ) $ and $ ( W ^ \prime ; M _ {0} , M _ {1} ^ \prime ) $( with $ \mathop{\rm dim} W \geq 6 $) have the same torsion $ \tau ( W, M _ {0} ) = \tau ( W ^ \prime , M _ {0} ) $, then $ W \approx W ^ \prime $ relative to $ M _ {0} $. When $ \mathop{\rm dim} M _ {0} $ is even and $ \pi _ {1} M _ {0} $ is finite, there is a finite set of distinct manifolds that are $ h $- cobordant with $ M _ {0} $. This is not the case when $ \mathop{\rm dim} M _ {0} $ is odd.
If two homotopy-equivalent manifolds $ M _ {1} $ and $ M _ {2} $ are imbedded in $ \mathbf R ^ {N} $, with $ N $ sufficiently large, and their normal bundles are trivial, then $ M _ {1} \times S ^ {N} $ and $ M _ {2} \times S ^ {N} $ are $ h $- cobordant. If, moreover, $ M _ {1} $ and $ M _ {2} $ are of the same simple homotopy type, that is, if the torsion of this homotopy equivalence vanishes, then $ M _ {1} \times S ^ {N} \approx M _ {2} \times S ^ {N} $.
If $ ( W; M _ {0} , M _ {1} ) $ is an $ h $- cobordism and $ P $ is a closed manifold, then there is an $ h $- cobordism $ ( W \times P; M _ {0} \times P, M _ {1} \times P) $ with $ \tau ( W \times P, M _ {0} \times P) = \tau ( W, M _ {0} ) \chi ( P) $, where $ \chi ( P) $ is the Euler characteristic of $ P $. If $ \mathop{\rm dim} W \geq 5 $ and $ P = S ^ {1} $, then
$$ W \times S ^ {1} \approx \ M _ {0} \times S ^ {1} \times [ 0, 1] \approx \ M _ {1} \times S ^ {1} \times [ 0, 1]. $$
In particular, $ M _ {0} \times S ^ {1} \approx M _ {1} \times S ^ {1} $; furthermore, two closed manifolds $ M _ {0} $ and $ M _ {1} $ of the same dimension $ \geq 5 $ are $ h $- cobordant if and only if $ M _ {0} \times \mathbf R ^ {1} \approx M _ {1} \times \mathbf R ^ {1} $.
The $ h $- cobordism structure has not been completely elucidated for $ n < 6 $( 1978). Thus there is the following negative result [8]: There exists an $ h $- cobordism $ ( W; T ^ {4} , T ^ {4} ) $, where $ T ^ {4} $ is the four-dimensional torus, for which there is no diffeomorphism from $ W $ to $ T ^ {4} \times [ 0, 1] $; since $ \mathop{\rm Wh} \pi _ {1} T ^ {4} = 0 $, this means that the $ s $- cobordism theorem fails for $ n = 5 $.
References
| [1] | S.P. Novikov, "Homotopy-equivalent smooth manifolds I" Izv. Akad. Nauk SSSR Ser. Mat. , 28 : 2 (1964) pp. 365–474 (In Russian) |
| [2] | J. Milnor, "Lectures on the 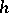 -cobordism theorem" , Princeton Univ. Press (1965) -cobordism theorem" , Princeton Univ. Press (1965) |
| [3] | J. Milnor, "Whitehead torsion" Bull. Amer. Math. Soc. , 72 (1966) pp. 358–462 |
| [4] | S. Smale, "On the structure of manifolds" Amer. J. Math. , 84 (1962) pp. 387–399 |
| [5] | J. Milnor, "Sommes des variétés différentiables et structures différentiables des sphères" Bull. Soc. Math. France , 87 (1959) pp. 439–444 |
| [6] | M. Kervaire, J. Milnor, "Groups of homotopy spheres I" Ann. of Math. (2) , 77 (1963) pp. 504–537 |
| [7] | B. Mazur, "Relative neighbourhoods and the theorems of Smale" Ann. of Math. , 77 (1963) pp. 232–249 |
| [8] | L.C. Siebenmann, "Disruption of low-dimensional handlebody theory by Rohlin's theorem" J.C. Cantrell (ed.) C.H. Edwards jr. (ed.) , Topology of manifolds , Markham (1969) pp. 57–76 |
| [9] | R. Kirby, L. Siebenmann, "On the triangulation of manifolds and the Hauptvermutung" Bull. Amer. Math. Soc. , 75 (1969) pp. 742–749 |
| [10] | M.A. Kervaire, "Le théorème de Barden–Mazur–Stallings" M.A. Kervaire (ed.) G. de Rham (ed.) S. Maumary (ed.) , Torsion et type simple d'homotopie , Lect. notes in math. , 48 , Springer (1967) pp. 83–95 |
| [11] | R. Thom, "Les classes caractéristiques de Pontryagin des variétés triangulées" , Symp. Internac. Topol. Algebr. , Univ. Nac. Aut. Mexico & UNESCO (1958) pp. 54–67 |
| [12] | C.P. Rourke, B.J. Sanderson, "Introduction to piecewise-linear topology" , Springer (1972) |
Comments
For the generalized Poincaré conjecture see also [a1].
References
| [a1] | S. Smale, "Generalized Poincaré's conjecture in dimensions greater than four" Ann. of Math. (2) , 74 (1961) pp. 391–406 |
H-cobordism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=H-cobordism&oldid=11321