Difference between revisions of "Step hyperbolic cross"
m (AUTOMATIC EDIT (latexlist): Replaced 20 formulas out of 22 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
(details) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 22 formulas, 20 were replaced by TEX code.--> | Out of 22 formulas, 20 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
| − | A summation domain of multiple [[Fourier series|Fourier series]]. Like a [[ | + | A summation domain of multiple [[Fourier series|Fourier series]]. Like a [[hyperbolic cross]], it is used for good approximation in the space of functions with bounded mixed derivative (in $L _ { p }$). |
Let $f ( x )$ be an integrable periodic function of $n$ variables defined on $\mathbf{T} ^ { n }$. It has a Fourier series expansion $\sum _ { \mathbf{k} } c_{ \mathbf{k} } e ^ { i \mathbf{kx} }$, $\mathbf{k} = ( k _ { 1 } , \dots , k _ { n } )$, ${\bf x} = ( x _ { 1 } , \ldots , x _ { n } )$, $\mathbf{k} \cdot \mathbf{x} = k _ { 1 } x _ { 1 } + \ldots + k _ { n } x _ { n }$. Unlike in the one-dimensional case, there is no natural ordering of the Fourier coefficients, so the choice of the order of summation is of great importance. | Let $f ( x )$ be an integrable periodic function of $n$ variables defined on $\mathbf{T} ^ { n }$. It has a Fourier series expansion $\sum _ { \mathbf{k} } c_{ \mathbf{k} } e ^ { i \mathbf{kx} }$, $\mathbf{k} = ( k _ { 1 } , \dots , k _ { n } )$, ${\bf x} = ( x _ { 1 } , \ldots , x _ { n } )$, $\mathbf{k} \cdot \mathbf{x} = k _ { 1 } x _ { 1 } + \ldots + k _ { n } x _ { n }$. Unlike in the one-dimensional case, there is no natural ordering of the Fourier coefficients, so the choice of the order of summation is of great importance. | ||
| Line 19: | Line 19: | ||
\begin{equation*} \sum _ { |\mathbf{m \cdot r}| \leq N } \Delta _ { \mathbf{m} } (\, f ) \end{equation*} | \begin{equation*} \sum _ { |\mathbf{m \cdot r}| \leq N } \Delta _ { \mathbf{m} } (\, f ) \end{equation*} | ||
| − | where introduced by B. Mityagin [[#References|[a2]]] for problems in [[Approximation theory|approximation theory]]. They have approximately the same number of harmonics as a hyperbolic cross, but structurally they fit the Marcinkiewicz multiplier theorem (cf. also [[Interpolation of operators|Interpolation of operators]]). It implies that the operator of taking step hyperbolic partial Fourier sums is bounded in each $L ^ { p }$, $1 | + | where introduced by B. Mityagin [[#References|[a2]]] for problems in [[Approximation theory|approximation theory]]. They have approximately the same number of harmonics as a hyperbolic cross, but structurally they fit the Marcinkiewicz multiplier theorem (cf. also [[Interpolation of operators|Interpolation of operators]]). It implies that the operator of taking step hyperbolic partial Fourier sums is bounded in each $L ^ { p }$, $1 < p < \infty$. This means that step hyperbolic partial sums give the best approximation among all hyperbolic cross trigonometric polynomials in $L _ { p }$, $1 < p < \infty$. In the limit cases $p = 1$ and $p = \infty$, the [[Lebesgue constants]] of step hyperbolic partial sums have only logarithmic growth, while for hyperbolic partial Fourier sums they grow as a power of $N$. |
====References==== | ====References==== | ||
| − | <table><tr><td valign="top">[a1]</td> <td valign="top"> E.S. Belinsky, "Lebesgue constants of "step-hyperbolic" partial sums" , ''Theory of Functions and Mappings'' , Nauk. Dumka, Kiev (1989) (In Russian)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> B.S. Mityagin, "Approximation of functions in $L ^ { p }$ and $C$ spaces on the torus" ''Mat. Sb. (N.S.)'' , '''58 (100)''' (1962) pp. 397–414 (In Russian)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> V. Temlyakov, "Approximation of periodic functions" , Nova Sci. (1993)</td></tr></table> | + | <table> |
| + | <tr><td valign="top">[a1]</td> <td valign="top"> E.S. Belinsky, "Lebesgue constants of "step-hyperbolic" partial sums" , ''Theory of Functions and Mappings'' , Nauk. Dumka, Kiev (1989) (In Russian)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> B.S. Mityagin, "Approximation of functions in $L ^ { p }$ and $C$ spaces on the torus" ''Mat. Sb. (N.S.)'' , '''58 (100)''' (1962) pp. 397–414 (In Russian)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> V. Temlyakov, "Approximation of periodic functions" , Nova Sci. (1993)</td></tr> | ||
| + | </table> | ||
Latest revision as of 13:55, 21 January 2024
A summation domain of multiple Fourier series. Like a hyperbolic cross, it is used for good approximation in the space of functions with bounded mixed derivative (in $L _ { p }$).
Let $f ( x )$ be an integrable periodic function of $n$ variables defined on $\mathbf{T} ^ { n }$. It has a Fourier series expansion $\sum _ { \mathbf{k} } c_{ \mathbf{k} } e ^ { i \mathbf{kx} }$, $\mathbf{k} = ( k _ { 1 } , \dots , k _ { n } )$, ${\bf x} = ( x _ { 1 } , \ldots , x _ { n } )$, $\mathbf{k} \cdot \mathbf{x} = k _ { 1 } x _ { 1 } + \ldots + k _ { n } x _ { n }$. Unlike in the one-dimensional case, there is no natural ordering of the Fourier coefficients, so the choice of the order of summation is of great importance.
Let $\mathbf{r} = ( r _ { 1 } , \dots , r _ { n } ) \in \mathbf{R} ^ { n }$ with all coordinates positive, $r_j > 0$. Let
 |
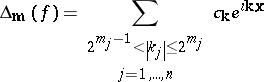be a dyadic "block" of the Fourier series. The step hyperbolic partial sums
\begin{equation*} \sum _ { |\mathbf{m \cdot r}| \leq N } \Delta _ { \mathbf{m} } (\, f ) \end{equation*}
where introduced by B. Mityagin [a2] for problems in approximation theory. They have approximately the same number of harmonics as a hyperbolic cross, but structurally they fit the Marcinkiewicz multiplier theorem (cf. also Interpolation of operators). It implies that the operator of taking step hyperbolic partial Fourier sums is bounded in each $L ^ { p }$, $1 < p < \infty$. This means that step hyperbolic partial sums give the best approximation among all hyperbolic cross trigonometric polynomials in $L _ { p }$, $1 < p < \infty$. In the limit cases $p = 1$ and $p = \infty$, the Lebesgue constants of step hyperbolic partial sums have only logarithmic growth, while for hyperbolic partial Fourier sums they grow as a power of $N$.
References
| [a1] | E.S. Belinsky, "Lebesgue constants of "step-hyperbolic" partial sums" , Theory of Functions and Mappings , Nauk. Dumka, Kiev (1989) (In Russian) |
| [a2] | B.S. Mityagin, "Approximation of functions in $L ^ { p }$ and $C$ spaces on the torus" Mat. Sb. (N.S.) , 58 (100) (1962) pp. 397–414 (In Russian) |
| [a3] | V. Temlyakov, "Approximation of periodic functions" , Nova Sci. (1993) |
Step hyperbolic cross. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Step_hyperbolic_cross&oldid=50237