Namespaces
Variants
Actions

Difference between revisions of "User:Jjtorrens/BancoDePruebas"

From Encyclopedia of Mathematics
Jump to: navigation, search
 
(4 intermediate revisions by the same user not shown)
Line 1: Line 1:
 +
{{MSC|46E35}}
 
{{TEX|part}}
 
{{TEX|part}}
  
Line 4: Line 5:
 
\newcommand{\norm}[1]{\lVert #1\rVert}
 
\newcommand{\norm}[1]{\lVert #1\rVert}
 
\newcommand{\bfl}{\mathbf{l}}$
 
\newcommand{\bfl}{\mathbf{l}}$
 +
A locally summable generalized derivative of a locally summable function (see [[Generalized function|Generalized function]]).
  
−
A space $W^l_p(\Omega)$ of functions $f=f(x)=f(x_1,\ldots,x_n)$ on a set $\Omega\subset\RR^n$ (usually open) such that the $p$-th power of the absolute value of $f$ and of its generalized derivatives (cf. [[Generalized derivative|Generalized derivative]]) up to and including order $l$ are integrable ($1\leq p\leq \infty$).
+
More explicitly, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s0859701.png" /> is an open set in an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s0859702.png" />-dimensional space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s0859703.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s0859704.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s0859705.png" /> are locally summable functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s0859706.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s0859707.png" /> is the Sobolev generalized partial derivative with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s0859708.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s0859709.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597010.png" />:
  
−
The norm of a function $f\in W^l_p(\Omega)$ is given by
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597011.png" /></td> </tr></table>
−
\begin{equation}\label{eq:1}
 
−
  \norm{f}_{W^l_p(\Omega)}=\sum_{\abs{k}\leq l}
 
−
  \norm{f^{(k)}}_{L_p(\Omega)}.
 
−
\end{equation}
 
−
Here
 
−
\begin{equation*}
 
−
  f^{(k)}=\frac{\partial^{\lvert k\rvert}f}{\partial x_1^{k_1}\cdots
 
−
      \partial x_n^{k_n}},\qquad f^{(0)}=f,
 
−
\end{equation*}
 
−
is the generalized partial derivative of $f$ of order
 
−
$\abs{k}=\sum_{j=1}^n k_j$, and
 
−
\begin{equation*}
 
−
  \norm{\psi}_{L_p(\Omega)}
 
−
  =\left( \int_\Omega \abs{\psi(x)}^p\,dx \right)^{1/p}
 
−
  \qquad (1\leq p\leq \infty).
 
−
\end{equation*}
 
  
−
When $p=\infty$, this norm is equal to the essential supremum:
+
if the following equation holds:
−
\begin{equation*}
 
−
  \norm{\psi}_{L_\infty(\Omega)}
 
−
  =\operatorname*{ess sup}_{x\in\Omega}\abs{\psi(x)} \qquad (p=\infty),
 
−
\end{equation*}
 
−
that is, to the greatest lower bound of the set of all $A$ for which
 
−
$A<\abs{\psi(x)}$ on a set of measure zero.
 
  
−
The space $W^l_p(\Omega)$ was defined and first applied in the theory of boundary value problems of mathematical physics by S.L. Sobolev (see [[#References|[1]]], [[#References|[2]]]).
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597012.png" /></td> </tr></table>
  
−
Since its definition involves generalized derivatives rather than ordinary ones, it is complete, that is, it is a [[Banach space|Banach space]].
+
for all infinitely-differentiable functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597013.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597014.png" /> with compact support. The Sobolev generalized derivative is only defined almost-everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597015.png" />.
  
−
$W^l_p(\Omega)$ is considered in conjunction with the linear subspace
+
An equivalent definition is as follows: Suppose that a locally summable function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597016.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597017.png" /> can be modified in such a way that, on a set of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597018.png" />-dimensional measure zero, it will be locally absolutely continuous with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597019.png" /> for almost-all points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597020.png" />, in the sense of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597021.png" />-dimensional measure. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597022.png" /> has an ordinary partial derivative with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597023.png" /> for almost-all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597024.png" />. If the latter is locally summable, then it is called a Sobolev generalized derivative.
−
$W^l_{pc}(\Omega)$ consisting of functions having partial derivatives of order $l$ that are uniformly continuous on $\Omega$. $W^l_{pc}(\Omega)$ has advantages over $W^l_p(\Omega)$, although it is not closed in the metric of $W^l_p(\Omega)$ and is not a complete space. However, for a wide class of domains (those with a Lipschitz boundary, see below) the space $W^l_{pc}(\Omega)$ is dense in $W^l_p(\Omega)$ for all $p$, $1\leq p<\infty$, that is, for such domains the space $W^l_p(\Omega)$ acquires a new property in addition to completeness, in that every function belonging to it can be arbitrarily well approximated in the metric of $W^l_p(\Omega)$ by functions from $W^l_{pc}(\Omega)$.
 
  
−
It is sometimes convenient to replace the expression \eqref{eq:1} for the norm of
+
A third equivalent definition is as follows: Given two functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597025.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597026.png" />, suppose there is a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597027.png" /> of continuously-differentiable functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597028.png" /> such that for any domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597029.png" /> whose closure lies in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597030.png" />,
−
$f\in W^l_p(\Omega)$ by the following:
 
−
\begin{equation}\label{eq:2}
 
−
  \norm{f}^\prime_{W^l_p(\Omega)}=\left( \int_\Omega
 
−
  \sum_{\abs{k}\leq l} \abs{f^{(k)}(x)}^p \,dx \right)^{1/p}
 
−
  \qquad (1\leq p<\infty).
 
−
\end{equation}
 
−
The norm \eqref{eq:2} is equivalent to the norm \eqref{eq:1}, i.e.  
 
−
$c_1 \norm{f}\leq\norm{f}^\prime\leq c_2\norm{f}$,
 
−
where $c_1, c_2>0$ do not depend on $f$. When $p=2$, \eqref{eq:2} is a Hilbert norm, and this fact is widely used in applications.
 
  
−
The boundary $\Gamma$ of a bounded domain $\Omega$ is said to be Lipschitz if for any $x^0\in\Gamma$ there is a rectangular coordinate system $\xi=(\xi_1,\ldots,\xi_n)$ with origin $x^0$ so that the box
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597031.png" /></td> </tr></table>
−
\begin{equation*}
 
−
  \Delta=\{ \xi : \abs{\xi_j}<\delta,\ j=1,\ldots,n \}
 
−
\end{equation*}
 
−
is such that the intersection $\Gamma\cap\Delta$ is described by a function $\xi_n=\psi(\xi')$, with
 
−
\begin{equation*}
 
−
  \xi'=(\xi_1,\ldots,\xi_n)\in\Delta'=\{\abs{\xi_j}<\delta,\ j=1,\ldots,n-1\},
 
−
\end{equation*}
 
−
which satisfies on $\Delta'$ (the projection of $\Delta$ onto the plane $\xi_n=0$) the Lipschitz condition
 
−
\begin{equation*}
 
−
  \abs{\psi(\xi'_1)-\psi(\xi'_2)}\leq M \abs{\xi'_1-\xi'_2},\quad \xi'_1,\xi'_2\in\Delta',
 
−
\end{equation*}
 
−
where the constant $M$ does not depend on the points $\xi'_1,\xi'_2$, and $\abs{\xi}^2=\sum_{j=1}^{n-1}\xi_j^2$. All smooth and many piecewise-smooth boundaries are Lipschitz boundaries.
 
  
−
For a domain with a Lipschitz boundary, \eqref{eq:1} is equivalent to the following:
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597032.png" /></td> </tr></table>
−
\begin{equation*}
 
−
  \norm{f}_{W^l_p(\Omega)}=\norm{f}_{L_p(\Omega)}+\norm{f}'_{w^l_p(\Omega)},
 
−
\end{equation*}
 
−
where
 
−
\begin{equation*}
 
−
  \norm{f}'_{w^l_p(\Omega)}=\sum_{\abs{k}=l}\norm{f^{(k)}}_{L_p(\Omega)}.
 
−
\end{equation*}
 
  
−
One can consider more general anisotropic spaces (classes) $W^\bfl_p(\Omega)$, where $\bfl=(l_1,\ldots,l_n)$ is a positive vector (see [[Imbedding theorems|Imbedding theorems]]). For every such vector $\bfl$ one can define, effectively and to a known extent exhaustively, a class of domains $\mathfrak{M}^{(\bfl)}$ with the property that if $\Omega\in\mathfrak{M}^{(\bfl)}$, then any function $f\in W^\bfl_p(\Omega)$ can be extended to $\R^n$ within the same class. More precisely, it is possible to define a function $\overline{f}$ on $\R^n$ with the properties
+
Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597033.png" /> is the Sobolev generalized derivative of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597034.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597035.png" />.
−
\begin{equation*}
 
−
  \overline{f}(x)=f(x),\quad x\in\Omega,
 
−
  \quad \norm{\overline{f}}_{W^\bfl_p(\R^n)}\leq c \norm{f}_{W^\bfl_p(\R^n)},
 
−
\end{equation*}
 
−
where $c$ does not depend on $f$ (see [[#References|[3]]]).
 
  
−
In virtue of this property, inequalities of the type found in imbedding theorems for functions $f\in W^\bfl_p(\R^n)$ automatically carry over to functions
+
Sobolev generalized derivatives of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597036.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597037.png" /> of higher orders (if they exist) are defined inductively:
−
$f\in W^\bfl_p(\Omega)$, $\Omega\in\mathfrak{M}^{(\bfl)}$.
 
  
−
For vectors $\bfl=(l,\ldots,l)$, the domains $\Omega\in\mathfrak{M}^{(\bfl)}$ have Lipschitz boundaries, and $W^\bfl_p(\Omega)=W^l_p(\Omega)$.
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597038.png" /></td> </tr></table>
  
−
The investigation of the spaces (classes) $W^\bfl_p(\Omega)$
+
They do not depend on the order of differentiation; e.g.,
−
($\Omega\in\mathfrak{M}^{(\bfl)}$) is based on special integral representations for functions belonging to these classes. The first such representation was obtained (see [[#References|[1]]], [[#References|[2]]]) for an isotropic space $W^\bfl_p(\Omega)$ of a domain $\Omega$, star-shaped with respect to some sphere. For the further development of this method see, for example, [[#References|[3]]].
 
  
−
The classes $W^\bfl_p$ and $W^l_p$ can be generalized to the case of fractional $l$, or vectors $\bfl=(l_1,\ldots,l_n)$ with fractional components $l_j$.
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597039.png" /></td> </tr></table>
  
−
The space $W^l_p(\Omega)$ can also be defined for negative integers $l$. Its elements are usually generalized functions, that is, linear functionals $(f,\phi)$ on infinitely-differentiable functions $\phi$ with compact support in $\Omega$.
+
almost-everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085970/s08597040.png" />.
−
 
 
−
By definition, a [[Generalized function|generalized function]] $f$ belongs to the class $W^{-l}_p(\Omega)$ ($l=1,2,\ldots$) if
 
−
\begin{equation*}
 
−
  \norm{f}_{W^{-l}_p(\Omega)}=\sup(f,\phi)
 
−
\end{equation*}
 
−
is finite, where the supremum is taken over all functions $\phi\in W^l_q(\Omega)$ with norm at most one ($1/p+1/q=1$). The functions $f\in W^{-l}_p(\Omega)$ form the space adjoint to the Banach space $W^l_q(\Omega)$.
 
  
 
====References====
 
====References====
−
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  S.L. Sobolev,  "On a theorem of functional analysis"  ''Transl. Amer. Math. Soc. (2)'' , '''34'''  (1963)  pp. 39–68  ''Mat. Sb.'' , '''4'''  (1938)  pp. 471–497</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  S.L. Sobolev,  "Some applications of functional analysis in mathematical physics" , Amer. Math. Soc.  (1963)  (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top">  O.V. Besov,  V.P. Il'in,  S.M. Nikol'skii,  "Integral representations of functions and imbedding theorems" , '''1–2''' , Wiley  (1978)  (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top">  S.M. Nikol'skii,  "Approximation of functions of several variables and imbedding theorems" , Springer (1975)  (Translated from Russian)</TD></TR></table>
+
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  S.L. Sobolev,  "Some applications of functional analysis in mathematical physics" , Amer. Math. Soc.  (1963)  (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  S.M. Nikol'skii,  "A course of mathematical analysis" , '''2''' , MIR (1977)  (Translated from Russian)</TD></TR></table>
  
  
  
 
====Comments====
 
====Comments====
−
 
+
In the Western literature the Sobolev generalized derivative is called the weak or distributional derivative.
  
 
====References====
 
====References====
−
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  V.G. Maz'ja,  "Sobolev spaces" , Springer (1985)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  F. Trèves,  "Basic linear partial differential equations" , Acad. Press (1975)  pp. Sects. 24–26</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top">  R.A. Adams,   "Sobolev spaces" , Acad. Press  (1975)</TD></TR></table>
+
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  L. Schwartz,  "Théorie des distributions" , '''1–2''' , Hermann (1973)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  K. Yosida,  "Functional analysis" , Springer (1980)  pp. Chapt. 8, Sect. 4; 5</TD></TR></table>

Latest revision as of 00:23, 5 May 2012

2020 Mathematics Subject Classification: Primary: 46E35 [MSN][ZBL]


$\newcommand{\abs}[1]{\lvert #1\rvert} \newcommand{\norm}[1]{\lVert #1\rVert} \newcommand{\bfl}{\mathbf{l}}$ A locally summable generalized derivative of a locally summable function (see Generalized function).

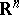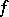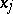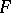More explicitly, if is an open set in an -dimensional space and if and are locally summable functions on , then is the Sobolev generalized partial derivative with respect to of on :

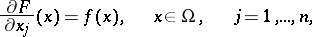if the following equation holds:

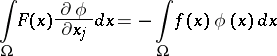for all infinitely-differentiable functions 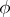on with compact support. The Sobolev generalized derivative is only defined almost-everywhere on .

An equivalent definition is as follows: Suppose that a locally summable functi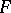on on can be modified in such a way that, on a set of -dimensional measure zero, it will be locally absolutely continuous with respect to 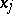for almost-all points 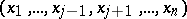, in the sense of the 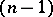-dimensional measure. Then 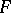has an ordinary partial derivative with respect to 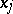for almost-all 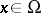. If the latter is locally summable, then it is called a Sobolev generalized derivative.

A third equivalent definition is as follows: Given two functions 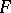and 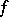, suppose there is a sequence 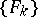of continuously-differentiable functions on such that for any domain 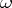whose closure lies in ,

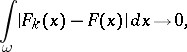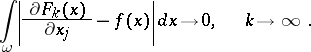Then 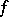is the Sobolev generalized derivative of 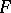on .

Sobolev generalized derivatives of 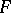on of higher orders (if they exist) are defined inductively:

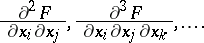They do not depend on the order of differentiation; e.g.,

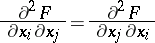almost-everywhere on .

References

[1] S.L. Sobolev, "Some applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian)
[2] S.M. Nikol'skii, "A course of mathematical analysis" , 2 , MIR (1977) (Translated from Russian)


Comments

In the Western literature the Sobolev generalized derivative is called the weak or distributional derivative.

References

[a1] L. Schwartz, "Théorie des distributions" , 1–2 , Hermann (1973)
[a2] K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5
How to Cite This Entry:
Jjtorrens/BancoDePruebas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jjtorrens/BancoDePruebas&oldid=25994
Retrieved from "https://encyclopediaofmath.org/index.php?title=User:Jjtorrens/BancoDePruebas&oldid=26003"