Difference between revisions of "Putnam-Fuglede theorems"
Ulf Rehmann (talk | contribs) m (moved Putnam–Fuglede theorems to Putnam-Fuglede theorems: ascii title) |
(latex details) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 110 formulas, 109 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
''Fuglede–Putnam theorems, Berberian–Putnam–Fuglede theorems'' | ''Fuglede–Putnam theorems, Berberian–Putnam–Fuglede theorems'' | ||
| − | Let | + | Let $H$ denote a [[Hilbert space|Hilbert space]], $B ( H )$ the algebra of operators on $H$ (i.e., bounded linear transformations; cf. [[Linear transformation|Linear transformation]]; [[Operator|Operator]]), $\delta _ { A , B } : B ( H ) \rightarrow B ( H )$ the derivation $\delta _ { A , B } ( X ) = A X - X B$ ($\delta _ { A , A } = \delta _ { A }$; cf. also [[Derivation in a ring|Derivation in a ring]]) and let $\operatorname{ker} \delta _ { A , B } = \{ X \in B ( H ) : \delta _ { A , B } ( X ) = 0 \}$. If $\operatorname { ker }\delta _ { A } \subseteq \operatorname { ker } \delta _ { A ^*}$, then $A$ is normal (cf. [[Normal operator|Normal operator]]; simply choose $X = A$ in $\delta _ { A } ( X )$). The question whether the converse assertion, namely "Is kerdAkerdA* for normal A?" , also holds was raised by J. von Neumann in 1942, and answered in the affirmative in 1950 by B. Fuglede [[#References|[a7]]], p. 349, $\#$45. C.R. Putnam extended the Fuglede theorem to $\operatorname { ker } \delta _ { A , B } \subseteq \operatorname { ker } \delta _ { A^* , B^* }$, for normal $A$ and $B$ [[#References|[a7]]], p. 352, $\#$109, and a beautiful proof of the Putnam–Fuglede theorem was given by M. Rosenblum [[#References|[a7]]], p. 352, $\#$118. Introducing the trick of considering the operators $\hat { A } = A \oplus B$ and $\hat { X } = ( A , B )$ on $\widehat { H } = H \oplus H$, S.K. Berberian [[#References|[a7]]], p. 347, $\#$9, showed that the Putnam–Fuglede theorem indeed follows from the Fuglede theorem. For this reason, Putnam–Fuglede theorems are sometimes also referred to as Berberian–Putnam–Fuglede theorems. |
The Putnam–Fuglede theorem, namely "kerdA,BkerdA*,B* for normal A and B" , has since been considered in a large number of papers, and various generalizations of it have appeared over the past four decades. Broadly speaking, these generalizations fall into the following four types: | The Putnam–Fuglede theorem, namely "kerdA,BkerdA*,B* for normal A and B" , has since been considered in a large number of papers, and various generalizations of it have appeared over the past four decades. Broadly speaking, these generalizations fall into the following four types: | ||
| − | i) where the normality is replaced by a weaker requirement, such as subnormality or | + | i) where the normality is replaced by a weaker requirement, such as subnormality or $p$-hyponormality; |
ii) asymptotic Putnam–Fuglede theorems; | ii) asymptotic Putnam–Fuglede theorems; | ||
| − | iii) Putnam–Fuglede theorems modulo (proper, two-sided) ideals of | + | iii) Putnam–Fuglede theorems modulo (proper, two-sided) ideals of $B ( H )$; and |
| − | iv) Putnam–Fuglede theorems in a | + | iv) Putnam–Fuglede theorems in a $B$-space setting. Before briefly examining some of these, note that there exist subnormal operators $A$ and $B$ for which $\operatorname { ker } \delta _ { A , B } \nsubseteq \operatorname { ker } \delta _ { A ^ { * } , B ^ { * }}$ [[#References|[a7]]], p. 107. This implies that in any generalization of the Putnam–Fuglede theorem to a wider class of operators, the hypotheses on $A$ and $B$ are not symmetric (and that it is more appropriate to think of $A$ and $B ^ { * }$ as being normal in the Putnam–Fuglede theorem). |
==Asymmetric Putnam–Fuglede theorems.== | ==Asymmetric Putnam–Fuglede theorems.== | ||
| − | If | + | If $A$ and $B ^ { * }$ are subnormal operators with normal extensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120170/p12017036.png"/> and $\widehat { B^* } $ on $\widehat { H } = H \oplus H$ (say) and $X \in \operatorname { ker } \delta _ { A , B }$, then $\hat { X } = X \oplus 0 \in \operatorname { ker } \delta _ { \hat{A} , B }$, and it follows that $\hat { X } \in \operatorname { ker } \delta _ { \hat { A } ^ { * } , B ^ { * }}$ and $X \in \operatorname{ker} \delta _ { A^ * , B ^*}$. This asymmetric extension of the Putnam–Fuglede theorem was proved by T. Furuta [[#References|[a6]]] (though an avatar of this result had already appeared in [[#References|[a10]]]). Following a lot of activity during the 1970s and the 1980s ([[#References|[a2]]], [[#References|[a5]]], [[#References|[a6]]], [[#References|[a9]]] list some of the references), it is now (1998) known that $\operatorname { ker } \delta _ { A , B } \subseteq \operatorname { ker } \delta _ { A^* , B^* }$ for $A$ and $B ^ { * }$ belonging to a large number of suitably paired classes of operators, amongst them $p$-hyponormal ($0 < p \leq 1$), $M$-hyponormal, dominant and $k$-quasi-hyponormal classes [[#References|[a5]]]. |
==Asymptotic Putnam–Fuglede theorems.== | ==Asymptotic Putnam–Fuglede theorems.== | ||
| − | Given normal | + | Given normal $A$ and $B$, and a neighbourhood $\mathcal{N} _ { \epsilon}$ of $0$ in some topology (weak operator, strong operator or uniform), does there exist a neighbourhood $\mathcal N _ { \epsilon } ^ { \prime }$ of $0$ in the same topology such that $\delta _ { A , B } ( X ) \in \mathcal{N} _ { \epsilon } ^ { \prime } \Rightarrow \delta _ { A ^ { * } , B ^ { * } } ( X ) \in \mathcal{N}_ { \epsilon }$? The answer to this question is (in general) no, for there exists a normal $A$ and a (non-uniformly bounded) sequence $\{ X _ { n } \}$ of operators such that $\| \delta _ { A } ( X _ { n } ) \| \rightarrow 0$ but $\| \delta _ { A } * ( X _ { n } ) \| \geq 1$ for all $n$ [[#References|[a8]]]. If, however, the sequence $\{ X _ { n } \}$ is uniformly bounded, then the answer is in the affirmative for normal (and subnormal) $A$ and $B ^ { * }$ [[#References|[a2]]] (and indeed, if one limits oneself to the [[Uniform topology|uniform topology]], for a number of classes of operators [[#References|[a5]]], [[#References|[a9]]]). |
==Putnam–Fuglede theorems modulo ideals.== | ==Putnam–Fuglede theorems modulo ideals.== | ||
| − | Say that the Putnam–Fuglede theorem holds modulo an ideal | + | Say that the Putnam–Fuglede theorem holds modulo an ideal $I$ if, given normal operators $A$ and $B$, $\delta _ { A , B } ( X ) \in I$ implies $\delta _ { A ^ * , B^ *} ( X ) \in I$ for all $X \in B ( H )$. The Putnam–Fuglede theorem holds modulo the compacts (simply consider the Putnam–Fuglede theorem in the Calkin algebra), and does not hold modulo the ideal of finite-rank operators. In a remarkable extension of the Putnam–Fuglede theorem to Schatten-von Neumann ideals $\mathcal{C} _ { p }$, $1 \leq p < \infty$ (cf. also [[Calderón couples|Calderón couples]]), G. Weiss proved in [[#References|[a12]]] that $\delta _ { A , B } ( X ) \in \mathcal{C} _ { 2 }$ implies $\delta _ { A^{*} , B ^ { * } } ( X ) \in \mathcal{C} _ { 2 }$. It has since been proved that the Putnam–Fuglede theorem holds modulo $\mathcal{C} _ { p }$ for all $1 < p < \infty$ [[#References|[a1]]], [[#References|[a12]]], and also with normal $A$, $B ^ { * }$ replaced by subnormal $A$, $B ^ { * }$. It is not known if the Putnam–Fuglede theorem holds modulo $\mathcal{C} _ { 1 }$. |
==Banach space formulation of the Putnam–Fuglede theorem.== | ==Banach space formulation of the Putnam–Fuglede theorem.== | ||
| − | Letting | + | Letting $A = a + i b$ and $B = c + i d$, where $a$, $b$, $c$, $d$ are self-adjoint operators such that $a b = b a$ and $c d = d c$ (cf. also [[Self-adjoint operator|Self-adjoint operator]]), the Putnam–Fuglede theorem can be written as |
| − | + | \begin{equation*} ( a + i b ) x = x ( c + i d ) \Leftrightarrow ( a - i b ) x = x ( c - i d ), \end{equation*} | |
or, equivalently, | or, equivalently, | ||
| − | + | \begin{equation*} ( a x - x c ) + i ( b x - x d ) = 0 \end{equation*} | |
| − | + | \begin{equation*} \Updownarrow a x - x c = 0 \text { and } b x - x d = 0, \end{equation*} | |
| − | for all | + | for all $x \in B ( H )$. Defining $\mathcal{A}$ and $\mathcal{B}$ by $\mathcal{A} x = a x - x c$ and $\mathcal{B} x = b x - x d$, it is seen that $\mathcal{A}$ and $\mathcal{B}$ are Hermitian (i. e., the one-parameter groups $e ^ { i t {\cal A}}$ and $e ^ { i t \mathcal{B} }$, $t$ a real number, are groups of isometries on the [[Banach space|Banach space]] $B ( H )$) which commute. The Putnam–Fuglede theorem now says that if $x \in B ( H )$ and $( \mathcal{A} + i \mathcal{B} ) x = 0$, then $\mathcal{A} x = 0 = \mathcal{B} x$. This version of the Putnam–Fuglede theorem has been generalized to the Banach space setting as follows: if $\mathcal{A}$ and $\mathcal{B}$ are commuting Hermitian operators on a complex Banach space $V$, then, given $x \in V$, |
| − | + | \begin{equation*} ( \mathcal{A} + i \mathcal{B} ) x = 0 \Leftrightarrow \mathcal{A} x = 0 = \mathcal{B} x \end{equation*} | |
(see [[#References|[a3]]], [[#References|[a4]]] for more general results). | (see [[#References|[a3]]], [[#References|[a4]]] for more general results). | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> A. Abdessemed, E.B. Davies, "Some commutator estimates in the Schatten classes" ''J. London Math. Soc.'' , '''39''' (1989) pp. 299–308</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> S.T.M. Ackermans, S.J.L. Eijndhoven, F.J.L. Martens, "On almost commuting operators" ''Nederl. Akad. Wetensch. Proc. Ser. A'' , '''86''' (1983) pp. 389–391</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> K. Boydazhiev, "Commuting $C_o $ groups and the Fuglede–Putnam theorem" ''Studia Math.'' , '''81''' (1985) pp. 303–306</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> M.J. Crabb, P.G. Spain, "Commutators and normal operators" ''Glasgow Math. J.'' , '''18''' (1977) pp. 197–198</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> B.P. Duggal, "On generalised Putnam–Fuglede theorems" ''Monatsh. Math.'' , '''107''' (1989) pp. 309–332 (See also: On quasi-similar hyponormal operators, Integral Eq. Oper. Th. 26 (1996), 338-345)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> T. Furuta, "On relaxation of normality in the Fuglede–Putnam theorem" ''Proc. Amer. Math. Soc.'' , '''77''' (1979) pp. 324–328</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> P.R. Halmos, "A Hilbert space problem book" , Springer (1982)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> B.E. Johnson, J.P. Williams, "The range of a normal derivation" ''Pacific J. Math.'' , '''58''' (1975) pp. 105–122</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> M. Radjabalipour, "An extension of Putnam–Fuglede theorem for hyponormal operators" ''Math. Z.'' , '''194''' (1987) pp. 117–120</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> H. Radjavi, P. Rosenthal, "On roots of normal operators" ''J. Math. Anal. Appl.'' , '''34''' (1971) pp. 653–664</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> V. Shulman, "Some remarks on the Fuglede–Weiss Theorem" ''Bull. London Math. Soc.'' , '''28''' (1996) pp. 385–392</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> G. Weiss, "The Fuglede commutativity theorem modulo the Hilbert–Schmidt class and generating functions I" ''Trans. Amer. Math. Soc.'' , '''246''' (1978) pp. 193–209 (See also: II, J. Operator Th. 5 (1981), 3-16)</td></tr> |
| + | </table> | ||
Latest revision as of 07:43, 27 January 2024
Fuglede–Putnam theorems, Berberian–Putnam–Fuglede theorems
Let $H$ denote a Hilbert space, $B ( H )$ the algebra of operators on $H$ (i.e., bounded linear transformations; cf. Linear transformation; Operator), $\delta _ { A , B } : B ( H ) \rightarrow B ( H )$ the derivation $\delta _ { A , B } ( X ) = A X - X B$ ($\delta _ { A , A } = \delta _ { A }$; cf. also Derivation in a ring) and let $\operatorname{ker} \delta _ { A , B } = \{ X \in B ( H ) : \delta _ { A , B } ( X ) = 0 \}$. If $\operatorname { ker }\delta _ { A } \subseteq \operatorname { ker } \delta _ { A ^*}$, then $A$ is normal (cf. Normal operator; simply choose $X = A$ in $\delta _ { A } ( X )$). The question whether the converse assertion, namely "Is kerdAkerdA* for normal A?" , also holds was raised by J. von Neumann in 1942, and answered in the affirmative in 1950 by B. Fuglede [a7], p. 349, $\#$45. C.R. Putnam extended the Fuglede theorem to $\operatorname { ker } \delta _ { A , B } \subseteq \operatorname { ker } \delta _ { A^* , B^* }$, for normal $A$ and $B$ [a7], p. 352, $\#$109, and a beautiful proof of the Putnam–Fuglede theorem was given by M. Rosenblum [a7], p. 352, $\#$118. Introducing the trick of considering the operators $\hat { A } = A \oplus B$ and $\hat { X } = ( A , B )$ on $\widehat { H } = H \oplus H$, S.K. Berberian [a7], p. 347, $\#$9, showed that the Putnam–Fuglede theorem indeed follows from the Fuglede theorem. For this reason, Putnam–Fuglede theorems are sometimes also referred to as Berberian–Putnam–Fuglede theorems.
The Putnam–Fuglede theorem, namely "kerdA,BkerdA*,B* for normal A and B" , has since been considered in a large number of papers, and various generalizations of it have appeared over the past four decades. Broadly speaking, these generalizations fall into the following four types:
i) where the normality is replaced by a weaker requirement, such as subnormality or $p$-hyponormality;
ii) asymptotic Putnam–Fuglede theorems;
iii) Putnam–Fuglede theorems modulo (proper, two-sided) ideals of $B ( H )$; and
iv) Putnam–Fuglede theorems in a $B$-space setting. Before briefly examining some of these, note that there exist subnormal operators $A$ and $B$ for which $\operatorname { ker } \delta _ { A , B } \nsubseteq \operatorname { ker } \delta _ { A ^ { * } , B ^ { * }}$ [a7], p. 107. This implies that in any generalization of the Putnam–Fuglede theorem to a wider class of operators, the hypotheses on $A$ and $B$ are not symmetric (and that it is more appropriate to think of $A$ and $B ^ { * }$ as being normal in the Putnam–Fuglede theorem).
Asymmetric Putnam–Fuglede theorems.
If $A$ and $B ^ { * }$ are subnormal operators with normal extensions 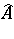 and $\widehat { B^* } $ on $\widehat { H } = H \oplus H$ (say) and $X \in \operatorname { ker } \delta _ { A , B }$, then $\hat { X } = X \oplus 0 \in \operatorname { ker } \delta _ { \hat{A} , B }$, and it follows that $\hat { X } \in \operatorname { ker } \delta _ { \hat { A } ^ { * } , B ^ { * }}$ and $X \in \operatorname{ker} \delta _ { A^ * , B ^*}$. This asymmetric extension of the Putnam–Fuglede theorem was proved by T. Furuta [a6] (though an avatar of this result had already appeared in [a10]). Following a lot of activity during the 1970s and the 1980s ([a2], [a5], [a6], [a9] list some of the references), it is now (1998) known that $\operatorname { ker } \delta _ { A , B } \subseteq \operatorname { ker } \delta _ { A^* , B^* }$ for $A$ and $B ^ { * }$ belonging to a large number of suitably paired classes of operators, amongst them $p$-hyponormal ($0 < p \leq 1$), $M$-hyponormal, dominant and $k$-quasi-hyponormal classes [a5].
and $\widehat { B^* } $ on $\widehat { H } = H \oplus H$ (say) and $X \in \operatorname { ker } \delta _ { A , B }$, then $\hat { X } = X \oplus 0 \in \operatorname { ker } \delta _ { \hat{A} , B }$, and it follows that $\hat { X } \in \operatorname { ker } \delta _ { \hat { A } ^ { * } , B ^ { * }}$ and $X \in \operatorname{ker} \delta _ { A^ * , B ^*}$. This asymmetric extension of the Putnam–Fuglede theorem was proved by T. Furuta [a6] (though an avatar of this result had already appeared in [a10]). Following a lot of activity during the 1970s and the 1980s ([a2], [a5], [a6], [a9] list some of the references), it is now (1998) known that $\operatorname { ker } \delta _ { A , B } \subseteq \operatorname { ker } \delta _ { A^* , B^* }$ for $A$ and $B ^ { * }$ belonging to a large number of suitably paired classes of operators, amongst them $p$-hyponormal ($0 < p \leq 1$), $M$-hyponormal, dominant and $k$-quasi-hyponormal classes [a5].
Asymptotic Putnam–Fuglede theorems.
Given normal $A$ and $B$, and a neighbourhood $\mathcal{N} _ { \epsilon}$ of $0$ in some topology (weak operator, strong operator or uniform), does there exist a neighbourhood $\mathcal N _ { \epsilon } ^ { \prime }$ of $0$ in the same topology such that $\delta _ { A , B } ( X ) \in \mathcal{N} _ { \epsilon } ^ { \prime } \Rightarrow \delta _ { A ^ { * } , B ^ { * } } ( X ) \in \mathcal{N}_ { \epsilon }$? The answer to this question is (in general) no, for there exists a normal $A$ and a (non-uniformly bounded) sequence $\{ X _ { n } \}$ of operators such that $\| \delta _ { A } ( X _ { n } ) \| \rightarrow 0$ but $\| \delta _ { A } * ( X _ { n } ) \| \geq 1$ for all $n$ [a8]. If, however, the sequence $\{ X _ { n } \}$ is uniformly bounded, then the answer is in the affirmative for normal (and subnormal) $A$ and $B ^ { * }$ [a2] (and indeed, if one limits oneself to the uniform topology, for a number of classes of operators [a5], [a9]).
Putnam–Fuglede theorems modulo ideals.
Say that the Putnam–Fuglede theorem holds modulo an ideal $I$ if, given normal operators $A$ and $B$, $\delta _ { A , B } ( X ) \in I$ implies $\delta _ { A ^ * , B^ *} ( X ) \in I$ for all $X \in B ( H )$. The Putnam–Fuglede theorem holds modulo the compacts (simply consider the Putnam–Fuglede theorem in the Calkin algebra), and does not hold modulo the ideal of finite-rank operators. In a remarkable extension of the Putnam–Fuglede theorem to Schatten-von Neumann ideals $\mathcal{C} _ { p }$, $1 \leq p < \infty$ (cf. also Calderón couples), G. Weiss proved in [a12] that $\delta _ { A , B } ( X ) \in \mathcal{C} _ { 2 }$ implies $\delta _ { A^{*} , B ^ { * } } ( X ) \in \mathcal{C} _ { 2 }$. It has since been proved that the Putnam–Fuglede theorem holds modulo $\mathcal{C} _ { p }$ for all $1 < p < \infty$ [a1], [a12], and also with normal $A$, $B ^ { * }$ replaced by subnormal $A$, $B ^ { * }$. It is not known if the Putnam–Fuglede theorem holds modulo $\mathcal{C} _ { 1 }$.
Banach space formulation of the Putnam–Fuglede theorem.
Letting $A = a + i b$ and $B = c + i d$, where $a$, $b$, $c$, $d$ are self-adjoint operators such that $a b = b a$ and $c d = d c$ (cf. also Self-adjoint operator), the Putnam–Fuglede theorem can be written as
\begin{equation*} ( a + i b ) x = x ( c + i d ) \Leftrightarrow ( a - i b ) x = x ( c - i d ), \end{equation*}
or, equivalently,
\begin{equation*} ( a x - x c ) + i ( b x - x d ) = 0 \end{equation*}
\begin{equation*} \Updownarrow a x - x c = 0 \text { and } b x - x d = 0, \end{equation*}
for all $x \in B ( H )$. Defining $\mathcal{A}$ and $\mathcal{B}$ by $\mathcal{A} x = a x - x c$ and $\mathcal{B} x = b x - x d$, it is seen that $\mathcal{A}$ and $\mathcal{B}$ are Hermitian (i. e., the one-parameter groups $e ^ { i t {\cal A}}$ and $e ^ { i t \mathcal{B} }$, $t$ a real number, are groups of isometries on the Banach space $B ( H )$) which commute. The Putnam–Fuglede theorem now says that if $x \in B ( H )$ and $( \mathcal{A} + i \mathcal{B} ) x = 0$, then $\mathcal{A} x = 0 = \mathcal{B} x$. This version of the Putnam–Fuglede theorem has been generalized to the Banach space setting as follows: if $\mathcal{A}$ and $\mathcal{B}$ are commuting Hermitian operators on a complex Banach space $V$, then, given $x \in V$,
\begin{equation*} ( \mathcal{A} + i \mathcal{B} ) x = 0 \Leftrightarrow \mathcal{A} x = 0 = \mathcal{B} x \end{equation*}
(see [a3], [a4] for more general results).
References
| [a1] | A. Abdessemed, E.B. Davies, "Some commutator estimates in the Schatten classes" J. London Math. Soc. , 39 (1989) pp. 299–308 |
| [a2] | S.T.M. Ackermans, S.J.L. Eijndhoven, F.J.L. Martens, "On almost commuting operators" Nederl. Akad. Wetensch. Proc. Ser. A , 86 (1983) pp. 389–391 |
| [a3] | K. Boydazhiev, "Commuting $C_o $ groups and the Fuglede–Putnam theorem" Studia Math. , 81 (1985) pp. 303–306 |
| [a4] | M.J. Crabb, P.G. Spain, "Commutators and normal operators" Glasgow Math. J. , 18 (1977) pp. 197–198 |
| [a5] | B.P. Duggal, "On generalised Putnam–Fuglede theorems" Monatsh. Math. , 107 (1989) pp. 309–332 (See also: On quasi-similar hyponormal operators, Integral Eq. Oper. Th. 26 (1996), 338-345) |
| [a6] | T. Furuta, "On relaxation of normality in the Fuglede–Putnam theorem" Proc. Amer. Math. Soc. , 77 (1979) pp. 324–328 |
| [a7] | P.R. Halmos, "A Hilbert space problem book" , Springer (1982) |
| [a8] | B.E. Johnson, J.P. Williams, "The range of a normal derivation" Pacific J. Math. , 58 (1975) pp. 105–122 |
| [a9] | M. Radjabalipour, "An extension of Putnam–Fuglede theorem for hyponormal operators" Math. Z. , 194 (1987) pp. 117–120 |
| [a10] | H. Radjavi, P. Rosenthal, "On roots of normal operators" J. Math. Anal. Appl. , 34 (1971) pp. 653–664 |
| [a11] | V. Shulman, "Some remarks on the Fuglede–Weiss Theorem" Bull. London Math. Soc. , 28 (1996) pp. 385–392 |
| [a12] | G. Weiss, "The Fuglede commutativity theorem modulo the Hilbert–Schmidt class and generating functions I" Trans. Amer. Math. Soc. , 246 (1978) pp. 193–209 (See also: II, J. Operator Th. 5 (1981), 3-16) |
Putnam-Fuglede theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Putnam-Fuglede_theorems&oldid=22959