Difference between revisions of "Involution algebra"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | i0525201.png | ||
| + | $#A+1 = 134 n = 1 | ||
| + | $#C+1 = 134 : ~/encyclopedia/old_files/data/I052/I.0502520 Involution algebra, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''algebra with involution'' | ''algebra with involution'' | ||
| − | An algebra | + | An algebra $ E $ |
| + | over the field of complex numbers endowed with an [[Involution|involution]] $ x \mapsto x ^ {*} $, | ||
| + | $ x \in E $. | ||
| + | Some examples are: the algebra of continuous functions on a compact set, in which the involution sends any function to its complex conjugate; the algebra of bounded linear operators on a Hilbert space, in which the involution sends any operator to its adjoint; the [[Group algebra of a locally compact group|group algebra of a locally compact group]]; and the algebra of measures on a locally compact group. The element $ x ^ {*} \in E $ | ||
| + | is called the conjugate, or adjoint, of $ x $. | ||
| + | An element $ x \in E $ | ||
| + | is called self-adjoint, or Hermitian, if $ x ^ {*} = x $, | ||
| + | and normal if $ x ^ {*} x = x x ^ {*} $. | ||
| + | If $ E $ | ||
| + | contains a unit element 1, then an element $ x \in E $ | ||
| + | such that $ x ^ {*} x = x x ^ {*} = 1 $ | ||
| + | is called unitary. The set $ E _ {h} $ | ||
| + | of Hermitian elements of $ E $ | ||
| + | is a real vector subspace of $ E $, | ||
| + | and any $ x \in E $ | ||
| + | can be uniquely written in the form $ x = x _ {1} + i x _ {2} $, | ||
| + | where $ x _ {1} , x _ {2} \in E _ {h} $. | ||
| + | In this case $ x \in E $ | ||
| + | is normal if and only if $ x _ {1} $ | ||
| + | and $ x _ {2} $ | ||
| + | commute. Every element of the form $ x ^ {*} x $ | ||
| + | is Hermitian, and so is the unit element. If $ x $ | ||
| + | is invertible, then so is $ x ^ {*} $, | ||
| + | and $ ( x ^ {*} ) ^ {-} 1 = ( x ^ {-} 1 ) ^ {*} $. | ||
| + | The spectrum of any Hermitian element (cf. [[Spectrum of an element|Spectrum of an element]]) is symmetric about the real axis. An involution algebra $ E $ | ||
| + | is called a total involution algebra if the spectrum of any element of the form $ x ^ {*} x $, | ||
| + | $ x \in E $, | ||
| + | is contained in the set of non-negative real numbers. Examples of total involution algebras are: the involution algebra of continuous functions on a compact set; the involution algebra of bounded linear operators on a Hilbert space; and group algebras of compact and commutative locally compact groups. The group algebras of non-compact semi-simple Lie groups are not total involution algebras. A commutative involution algebra $ E $ | ||
| + | is a total involution algebra if and only if all its maximal ideals are symmetric, or if and only if all characters of $ E $ | ||
| + | are Hermitian. Every [[C*-algebra| $ C ^ {*} $- | ||
| + | algebra]] is a total involution algebra. | ||
| − | A subset | + | A subset $ M $ |
| + | of an involution algebra $ E $ | ||
| + | is called an involution set if $ x ^ {*} \in M $ | ||
| + | for all $ x \in M $. | ||
| + | A mapping $ \phi : E \rightarrow F $ | ||
| + | of involution algebras is called an involution mapping if $ \phi ( x) ^ {*} = \phi ( x ^ {*} ) $ | ||
| + | for all $ x \in E $. | ||
| + | The kernel of an involution homomorphism of involution algebras is a symmetric two-sided ideal. Every symmetric one-sided ideal is two-sided and the quotient algebra of an involution algebra by a symmetric ideal admits the structure of an involution algebra in a natural way. The radical (cf. [[Radical of rings and algebras|Radical of rings and algebras]]) of an involution algebra is a symmetric ideal. An involution subalgebra $ F $ | ||
| + | of an involution algebra $ E $ | ||
| + | is an involution algebra. Let $ \widetilde{E} $ | ||
| + | be the direct sum of an involution algebra $ E $ | ||
| + | and the field $ \mathbf C $, | ||
| + | in which the linear operations and the involution are defined componentwise and the multiplication is given by | ||
| − | + | $$ | |
| + | \{ x , \lambda \} \{ y , \mu \} = \ | ||
| + | \{ x y + \lambda y + \mu x , \lambda \mu \} | ||
| + | $$ | ||
| − | for all | + | for all $ \lambda , \mu \in \mathbf C $, |
| + | $ x , y \in E $. | ||
| + | Then $ \widetilde{E} $ | ||
| + | is an involution algebra with a unit element. | ||
| − | A linear functional | + | A linear functional $ f $ |
| + | on an involution algebra is called Hermitian if $ f ( x ^ {*} ) = \overline{ {f ( x) }}\; $ | ||
| + | for all $ x \in E $, | ||
| + | and positive if $ f ( x ^ {*} x ) \geq 0 $ | ||
| + | for all $ x \in E $. | ||
| + | The set $ E _ {h} ^ \prime $ | ||
| + | of Hermitian linear functionals on $ E $ | ||
| + | is a real vector subspace of $ E ^ \prime $, | ||
| + | the dual of $ E $, | ||
| + | and $ E ^ \prime $ | ||
| + | is the direct sum of the subspaces $ E _ {h} ^ \prime $ | ||
| + | and $ i E _ {h} ^ \prime $. | ||
| + | If $ E $ | ||
| + | has a unit 1, then every positive functional $ f $ | ||
| + | on $ E $ | ||
| + | is Hermitian and $ | f ( x) | ^ {2} \leq f ( 1) f ( x ^ {*} x ) $ | ||
| + | for all $ x \in E $. | ||
| + | If $ f $ | ||
| + | is a positive functional on an involution algebra $ E $, | ||
| + | then $ f ( y ^ {*} x ) = f ( x ^ {*} y ) $ | ||
| + | and $ | f ( y ^ {*} x ) | ^ {2} \leq f ( y ^ {*} y) f( x ^ {*} x ) $ | ||
| + | for all $ x , y \in E $. | ||
| − | Let | + | Let $ E $ |
| + | be an involution algebra equipped with a norm making $ E $ | ||
| + | into a [[Normed algebra|normed algebra]] and satisfying the condition $ \| x ^ {*} \| = \| x \| $ | ||
| + | for all $ x \in E $. | ||
| + | Then $ E $ | ||
| + | is called a normed algebra with involution. If $ E $ | ||
| + | is complete with respect to this norm, then $ E $ | ||
| + | is called a Banach algebra with involution. Every normed algebra with involution $ E $ | ||
| + | can be imbedded in a Banach algebra with involution $ \overline{E}\; $ | ||
| + | containing $ E $ | ||
| + | as a dense involution subalgebra. $ \overline{E}\; $ | ||
| + | is uniquely defined up to an isometric involution isomorphism. $ \overline{E}\; $ | ||
| + | is called the completion of $ E $. | ||
| + | If $ E $ | ||
| + | is a Banach algebra with involution having an approximate identity, then every positive linear functional $ f $ | ||
| + | on $ E $ | ||
| + | is continuous and can be extended to a positive linear functional on $ \overline{E}\; $. | ||
| + | If $ E $ | ||
| + | has a unit 1 and $ \| 1 \| = 1 $, | ||
| + | then for any positive linear functional $ f $ | ||
| + | on $ E $, | ||
| + | $ \| f \| = f ( 1) $ | ||
| + | and $ f ( x ^ {*} x ) \leq f ( 1) r ( x ^ {*} x ) $, | ||
| + | where $ r ( x ^ {*} x ) $ | ||
| + | is the [[Spectral radius|spectral radius]] of $ x ^ {*} x $( | ||
| + | see [[Banach algebra|Banach algebra]]). | ||
| − | A Hermitian element of a total involution algebra has a real spectrum. For any maximal closed left ideal | + | A Hermitian element of a total involution algebra has a real spectrum. For any maximal closed left ideal $ I $ |
| + | in a total involution algebra $ E $ | ||
| + | with a unit there is a positive linear functional on $ f $ | ||
| + | on $ E $ | ||
| + | such that $ I = \{ {x \in E } : {f ( x ^ {*} x ) = 0 } \} $. | ||
| + | An element $ x $ | ||
| + | in a total involution algebra $ E $ | ||
| + | is left-invertible in $ E $ | ||
| + | if and only if $ f ( x ^ {*} x ) > 0 $ | ||
| + | for all non-zero positive functionals $ f $ | ||
| + | on $ E $. | ||
| + | The radical of a total involution algebra $ E $ | ||
| + | coincides with the set of elements $ x \in E $ | ||
| + | such that $ f ( x ^ {*} x ) = 0 $ | ||
| + | for all positive linear functionals $ f $ | ||
| + | on $ E $. | ||
| + | A Banach algebra with involution $ E $ | ||
| + | with a unit 1 is a total involution algebra if and only if $ r ( x ^ {*} x ) = \sup f ( x ^ {*} x ) $, | ||
| + | where the supremum is taken over the set of positive linear functionals $ f $ | ||
| + | on $ E $ | ||
| + | for which $ f ( 1) = 1 $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052520/i052520115.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V. Pták, "Banach algebras with involution" ''Manuscripta Math.'' , '''6''' : 3 (1972) pp. 245–290</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , '''2''' , Springer (1979)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052520/i052520115.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V. Pták, "Banach algebras with involution" ''Manuscripta Math.'' , '''6''' : 3 (1972) pp. 245–290</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , '''2''' , Springer (1979)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | A (Banach, normed) algebra with involution is also called an involutive (Banach, normed) algebra. If in an involutive Banach algebra | + | A (Banach, normed) algebra with involution is also called an involutive (Banach, normed) algebra. If in an involutive Banach algebra $ A $ |
| + | one has $ \| x x ^ {*} \| = \| x \| ^ {2} $ | ||
| + | for all $ x \in A $, | ||
| + | then $ A $ | ||
| + | is called a $ B ^ {*} $- | ||
| + | algebra. | ||
| − | Let | + | Let $ A $ |
| + | be a Banach algebra. A left-approximate identity in $ A $ | ||
| + | is a net $ \{ e _ {i} \} _ {i \in I } $ | ||
| + | of elements of $ A $( | ||
| + | cf. [[Net (directed set)|Net (directed set)]]) such that $ \lim\limits \| e _ {i} x - x \| = 0 $ | ||
| + | for all $ x \in A $. | ||
| + | A right-approximate identity is similarly defined, using $ \| x e _ {i} - x \| $. | ||
| + | A left- and right-approximate identity is simply called an approximate identity. Every $ B ^ {*} $- | ||
| + | algebra has an approximate identity. | ||
| − | An algebra with involution | + | An algebra with involution $ E $ |
| + | is also termed a symmetric algebra, and a total involution algebra is also called a completely symmetric algebra. Correspondingly, a homomorphism of algebras with involution $ \phi : E \rightarrow F $ | ||
| + | is called a symmetric homomorphism if $ \phi ( x ^ {*} ) = \phi ( x ) ^ {*} $ | ||
| + | for all $ x \in E $. | ||
| + | Unfortunately, the term symmetric algebra is also sometimes used to mean a total involution algebra. | ||
| − | A symmetric ideal of | + | A symmetric ideal of $ E $ |
| + | is an ideal $ M $ | ||
| + | such that $ M ^ {*} = \{ {m ^ {*} } : {m \in M } \} = M $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Functional analysis" , McGraw-Hill (1979)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Functional analysis" , McGraw-Hill (1979)</TD></TR></table> | ||
Latest revision as of 22:13, 5 June 2020
algebra with involution
An algebra $ E $ over the field of complex numbers endowed with an involution $ x \mapsto x ^ {*} $, $ x \in E $. Some examples are: the algebra of continuous functions on a compact set, in which the involution sends any function to its complex conjugate; the algebra of bounded linear operators on a Hilbert space, in which the involution sends any operator to its adjoint; the group algebra of a locally compact group; and the algebra of measures on a locally compact group. The element $ x ^ {*} \in E $ is called the conjugate, or adjoint, of $ x $. An element $ x \in E $ is called self-adjoint, or Hermitian, if $ x ^ {*} = x $, and normal if $ x ^ {*} x = x x ^ {*} $. If $ E $ contains a unit element 1, then an element $ x \in E $ such that $ x ^ {*} x = x x ^ {*} = 1 $ is called unitary. The set $ E _ {h} $ of Hermitian elements of $ E $ is a real vector subspace of $ E $, and any $ x \in E $ can be uniquely written in the form $ x = x _ {1} + i x _ {2} $, where $ x _ {1} , x _ {2} \in E _ {h} $. In this case $ x \in E $ is normal if and only if $ x _ {1} $ and $ x _ {2} $ commute. Every element of the form $ x ^ {*} x $ is Hermitian, and so is the unit element. If $ x $ is invertible, then so is $ x ^ {*} $, and $ ( x ^ {*} ) ^ {-} 1 = ( x ^ {-} 1 ) ^ {*} $. The spectrum of any Hermitian element (cf. Spectrum of an element) is symmetric about the real axis. An involution algebra $ E $ is called a total involution algebra if the spectrum of any element of the form $ x ^ {*} x $, $ x \in E $, is contained in the set of non-negative real numbers. Examples of total involution algebras are: the involution algebra of continuous functions on a compact set; the involution algebra of bounded linear operators on a Hilbert space; and group algebras of compact and commutative locally compact groups. The group algebras of non-compact semi-simple Lie groups are not total involution algebras. A commutative involution algebra $ E $ is a total involution algebra if and only if all its maximal ideals are symmetric, or if and only if all characters of $ E $ are Hermitian. Every $ C ^ {*} $- algebra is a total involution algebra.
A subset $ M $ of an involution algebra $ E $ is called an involution set if $ x ^ {*} \in M $ for all $ x \in M $. A mapping $ \phi : E \rightarrow F $ of involution algebras is called an involution mapping if $ \phi ( x) ^ {*} = \phi ( x ^ {*} ) $ for all $ x \in E $. The kernel of an involution homomorphism of involution algebras is a symmetric two-sided ideal. Every symmetric one-sided ideal is two-sided and the quotient algebra of an involution algebra by a symmetric ideal admits the structure of an involution algebra in a natural way. The radical (cf. Radical of rings and algebras) of an involution algebra is a symmetric ideal. An involution subalgebra $ F $ of an involution algebra $ E $ is an involution algebra. Let $ \widetilde{E} $ be the direct sum of an involution algebra $ E $ and the field $ \mathbf C $, in which the linear operations and the involution are defined componentwise and the multiplication is given by
$$ \{ x , \lambda \} \{ y , \mu \} = \ \{ x y + \lambda y + \mu x , \lambda \mu \} $$
for all $ \lambda , \mu \in \mathbf C $, $ x , y \in E $. Then $ \widetilde{E} $ is an involution algebra with a unit element.
A linear functional $ f $ on an involution algebra is called Hermitian if $ f ( x ^ {*} ) = \overline{ {f ( x) }}\; $ for all $ x \in E $, and positive if $ f ( x ^ {*} x ) \geq 0 $ for all $ x \in E $. The set $ E _ {h} ^ \prime $ of Hermitian linear functionals on $ E $ is a real vector subspace of $ E ^ \prime $, the dual of $ E $, and $ E ^ \prime $ is the direct sum of the subspaces $ E _ {h} ^ \prime $ and $ i E _ {h} ^ \prime $. If $ E $ has a unit 1, then every positive functional $ f $ on $ E $ is Hermitian and $ | f ( x) | ^ {2} \leq f ( 1) f ( x ^ {*} x ) $ for all $ x \in E $. If $ f $ is a positive functional on an involution algebra $ E $, then $ f ( y ^ {*} x ) = f ( x ^ {*} y ) $ and $ | f ( y ^ {*} x ) | ^ {2} \leq f ( y ^ {*} y) f( x ^ {*} x ) $ for all $ x , y \in E $.
Let $ E $ be an involution algebra equipped with a norm making $ E $ into a normed algebra and satisfying the condition $ \| x ^ {*} \| = \| x \| $ for all $ x \in E $. Then $ E $ is called a normed algebra with involution. If $ E $ is complete with respect to this norm, then $ E $ is called a Banach algebra with involution. Every normed algebra with involution $ E $ can be imbedded in a Banach algebra with involution $ \overline{E}\; $ containing $ E $ as a dense involution subalgebra. $ \overline{E}\; $ is uniquely defined up to an isometric involution isomorphism. $ \overline{E}\; $ is called the completion of $ E $. If $ E $ is a Banach algebra with involution having an approximate identity, then every positive linear functional $ f $ on $ E $ is continuous and can be extended to a positive linear functional on $ \overline{E}\; $. If $ E $ has a unit 1 and $ \| 1 \| = 1 $, then for any positive linear functional $ f $ on $ E $, $ \| f \| = f ( 1) $ and $ f ( x ^ {*} x ) \leq f ( 1) r ( x ^ {*} x ) $, where $ r ( x ^ {*} x ) $ is the spectral radius of $ x ^ {*} x $( see Banach algebra).
A Hermitian element of a total involution algebra has a real spectrum. For any maximal closed left ideal $ I $ in a total involution algebra $ E $ with a unit there is a positive linear functional on $ f $ on $ E $ such that $ I = \{ {x \in E } : {f ( x ^ {*} x ) = 0 } \} $. An element $ x $ in a total involution algebra $ E $ is left-invertible in $ E $ if and only if $ f ( x ^ {*} x ) > 0 $ for all non-zero positive functionals $ f $ on $ E $. The radical of a total involution algebra $ E $ coincides with the set of elements $ x \in E $ such that $ f ( x ^ {*} x ) = 0 $ for all positive linear functionals $ f $ on $ E $. A Banach algebra with involution $ E $ with a unit 1 is a total involution algebra if and only if $ r ( x ^ {*} x ) = \sup f ( x ^ {*} x ) $, where the supremum is taken over the set of positive linear functionals $ f $ on $ E $ for which $ f ( 1) = 1 $.
References
| [1] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [2] | J. Dixmier, "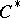 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
| [3] | V. Pták, "Banach algebras with involution" Manuscripta Math. , 6 : 3 (1972) pp. 245–290 |
| [4] | E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 2 , Springer (1979) |
Comments
A (Banach, normed) algebra with involution is also called an involutive (Banach, normed) algebra. If in an involutive Banach algebra $ A $ one has $ \| x x ^ {*} \| = \| x \| ^ {2} $ for all $ x \in A $, then $ A $ is called a $ B ^ {*} $- algebra.
Let $ A $ be a Banach algebra. A left-approximate identity in $ A $ is a net $ \{ e _ {i} \} _ {i \in I } $ of elements of $ A $( cf. Net (directed set)) such that $ \lim\limits \| e _ {i} x - x \| = 0 $ for all $ x \in A $. A right-approximate identity is similarly defined, using $ \| x e _ {i} - x \| $. A left- and right-approximate identity is simply called an approximate identity. Every $ B ^ {*} $- algebra has an approximate identity.
An algebra with involution $ E $ is also termed a symmetric algebra, and a total involution algebra is also called a completely symmetric algebra. Correspondingly, a homomorphism of algebras with involution $ \phi : E \rightarrow F $ is called a symmetric homomorphism if $ \phi ( x ^ {*} ) = \phi ( x ) ^ {*} $ for all $ x \in E $. Unfortunately, the term symmetric algebra is also sometimes used to mean a total involution algebra.
A symmetric ideal of $ E $ is an ideal $ M $ such that $ M ^ {*} = \{ {m ^ {*} } : {m \in M } \} = M $.
References
| [a1] | W. Rudin, "Functional analysis" , McGraw-Hill (1979) |
Involution algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Involution_algebra&oldid=18429