Difference between revisions of "Weyl quantization"
(Importing text file) |
(latex details) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 284 formulas, 257 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | Let $a ( x , \xi )$ be a classical Hamiltonian (cf. also [[Hamilton operator|Hamilton operator]]) defined on $\mathbf{R} ^ { n } \times \mathbf{R} ^ { n }$. The Weyl quantization rule associates to this function the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w1201103.png"/> defined on functions $u ( x )$ as | ||
| − | + | \begin{equation} \tag{a1} ( a ^ { w } u ) ( x ) = \end{equation} | |
| − | + | \begin{equation*} = \int \int e ^ { 2 i \pi ( x - y ) . \xi } a \left( \frac { x + y } { 2 } , \xi \right) u ( y ) d y d \xi. \end{equation*} | |
| − | + | For instance, $( x . \xi ) ^ { w } = ( x . D _ { x } + D _ { x } .x ) / 2$, with | |
| − | + | \begin{equation*} D _ { x } = \frac { 1 } { 2 i \pi } \frac { \partial } { \partial x }, \end{equation*} | |
| − | + | whereas the classical quantization rule would map the Hamiltonian $x \cdot \xi$ to the operator $x . D _ { x }$. A nice feature of the Weyl quantization rule, introduced in 1928 by H. Weyl [[#References|[a12]]], is the fact that real Hamiltonians get quantized by (formally) self-adjoint operators. Recall that the classical quantization of the Hamiltonian $a ( x , \xi )$ is given by the operator $\operatorname{Op} ( a )$ acting on functions $u ( x )$ by | |
| − | + | \begin{equation} \tag{a2} ( \operatorname{Op} ( a ) u ) ( x ) = \int e ^ { 2 i \pi x \cdot \xi } a ( x , \xi ) \hat { u } ( \xi ) d \xi, \end{equation} | |
| − | + | where the [[Fourier transform|Fourier transform]] $\widehat{u}$ is defined by | |
| − | + | \begin{equation} \tag{a3} \hat { u } ( \xi ) = \int e ^ { - 2 i \pi x . \xi } u ( x ) d x, \end{equation} | |
| − | + | so that $\check{\widehat { u }} = u$, with $\check{v} ( x ) = v ( - x )$. In fact, introducing the one-parameter group $J ^ { t } = \operatorname { exp } 2 i \pi t D _ { x } . D _ { \xi }$, given by the integral formula | |
| + | |||
| + | \begin{equation} \tag{a4} ( J ^ { t } a ) ( x , \xi ) = \end{equation} | ||
| + | |||
| + | \begin{equation*} = | t | ^ { - n } \int \int e ^ { - 2 i \pi t ^ { - 1 } y . \eta } { a ( x + y , \xi + \eta ) d y d \eta }, \end{equation*} | ||
one sees that | one sees that | ||
| − | + | \begin{equation*} ( \operatorname{Op} ( J ^ { t } a ) u ) ( x ) = \end{equation*} | |
| − | + | \begin{equation*} = \int \int e ^ { 2 i \pi ( x - y ) . \xi } a ( ( 1 - t ) x + t y , \xi ) u ( y ) d y d \xi. \end{equation*} | |
| − | In particular, one gets | + | In particular, one gets $a ^ { w } = \text{Op} ( J ^ { 1 / 2 } a )$. Moreover, since $( \operatorname{Op} ( a ) ) ^ { * } = \operatorname{Op} ( J \overline { a } )$ one obtains |
| − | + | \begin{equation*} ( a ^ { w } ) ^ { * } = \operatorname { Op } \left( J ( \overline { ( J ^ { 1 / 2 } a ) } \right) = \operatorname { Op } ( J ^ { 1 / 2 } \overline { a } ) = ( \overline { a } ) ^ { w }, \end{equation*} | |
| − | yielding formal self-adjointness for real | + | yielding formal self-adjointness for real $a$ (cf. also [[Self-adjoint operator|Self-adjoint operator]]). |
==Wigner functions.== | ==Wigner functions.== | ||
Formula (a1) can be written as | Formula (a1) can be written as | ||
| − | + | \begin{equation} \tag{a5} ( a ^ { w } u , v ) = \int \int a ( x , \xi ) {\cal H} ( u , v ) ( x , \xi ) d x d \xi, \end{equation} | |
| − | where the Wigner function | + | where the Wigner function $\mathcal{H}$ is defined as |
| − | + | \begin{equation} \tag{a6} \mathcal{H} ( u , v ) ( x , \xi ) = \end{equation} | |
| − | + | \begin{equation*} = \int u \left( x + \frac { y } { 2 } \right) \overline{v} \left( x - \frac { y } { 2 } \right) e ^ { - 2 i \pi y \cdot \xi } d y. \end{equation*} | |
| − | The mapping | + | The mapping $( u , v ) \mapsto \mathcal{H} ( u , v )$ is sesquilinear continuous from $\mathcal{S} ( \mathbf{R} ^ { n } ) \times \mathcal{S} ( \mathbf{R} ^ { n } )$ to $\mathcal{S} ( \mathbf{R} ^ { 2 n } )$, so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w12011035.png"/> makes sense for $a \in {\cal S} ^ { \prime } ( {\bf R} ^ { 2 n } )$ (here, $u , v \in \mathcal{S} ( \mathbf{R} ^ { n } )$ and $\mathcal{S} ^ { * }$ stands for the anti-dual): |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w12011039.png"/></td> </tr></table> |
The Wigner function also satisfies | The Wigner function also satisfies | ||
| − | + | \begin{equation*} \| \mathcal{H} ( u , v ) \| _ { L ^ { 2 } ( \mathbf{R} ^{n}) } = \| u \|_ { L ^ { 2 } ( \mathbf{R} ^{n}) } \| v \| _ { L ^ { 2 } ( \mathbf{R} ^{n}) } , \end{equation*} | |
| − | + | \begin{equation*} \mathcal{H} ( u , v ) ( x , \xi ) = 2 ^ { n } \langle \sigma _ { x , \xi }u , v \rangle _ { L^2 ( \mathbf{R} ^ { n } )} , ( \sigma _ { x , \xi} u ) ( y ) = u ( 2 x - y ) \operatorname { exp } ( - 4 i \pi ( x - y ) . \xi). \end{equation*} | |
| − | and the phase symmetries | + | and the phase symmetries $\sigma _{X}$ are unitary and self-adjoint operators on $L ^ { 2 } ( \mathbf{R} ^ { n } )$. Also ([[#References|[a10]]], [[#References|[a12]]]), |
| − | + | \begin{equation*} \alpha ^ { w } = \int _ { \mathbf{R} ^ { 2 n } } a ( X ) 2 ^ { n } \sigma _ { X } d X = \end{equation*} | |
| − | + | \begin{equation*} = \int _ { \mathbf{R} ^ { 2 n } } \hat { a } ( \Xi ) \operatorname { exp } ( 2 i \pi \Xi . M ) d \Xi \end{equation*} | |
| − | where | + | where $\Xi \cdot M = \hat{x} \cdot x + \widehat { \xi } \cdot D _{x}$ (here $ \Xi = ( \hat { x } , \hat { \xi } )$). These formulas give, in particular, |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w12011048.png"/></td> </tr></table> |
| − | where | + | where $\mathcal{L} ( L ^ { 2 } )$ stands for the space of bounded linear mappings from $L ^ { 2 } ( \mathbf{R} ^ { n } )$ into itself. The operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w12011051.png"/> is in the Hilbert–Schmidt class (cf. also [[Hilbert–Schmidt operator|Hilbert–Schmidt operator]]) if and only if $a$ belongs to $L ^ { 2 } ( \mathbf{R} ^ { 2 n } )$ and $\| a\| _{\text{HS}} = \| a \| _ { L } 2 _ { ( \mathbf{R} ^ { 2 n }) } $. To get this, it suffices to notice the relationship between the symbol $a$ of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w12011056.png"/> and its distribution kernel $k$: |
| − | + | \begin{equation*} a ( x , \xi ) = \int k \left( x + \frac { t } { 2 } , x - \frac { t } { 2 } \right) e ^ { - 2 i \pi t \xi } d t. \end{equation*} | |
The Fourier transform of the Wigner function is the so-called ambiguity function | The Fourier transform of the Wigner function is the so-called ambiguity function | ||
| − | + | \begin{equation} \tag{a7} {\cal A} ( u , v ) ( \xi , x ) = \int u \left( z - \frac { x } { 2 } \right) \bar{v} \left( z + \frac { x } { 2 } \right) e ^ { - 2 i \pi z . \xi } d z. \end{equation} | |
| − | For | + | For $\varphi , \psi \in L ^ { 2 } ( \mathbf{R} ^ { n} )$, the Wigner function $\mathcal{H} ( \varphi , \psi )$ is the Weyl symbol of the operator $u \mapsto ( u , \psi ) \varphi$ (cf. also [[Symbol of an operator|Symbol of an operator]]), where $( u , \psi )$ is the $L^{2}$ (Hermitian) dot-product, so that from (a5) one finds |
| − | + | \begin{equation*} (u, \psi ) _ { L ^ { 2 } ( {\bf R} ^ { n } ) } ( \varphi , u ) _ { L ^ { 2 } ( {\bf R} ^ { n } ) } = ( {\cal H} ( u , v ) , {\cal H} ( \psi , \varphi ) ) _ { L ^ { 2 } ( {\bf R} ^ { 2 n } ) }. \end{equation*} | |
As is shown below, the symplectic invariance of the Weyl quantization is actually its most important property. | As is shown below, the symplectic invariance of the Weyl quantization is actually its most important property. | ||
==Symplectic invariance.== | ==Symplectic invariance.== | ||
| − | Consider a finite-dimensional real [[Vector space|vector space]] | + | Consider a finite-dimensional real [[Vector space|vector space]] $E$ (the configuration space ${\bf R} _ { x } ^ { n }$) and its dual space $E ^ { * }$ (the momentum space ${\bf R} _ { \xi } ^ { n }$). The phase space is defined as $\Phi = E \oplus E ^ { * }$; its running point will be denoted, in general, by a capital letter ($X = ( x , \xi ) , Y = ( y , \eta )$). The symplectic form (cf. also [[Symplectic connection|Symplectic connection]]) on $\Phi$ is given by |
| − | + | \begin{equation} \tag{a8} [ ( x , \xi ) , ( y , \eta ) ] = \langle \xi , y \rangle _ { E ^{ * } , E } - \langle \eta , x \rangle _ { E ^{ * } , E }, \end{equation} | |
| − | where | + | where $\langle \cdot , \cdot \rangle _ { E ^ { * } , E}$ stands for the bracket of duality. The [[Symplectic group|symplectic group]] is the subgroup of the linear group of $\Phi$ preserving (a8). With |
| − | + | \begin{equation*} \sigma = \left( \begin{array} { c c } { 0 } & { \operatorname{Id} ( E ^ { * } ) } \\ { - \operatorname{Id} ( E ) } & { 0 } \end{array} \right), \end{equation*} | |
| − | for | + | for $X , Y \in \Phi$ one has |
| − | + | \begin{equation*} [ X , Y ] = \langle \sigma X , Y \rangle _ { \Phi ^ { * } , \Phi }, \end{equation*} | |
so that the equation of the symplectic group is | so that the equation of the symplectic group is | ||
| − | + | \begin{equation*} A ^ { * } \sigma A = \sigma. \end{equation*} | |
| − | One can describe a set of generators for the symplectic group | + | One can describe a set of generators for the symplectic group $\operatorname{Sp} ( n )$, identifying $\Phi$ with $\mathbf{R} _ { x } ^ { n } \times \mathbf{R} _ { \xi } ^ { n }$: the mappings |
| − | i) | + | i) $( x , \xi ) \mapsto ( T x , \square ^ { t } T ^ { - 1 } \xi )$, where $T$ is an automorphism of $E$; |
| − | ii) | + | ii) $( x _ { k } , \xi _ { k } ) \mapsto ( \xi _ { k } , - x _ { k } )$ and the other coordinates fixed; |
| − | iii) | + | iii) $( x , \xi ) \mapsto ( x , \xi + S x )$, where $S$ is symmetric from $E$ to $E ^ { * }$. One then describes the metaplectic group, introduced by A. Weil [[#References|[a11]]]. The metaplectic group $\operatorname{ Mp } ( n )$ is the subgroup of the group of unitary transformations of $L ^ { 2 } ( \mathbf{R} ^ { n } )$ generated by |
| − | j) | + | j) $( M _ { T } u ) ( x ) = | \operatorname { det } T \rceil ^ { - 1 / 2 } u ( T ^ { - 1 } x )$, where $T \in \operatorname{GL} ( n , \mathbf{R} )$; |
jj) partial Fourier transformations; | jj) partial Fourier transformations; | ||
| − | jjj) multiplication by | + | jjj) multiplication by $\operatorname { exp } ( i \pi \langle S x , x \rangle )$, where $S$ is a symmetric matrix. There exists a two-fold covering (the $\pi_{1}$ of both $\operatorname{ Mp } ( n )$ and $\operatorname{Sp} ( n )$ is $\bf Z$) |
| − | + | \begin{equation*} \pi : \operatorname { Mp} ( n ) \rightarrow \operatorname { Sp} ( n ) \end{equation*} | |
| − | such that, if | + | such that, if $\chi = \pi ( M )$ and $u$, $v$ are in $L ^ { 2 } ( \mathbf{R} ^ { n } )$, while $\mathcal{H} ( u , v )$ is their Wigner function, then |
| − | + | \begin{equation*} \mathcal{H} ( M u , M v ) = \mathcal{H} ( u , v ) \circ \chi ^ { - 1 }. \end{equation*} | |
| − | This is Segal's formula [[#References|[a9]]], which can be rephrased as follows. Let | + | This is Segal's formula [[#References|[a9]]], which can be rephrased as follows. Let $a \in {\cal S} ^ { \prime } ( {\bf R} ^ { 2 n } )$ and $\chi \in \operatorname { Sp } ( n )$. There exists an $M$ in the fibre of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110111.png"/> such that |
| − | + | \begin{equation} \tag{a9} ( a \circ \chi ) ^ { w } = M ^ { * } a ^ { w } M. \end{equation} | |
| − | In particular, the images by | + | In particular, the images by $\pi$ of the transformations j), jj), jjj) are, respectively, i), ii), iii). Moreover, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110114.png"/> is the phase translation, $\chi ( x , \xi ) = ( x + x _ { 0 } , \xi + \xi _ { 0 } )$, (a9) is fulfilled with $M = \tau _ { x _ { 0 } , \xi _ { 0 }}$ and phase translation given by |
| − | + | \begin{equation*} ( \tau _ { x _ { 0 } , \xi _ { 0 } } u ) ( y ) = u ( y - x _ { 0 } ) e ^ { 2 i \pi \langle y - x _ { 0 } / 2 , \xi _ { 0 } \rangle }. \end{equation*} | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110118.png" /> is the symmetry with respect to | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110118.png"/> is the symmetry with respect to $( x _ { 0 } , \xi _ { 0 } )$, $M$ in (a9) is, up to a unit factor, the phase symmetry $\sigma _ { x _ { 0 } , \xi _ { 0 } }$ defined above. This yields the following composition formula: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110122.png"/> with |
| − | + | \begin{equation} \tag{a10} ( a \sharp b ) ( X ) = \end{equation} | |
| − | + | \begin{equation*} = 2 ^ { 2 n } \int \int e ^ { - 4 i \pi [ X - Y , X - Z ] } { a } ( Y ) b ( Z ) d Y d Z , \end{equation*} | |
| − | with an integral on | + | with an integral on $\mathbf{R} ^ { 2 n } \times \mathbf{R} ^ { 2 n }$. One can compare this with the classical composition formula, |
| − | + | \begin{equation*} \operatorname {Op} ( a ) \operatorname {Op} ( b ) = \operatorname {Op} ( a \circ b ) \end{equation*} | |
(cf. (a2)) with | (cf. (a2)) with | ||
| − | + | \begin{equation*} ( a \circ b ) ( x , \xi ) = \int \int e ^ { - 2 i \pi y . \eta } a ( x , \xi + \eta ) b ( y + x , \xi ) d y d \eta, \end{equation*} | |
| − | with an integral on | + | with an integral on $\mathbf{R} ^ { n } \times \mathbf{R} ^ { n }$. It is convenient to give an asymptotic version of these compositions formulas, e.g. in the semi-classical case. Let $m$ be a real number. A smooth function $a ( x , \xi , h )$ defined on $\mathbf{R} _ { x } ^ { n } \times \mathbf{R} _ { \xi } ^ { n } \times ( 0,1 ]$ is in the symbol class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110133.png"/> if |
| − | < | + | \begin{equation*} \operatorname { sup } _ {\substack{ ( x , \xi ) \in {\bf R} ^ { 2 n }}, \\{0<h\leq 1} } \left| D _ { x } ^ { \alpha } D _ { \xi } ^ { \beta } a ( x , \xi , h ) \right| h ^ { m - | \beta | } < \infty . \end{equation*} |
| − | Then one has for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110135.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110136.png" /> the expansion | + | Then one has for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110135.png"/> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110136.png"/> the expansion |
| − | + | \begin{equation} \tag{a11} ( a \sharp b ) ( x , \xi ) = r _ { N } ( a , b ) + \end{equation} | |
| − | < | + | \begin{equation*} + \sum _ { 0 \leq k < N } 2 ^ { - k } \sum _ { | \alpha | + | \beta | = k } \frac { ( - 1 ) ^ { | \beta | } } { \alpha ! \beta ! } D _ { \xi } ^ { \alpha } \partial _ { x } ^ { \beta } a D _ { \xi } ^ { \beta } \partial _ { x } ^ { \alpha } b, \end{equation*} |
| − | with | + | with $r _ { N } ( a , b ) \in S _ { \text{scl} } ^ { m _ { 1 } + m _ { 2 } - N}$. The beginning of this expansion is thus |
| − | + | \begin{equation*} a b + \frac { 1 } { 2 \iota} \{ a , b \}, \end{equation*} | |
| − | where | + | where $\{ a , b \}$ denotes the [[Poisson brackets|Poisson brackets]] and $\iota = 2 \pi {i} $. The sums inside (a11) with $k$ even are symmetric in $a , b$ and skew-symmetric for $k$ odd. This can be compared to the classical expansion formula |
| − | + | \begin{equation*} ( a \circ b ) ( x , \xi ) = \sum _ { | \alpha | < N } \frac { 1 } { \alpha ! } D _ { \xi } ^ { \alpha } a \partial _ { x } ^ { \alpha } b + t _ { N } ( a , b ), \end{equation*} | |
| − | with | + | with $t _ { N } ( a , b ) \in S _ { \text{scl} } ^ { m _ { 1 } + m _ { 2 } - N }$. Moreover, for $a _ { 1 } , \dots , a _ { 2k } $ in $L ^ { 1 } ( \Phi = \mathbf{R} ^ { 2 n } )$, the multiple composition formula gives |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110150.png"/></td> </tr></table> |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110151.png"/></td> </tr></table> |
| − | + | \begin{equation*} .d Y _ { 1 } \ldots d Y _ { 2 k }, \end{equation*} | |
| − | and if | + | and if $a _ { 2 k + 1 } \in L ^ { 1 } ( \Phi )$, |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110154.png"/></td> </tr></table> |
| − | + | \begin{equation*} = 2 ^ { 2 n k } \int _ { \Phi ^ { 2 k } } a _ { 1 } ( Y _ { 1 } ) \ldots a _ { 2 k } ( Y _ { 2 k } ) \text{..} a _ { 2 k + 1 } \left( X + \sum _ { 1 \leq j < l \leq 2 k } ( - 1 ) ^ { j + l } ( Y _ { j } - Y _ { l } ) \right). \end{equation*} | |
| − | < | + | \begin{equation*} .\operatorname { exp } 4 i \pi \sum _ { 1 \leq j < l \leq 2 k } ( - 1 ) ^ { j + l } [ X - Y _ { j } , X - Y _ { l } ] .. d Y _ { 1 } \ldots d Y _ { 2 k }. \end{equation*} |
| − | Consider the standard sum of homogeneous symbols defined on | + | Consider the standard sum of homogeneous symbols defined on $\Omega \times \mathbf{R} ^ { n }$, where $\Omega$ is an open subset of ${\bf R} ^ { n }$, |
| − | + | \begin{equation*} a = a _ { m } + a _ { m - 1 } + r _ { m - 2 }, \end{equation*} | |
| − | with | + | with $a _ { j }$ smooth on $\Omega \times \mathbf{R} ^ { n }$ and homogeneous in the following sense: |
| − | + | \begin{equation*} a _ { j } ( x , \lambda \xi ) = \lambda ^ { j } a _ { j } ( x , \xi ) , \text { for } | \xi | \geq 1 , \lambda \geq 1, \end{equation*} | |
| − | and | + | and $r _ { m - 2} \in S _ { \text{loc} } ^ { m - 2 } ( \Omega )$, i.e. for all compact subsets $K$ of $\Omega$, |
| − | + | \begin{equation*} \operatorname { sup } _ { x \in K, \atop \xi \in {\bf R} ^ { n } } \left| ( D _ { x } ^ { \alpha } D _ { \xi } ^ { \beta } r _ { m - 2 } ) ( x , \xi ) \right| ( 1 + | \xi | ) ^ { 2 - m + | \beta | } < \infty. \end{equation*} | |
| − | This class of pseudo-differential operators (cf. also [[Pseudo-differential operator|Pseudo-differential operator]]) is invariant under diffeomorphisms, and using the Weyl quantization one gets that the principal symbol | + | This class of pseudo-differential operators (cf. also [[Pseudo-differential operator|Pseudo-differential operator]]) is invariant under diffeomorphisms, and using the Weyl quantization one gets that the principal symbol $a _ { m }$ is invariantly defined on the cotangent bundle $T ^ { * } ( \Omega )$ whereas the subprincipal symbol $a_{m - 1}$ is invariantly defined on the double characteristic set |
| − | + | \begin{equation*} \{ a _ { m } = 0 , d a _ { m } = 0 \} \end{equation*} | |
of the principal symbol. If one writes | of the principal symbol. If one writes | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110172.png"/></td> </tr></table> |
| − | one gets | + | one gets $a = J ^ { - 1 / 2 } b$ and $a _ { m } = b _ { m }$. Moreover, |
| − | + | \begin{equation*} a _ { m - 1 } = b _ { m - 1 } - \frac { 1 } { 2 \iota } \sum _ { 1 \leq j \leq n } \frac { \partial ^ { 2 } b _ { m } } { \partial x _ { j } \partial \xi _ { j } } = b _ { m - 1 } ^ { s }. \end{equation*} | |
| − | Thus, if one defines the subprincipal symbol as the above analytic expression | + | Thus, if one defines the subprincipal symbol as the above analytic expression $b ^ { s } _{m - 1}$ where $b = b _ { m } + b _ { m - 1} + \ldots$ is the classical symbol of $a ^ { w } = \operatorname{Op} ( b )$, one finds that this invariant $b ^ { s } _{m - 1}$ is simply the second term $a_{m - 1}$ in the expansion of the Weyl symbol $a$. In the same vein, it is also useful to note that when considering pseudo-differential operators acting on half-densities one gets a refined principal symbol $a _ { m } + a _ { m - 1 }$ invariant by diffeomorphism. |
==Weyl–Hörmander calculus and admissible metrics.== | ==Weyl–Hörmander calculus and admissible metrics.== | ||
| − | The developments of the analysis of partial differential operators in the 1970s required refined localizations in the phase space. E.g., the Beals–Fefferman local solvability theorem [[#References|[a2]]] yields the geometric condition (P) as an if-and-only-if solvability condition for differential operators of principal type (with possibly complex symbols). These authors removed the analyticity assumption used by L. Nirenberg and F. Treves, and a key point in their method is a Calderón–Zygmund decomposition of the symbol, that is, a micro-localization procedure depending on a particular function, yielding a pseudo-differential calculus tailored to the symbol under investigation. Another example is provided by the Fefferman–Phong inequality [[#References|[a6]]], establishing that second-order operators with non-negative symbols are bounded from below on | + | The developments of the analysis of partial differential operators in the 1970s required refined localizations in the phase space. E.g., the Beals–Fefferman local solvability theorem [[#References|[a2]]] yields the geometric condition (P) as an if-and-only-if solvability condition for differential operators of principal type (with possibly complex symbols). These authors removed the analyticity assumption used by L. Nirenberg and F. Treves, and a key point in their method is a Calderón–Zygmund decomposition of the symbol, that is, a micro-localization procedure depending on a particular function, yielding a pseudo-differential calculus tailored to the symbol under investigation. Another example is provided by the Fefferman–Phong inequality [[#References|[a6]]], establishing that second-order operators with non-negative symbols are bounded from below on $L^{2}$; a Calderón–Zygmund decomposition is needed in the proof, as well as an induction on the number of variables. These micro-localizations go much beyond the standard homogeneous calculus and also beyond the classes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110184.png"/>, previously called exotic. In 1979, L.V. Hörmander published [[#References|[a7]]], providing simple and general rules for a pseudo-differential calculus to be admissible. Consider a positive-definite quadratic form $G$ defined on $\Phi$. The dual quadratic form $G ^ { \sigma }$ with respect to the symplectic structure is |
| − | + | \begin{equation} \tag{a12} G ^ { \sigma } ( T ) = \operatorname { sup } _ { G ( U ) = 1 } [ T , U ] ^ { 2 } . \end{equation} | |
| − | Define an admissible metric on the phase space as a mapping from | + | Define an admissible metric on the phase space as a mapping from $\Phi$ to the set of positive-definite quadratic forms on $\Phi$, $X \mapsto G _ { X }$, such that the following three properties are fulfilled: |
| − | (uncertainty principle) For all | + | (uncertainty principle) For all $X \in \Phi$, |
| − | + | \begin{equation} \tag{a13} G _ { X } \leq G _ { X } ^ { g }; \end{equation} | |
| − | there exist some positive constants | + | there exist some positive constants $\rho$, $C$, such that, for all $X , Y \in \Phi$, |
| − | + | \begin{equation} \tag{a14} G _ { X } ( X - Y) \leq \rho ^ { 2 } \Rightarrow G _ { Y } \leq C G _ { X }; \end{equation} | |
| − | there exist some positive constants | + | there exist some positive constants $N$, $C$, such that, for all $X , Y \in \Phi$, |
| − | + | \begin{equation} \tag{a15} G _ { X } \leq C ( 1 + G _ { X } ^ { \sigma } ( X - Y ) ) ^ { N } G _ { Y }. \end{equation} | |
| − | Property (a13) is clearly related to the uncertainty principle, since for each | + | Property (a13) is clearly related to the uncertainty principle, since for each $X$ one can diagonalize the quadratic form $G _ { X }$ in a symplectic basis so that |
| − | + | \begin{equation*} G _ { X } = \sum _ { 1 \leq j \leq n } h _ { j } ( | d q _ { j } | ^ { 2 } + | d p _ { j } | ^ { 2 } ), \end{equation*} | |
| − | where | + | where $( q_j , p _ { j } )$ is a set of symplectic coordinates. One then gets |
| − | + | \begin{equation*} G _ { X } ^ { g } = \sum _ { 1 \leq j \leq n } h _ { j } ^ { - 1 } ( | d q _ { j } | ^ { 2 } + | d p _ { j } | ^ { 2 } ). \end{equation*} | |
| − | Condition (a13) thus means that | + | Condition (a13) thus means that $\operatorname{max} h_{j} \leq 1$, which can be rephrased in the familiarly vague version as |
| − | + | \begin{equation*} \Delta p _ { j } \Delta q_j \sim h _ { j } ^ { - 1 } \geq 1 \end{equation*} | |
| − | in the | + | in the $G$-balls. This condition is relevant to any micro-localization procedure. When $G = G ^ { \sigma }$, one says that the quadratic form is symplectic. Property (a14) is called slowness of the metric and is usually easy to verify. Property (a15) is the temperance of the metric and is more of a technical character, although very important in handling non-local terms in the composition formula. In particular, this property is useful to verify the assumptions of Cotlar's lemma. Moreover, one defines a weight $m$ as a positive function on $\Phi$ such that there exist positive constants $C$, $N$ so that for all $X , Y \in \Phi$, |
| − | + | \begin{equation} \tag{a16} m ( X ) \leq C ( 1 + G _ { X } ^ { \sigma } ( X - Y ) ) ^ { N } m ( Y ), \end{equation} | |
and | and | ||
| − | + | \begin{equation} \tag{a17} G _ { X } ( X - Y ) \leq C ^ { - 1 } \Rightarrow C ^ { - 1 } \leq \frac { m ( X ) } { m ( Y ) } \leq C. \end{equation} | |
| − | Eventually, one defines the class of symbols | + | Eventually, one defines the class of symbols $S ( m , G )$ as the $C ^ { \infty }$-functions $a$ on the phase space such that |
| − | + | \begin{equation} \tag{a18} \operatorname { sup } _ { X \in \Phi } \| a ^ { ( k ) } ( X ) \| _ { G _ { X } } m ( X ) ^ { - 1 } < \infty. \end{equation} | |
It is, for instance, easily checked that | It is, for instance, easily checked that | ||
| − | + | \begin{equation*} S _ { \rho , \delta } ^ { \mu } = S \left( \langle \xi \rangle ^ { \mu } , \langle \xi \rangle ^ { 2 \delta } | d x | ^ { 2 } + \langle \xi \rangle ^ { - 2 \rho } | d \xi | ^ { 2 } \right), \end{equation*} | |
| − | with | + | with $\langle \xi \rangle = 1 + | \xi |$ and that this metric is an admissible metric when $0 \leq \delta \leq \rho \leq 1$, $\delta < 1$. The metric defining $S _ { 1,1 } ^ { 0 }$ satisfies (a13)–(a14) but fails to satisfy (a15). Indeed, there are counterexamples showing that for the classical and the Weyl quantization [[#References|[a4]]] there are symbols in $S _ { 1,1 } ^ { 0 }$ whose quantization is not $L^{2}$-bounded. In fact, one of the building block for the calculus of pseudo-differential operators is the $L^{2}$-boundedness of the Weyl quantization of symbols in $S ( 1 , G )$, where $G$ is an admissible metric. One defines the Planck function of the calculus as |
| − | + | \begin{equation} \tag{a19} H ( X ) = \operatorname { sup } _ { T \neq 0 } \sqrt { \frac { G _{X} ( T ) } { G _ { X } ^ { \sigma } ( T ) } } \end{equation} | |
| − | and notes that from (a13), | + | and notes that from (a13), $H ( X ) \leq 1$. One obtains the composition formula (a11) with $\alpha \in S ( m _ { 1 } , G )$, $b \in S ( m _ { 2 } , G )$ and $r _ { N } ( a , b ) \in S ( m _ { 1 } m _ { 2 } H ^ { N } , G )$. In particular, one obtains, with obvious notations, |
| − | + | \begin{equation*} a \sharp b \in S ( m _ { 1 } m _ { 2 } , G ), \end{equation*} | |
| − | + | \begin{equation*} a \sharp b = a b + S ( m _ { 1 } m _ { 2 } H , G ) ,\; a \sharp b = a b + \frac { 1 } { 2 \iota } \{ a , b \} + S ( m _ { 1 } m _ { 2 } H ^ { 2 } , G ), \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110240.png"/></td> </tr></table> |
| − | The Fefferman–Phong inequality has also a simple expression in this framework: Let | + | The Fefferman–Phong inequality has also a simple expression in this framework: Let $a$ be a non-negative symbol in $S ( H ^ { - 2 } , G )$, then the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120110/w120110243.png"/> is semi-bounded from below in $L ^ { 2 } ( \mathbf{R} ^ { n } )$. The proof uses a Calderón–Zygmund decomposition and in fact one shows that $a \in S ( h ^ { - 2 } , g )$, where $h$ is the Planck function related to the admissible metric $g$ defined by |
| − | + | \begin{equation*} g_{X} ( T ) = \frac { G _ { X } ( T ) } { H ( X ) [ 1 + a ( X ) + H ( X ) ^ { 2 } \| a ^ { \prime \prime } ( X ) \| ^ { 2 _{ G _ { X }}} ] ^ { 1 / 2 } }. \end{equation*} | |
| − | On the other hand, if | + | On the other hand, if $G$ is an admissible metric and $q _ { \alpha } \in S ( H ^ { - 1 } , G )$ uniformly with respect to a parameter $\alpha$, the following metric also satisfies (a13)–(a15): $\tilde { g } _ { X } = H ( X ) ^ { - 1 } \tilde { h } ( X ) G _ { X } ( T )$, with |
| − | + | \begin{equation*} \widetilde { h } ( X ) ^ { - 1 } = 1 + \operatorname { sup } _ { \alpha } | q _ { \alpha } ( X ) | + H ( X ) \operatorname { sup } _ { \alpha } \| q _ { \alpha } ^ { \prime } ( X ) \| _ { G _ { X } } ^ { 2 }. \end{equation*} | |
| − | One gets in this case that | + | One gets in this case that $q _ { \alpha } \in S ( \tilde { h } ^ { - 1 } , \tilde{g} )$ uniformly. A key point in the Beals–Fefferman proof of local solvability under condition (P) can be reformulated through the construction of the previous metric. Sobolev spaces related to this type of calculus were studied in [[#References|[a1]]] (cf. also [[Sobolev space|Sobolev space]]). For an admissible metric $G$ and a weight $m$, the space $H ( m , G )$ is defined as |
| − | + | \begin{equation*} \{ u \in \mathcal{S} ^ { \prime } ( \mathbf{R} ^ { n } ) : \forall a \in S ( m , G ) , a ^ { w } u \in L ^ { 2 } ( \mathbf{R} ^ { n } ) \}. \end{equation*} | |
| − | It can be proven that a Hilbertian structure can be set on | + | It can be proven that a Hilbertian structure can be set on $H ( m , G )$, that $H ( 1 , G ) = L ^ { 2 } ( \mathbf{R} ^ { n } )$ and that for $a \in S ( m , G )$ and $m_1$ another weight, the mapping |
| − | + | \begin{equation*} a ^ { w } : H ( m m _ { 1 } , G ) \rightarrow H ( m _ { 1 } , G ) \end{equation*} | |
is continuous. | is continuous. | ||
| Line 278: | Line 286: | ||
Further developments of the Weyl calculus were explored in [[#References|[a3]]], with higher-order micro-localizations. Several metrics | Further developments of the Weyl calculus were explored in [[#References|[a3]]], with higher-order micro-localizations. Several metrics | ||
| − | + | \begin{equation*} g _ { 1 } \leq \ldots \leq g _ { k } \end{equation*} | |
| − | are given on the phase space. All these metrics satisfy (a13)–(a14), but, except for | + | are given on the phase space. All these metrics satisfy (a13)–(a14), but, except for $g_1$, fail to satisfy globally the temperance condition (a15). Instead, the metric $g_{l+ 1}$ is assumed to be (uniformly) temperate on the $g_{l}$-balls. It is then possible to produce a satisfactory quantization formula for symbols belonging to a class $S ( m , g _ { k } )$. A typical example is given in [[#References|[a5]]], with applications to propagation of singularities for non-linear hyperbolic equations: |
| − | + | \begin{equation*} g _ { 1 } = | d x | ^ { 2 } + \frac { | d \xi | ^ { 2 } } { | \xi | ^ { 2 } } \leq g_2 = \frac { | d x | ^ { 2 } } { | x | ^ { 2 } } + \frac { | d \xi | ^ { 2 } } { | \xi | ^ { 2 } }, \end{equation*} | |
| − | where | + | where $g_1$ is defined on $| \xi | > 1$, and $g_{2}$ on |
| − | < | + | \begin{equation*} \{ | x | < 1 , | x | | \xi | > 1 \} \end{equation*} |
| − | It is then possible to quantize functions | + | It is then possible to quantize functions $a ( x , \xi )$ homogeneous of degree $\mu$ in the variable $x$, and $\nu$ in the variable $\xi $, so as to get composition formulas, Sobolev spaces, and the standard pseudo-differential apparatus allowing a commutator argument to work for propagation results. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J.-M. Bony, J.-Y. Chemin, "Espaces fonctionnels associés au calcul de Weyl–Hörmander" ''Bull. Soc. Math. France'' , '''122''' (1994) pp. 77–118 {{MR|}} {{ZBL|0798.35172}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> R. Beals, C. Fefferman, "On local solvability of linear partial differential equations" ''Ann. of Math.'' , '''97''' (1973) pp. 482–498 {{MR|0352746}} {{ZBL|0256.35002}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J.-M. Bony, N. Lerner, "Quantification asymtotique et microlocalisations d'ordre supérieur" ''Ann. Sci. Ecole Norm. Sup.'' , '''22''' (1989) pp. 377–483</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> A. Boulkhemair, "Remarque sur la quantification de Weyl pour la classe de symboles $S _ { 1,1 } ^ { 0 }$" ''C.R. Acad. Sci. Paris'' , '''321''' : 8 (1995) pp. 1017–1022 {{MR|1360564}} {{ZBL|0842.35144}} </td></tr><tr><td valign="top">[a5]</td> <td valign="top"> J.-M. Bony, "Second microlocalization and propagation of singularities for semi-linear hyperbolic equations" K. Mizohata (ed.) , ''Hyperbolic Equations and Related Topics'' , Kinokuniya (1986) pp. 11–49 {{MR|925240}} {{ZBL|}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> C. Fefferman, D.H. Phong, "On positivity of pseudo-differential operators" ''Proc. Nat. Acad. Sci. USA'' , '''75''' (1978) pp. 4673–4674 {{MR|0507931}} {{ZBL|0391.35062}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> L. Hörmander, "The Weyl calculus of pseudo-differential operators" ''Commun. Pure Appl. Math.'' , '''32''' (1979) pp. 359–443 {{MR|517939}} {{ZBL|0388.47032}} </td></tr><tr><td valign="top">[a8]</td> <td valign="top"> L. Hörmander, "The analysis of linear partial differential operators III-IV" , Springer (1985)</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> I. Segal, "Transforms for operators and asymptotic automorphisms over a locally compact abelian group" ''Math. Scand.'' , '''13''' (1963) pp. 31–43</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> A. Unterberger, "Oscillateur harmonique et opérateurs pseudo-différentiels" ''Ann. Inst. Fourier'' , '''29''' : 3 (1979) pp. 201–221 {{MR|0552965}} {{ZBL|0396.47027}} </td></tr><tr><td valign="top">[a11]</td> <td valign="top"> A. Weil, "Sur certains groupes d'opérateurs unitaires" ''Acta Math.'' , '''111''' (1964) pp. 143–211 {{MR|0165033}} {{ZBL|}} </td></tr><tr><td valign="top">[a12]</td> <td valign="top"> H. Weyl, "Gruppentheorie und Quantenmechanik" , S. Hirzel (1928) {{MR|0450450}} {{ZBL|54.0954.03}} </td></tr></table> |
Latest revision as of 19:54, 6 February 2024
Let $a ( x , \xi )$ be a classical Hamiltonian (cf. also Hamilton operator) defined on $\mathbf{R} ^ { n } \times \mathbf{R} ^ { n }$. The Weyl quantization rule associates to this function the operator  defined on functions $u ( x )$ as
defined on functions $u ( x )$ as
\begin{equation} \tag{a1} ( a ^ { w } u ) ( x ) = \end{equation}
\begin{equation*} = \int \int e ^ { 2 i \pi ( x - y ) . \xi } a \left( \frac { x + y } { 2 } , \xi \right) u ( y ) d y d \xi. \end{equation*}
For instance, $( x . \xi ) ^ { w } = ( x . D _ { x } + D _ { x } .x ) / 2$, with
\begin{equation*} D _ { x } = \frac { 1 } { 2 i \pi } \frac { \partial } { \partial x }, \end{equation*}
whereas the classical quantization rule would map the Hamiltonian $x \cdot \xi$ to the operator $x . D _ { x }$. A nice feature of the Weyl quantization rule, introduced in 1928 by H. Weyl [a12], is the fact that real Hamiltonians get quantized by (formally) self-adjoint operators. Recall that the classical quantization of the Hamiltonian $a ( x , \xi )$ is given by the operator $\operatorname{Op} ( a )$ acting on functions $u ( x )$ by
\begin{equation} \tag{a2} ( \operatorname{Op} ( a ) u ) ( x ) = \int e ^ { 2 i \pi x \cdot \xi } a ( x , \xi ) \hat { u } ( \xi ) d \xi, \end{equation}
where the Fourier transform $\widehat{u}$ is defined by
\begin{equation} \tag{a3} \hat { u } ( \xi ) = \int e ^ { - 2 i \pi x . \xi } u ( x ) d x, \end{equation}
so that $\check{\widehat { u }} = u$, with $\check{v} ( x ) = v ( - x )$. In fact, introducing the one-parameter group $J ^ { t } = \operatorname { exp } 2 i \pi t D _ { x } . D _ { \xi }$, given by the integral formula
\begin{equation} \tag{a4} ( J ^ { t } a ) ( x , \xi ) = \end{equation}
\begin{equation*} = | t | ^ { - n } \int \int e ^ { - 2 i \pi t ^ { - 1 } y . \eta } { a ( x + y , \xi + \eta ) d y d \eta }, \end{equation*}
one sees that
\begin{equation*} ( \operatorname{Op} ( J ^ { t } a ) u ) ( x ) = \end{equation*}
\begin{equation*} = \int \int e ^ { 2 i \pi ( x - y ) . \xi } a ( ( 1 - t ) x + t y , \xi ) u ( y ) d y d \xi. \end{equation*}
In particular, one gets $a ^ { w } = \text{Op} ( J ^ { 1 / 2 } a )$. Moreover, since $( \operatorname{Op} ( a ) ) ^ { * } = \operatorname{Op} ( J \overline { a } )$ one obtains
\begin{equation*} ( a ^ { w } ) ^ { * } = \operatorname { Op } \left( J ( \overline { ( J ^ { 1 / 2 } a ) } \right) = \operatorname { Op } ( J ^ { 1 / 2 } \overline { a } ) = ( \overline { a } ) ^ { w }, \end{equation*}
yielding formal self-adjointness for real $a$ (cf. also Self-adjoint operator).
Wigner functions.
Formula (a1) can be written as
\begin{equation} \tag{a5} ( a ^ { w } u , v ) = \int \int a ( x , \xi ) {\cal H} ( u , v ) ( x , \xi ) d x d \xi, \end{equation}
where the Wigner function $\mathcal{H}$ is defined as
\begin{equation} \tag{a6} \mathcal{H} ( u , v ) ( x , \xi ) = \end{equation}
\begin{equation*} = \int u \left( x + \frac { y } { 2 } \right) \overline{v} \left( x - \frac { y } { 2 } \right) e ^ { - 2 i \pi y \cdot \xi } d y. \end{equation*}
The mapping $( u , v ) \mapsto \mathcal{H} ( u , v )$ is sesquilinear continuous from $\mathcal{S} ( \mathbf{R} ^ { n } ) \times \mathcal{S} ( \mathbf{R} ^ { n } )$ to $\mathcal{S} ( \mathbf{R} ^ { 2 n } )$, so that 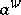 makes sense for $a \in {\cal S} ^ { \prime } ( {\bf R} ^ { 2 n } )$ (here, $u , v \in \mathcal{S} ( \mathbf{R} ^ { n } )$ and $\mathcal{S} ^ { * }$ stands for the anti-dual):
makes sense for $a \in {\cal S} ^ { \prime } ( {\bf R} ^ { 2 n } )$ (here, $u , v \in \mathcal{S} ( \mathbf{R} ^ { n } )$ and $\mathcal{S} ^ { * }$ stands for the anti-dual):
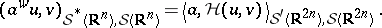 |
The Wigner function also satisfies
\begin{equation*} \| \mathcal{H} ( u , v ) \| _ { L ^ { 2 } ( \mathbf{R} ^{n}) } = \| u \|_ { L ^ { 2 } ( \mathbf{R} ^{n}) } \| v \| _ { L ^ { 2 } ( \mathbf{R} ^{n}) } , \end{equation*}
\begin{equation*} \mathcal{H} ( u , v ) ( x , \xi ) = 2 ^ { n } \langle \sigma _ { x , \xi }u , v \rangle _ { L^2 ( \mathbf{R} ^ { n } )} , ( \sigma _ { x , \xi} u ) ( y ) = u ( 2 x - y ) \operatorname { exp } ( - 4 i \pi ( x - y ) . \xi). \end{equation*}
and the phase symmetries $\sigma _{X}$ are unitary and self-adjoint operators on $L ^ { 2 } ( \mathbf{R} ^ { n } )$. Also ([a10], [a12]),
\begin{equation*} \alpha ^ { w } = \int _ { \mathbf{R} ^ { 2 n } } a ( X ) 2 ^ { n } \sigma _ { X } d X = \end{equation*}
\begin{equation*} = \int _ { \mathbf{R} ^ { 2 n } } \hat { a } ( \Xi ) \operatorname { exp } ( 2 i \pi \Xi . M ) d \Xi \end{equation*}
where $\Xi \cdot M = \hat{x} \cdot x + \widehat { \xi } \cdot D _{x}$ (here $ \Xi = ( \hat { x } , \hat { \xi } )$). These formulas give, in particular,
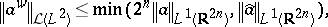 |
where $\mathcal{L} ( L ^ { 2 } )$ stands for the space of bounded linear mappings from $L ^ { 2 } ( \mathbf{R} ^ { n } )$ into itself. The operator 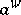 is in the Hilbert–Schmidt class (cf. also Hilbert–Schmidt operator) if and only if $a$ belongs to $L ^ { 2 } ( \mathbf{R} ^ { 2 n } )$ and $\| a\| _{\text{HS}} = \| a \| _ { L } 2 _ { ( \mathbf{R} ^ { 2 n }) } $. To get this, it suffices to notice the relationship between the symbol $a$ of
is in the Hilbert–Schmidt class (cf. also Hilbert–Schmidt operator) if and only if $a$ belongs to $L ^ { 2 } ( \mathbf{R} ^ { 2 n } )$ and $\| a\| _{\text{HS}} = \| a \| _ { L } 2 _ { ( \mathbf{R} ^ { 2 n }) } $. To get this, it suffices to notice the relationship between the symbol $a$ of  and its distribution kernel $k$:
and its distribution kernel $k$:
\begin{equation*} a ( x , \xi ) = \int k \left( x + \frac { t } { 2 } , x - \frac { t } { 2 } \right) e ^ { - 2 i \pi t \xi } d t. \end{equation*}
The Fourier transform of the Wigner function is the so-called ambiguity function
\begin{equation} \tag{a7} {\cal A} ( u , v ) ( \xi , x ) = \int u \left( z - \frac { x } { 2 } \right) \bar{v} \left( z + \frac { x } { 2 } \right) e ^ { - 2 i \pi z . \xi } d z. \end{equation}
For $\varphi , \psi \in L ^ { 2 } ( \mathbf{R} ^ { n} )$, the Wigner function $\mathcal{H} ( \varphi , \psi )$ is the Weyl symbol of the operator $u \mapsto ( u , \psi ) \varphi$ (cf. also Symbol of an operator), where $( u , \psi )$ is the $L^{2}$ (Hermitian) dot-product, so that from (a5) one finds
\begin{equation*} (u, \psi ) _ { L ^ { 2 } ( {\bf R} ^ { n } ) } ( \varphi , u ) _ { L ^ { 2 } ( {\bf R} ^ { n } ) } = ( {\cal H} ( u , v ) , {\cal H} ( \psi , \varphi ) ) _ { L ^ { 2 } ( {\bf R} ^ { 2 n } ) }. \end{equation*}
As is shown below, the symplectic invariance of the Weyl quantization is actually its most important property.
Symplectic invariance.
Consider a finite-dimensional real vector space $E$ (the configuration space ${\bf R} _ { x } ^ { n }$) and its dual space $E ^ { * }$ (the momentum space ${\bf R} _ { \xi } ^ { n }$). The phase space is defined as $\Phi = E \oplus E ^ { * }$; its running point will be denoted, in general, by a capital letter ($X = ( x , \xi ) , Y = ( y , \eta )$). The symplectic form (cf. also Symplectic connection) on $\Phi$ is given by
\begin{equation} \tag{a8} [ ( x , \xi ) , ( y , \eta ) ] = \langle \xi , y \rangle _ { E ^{ * } , E } - \langle \eta , x \rangle _ { E ^{ * } , E }, \end{equation}
where $\langle \cdot , \cdot \rangle _ { E ^ { * } , E}$ stands for the bracket of duality. The symplectic group is the subgroup of the linear group of $\Phi$ preserving (a8). With
\begin{equation*} \sigma = \left( \begin{array} { c c } { 0 } & { \operatorname{Id} ( E ^ { * } ) } \\ { - \operatorname{Id} ( E ) } & { 0 } \end{array} \right), \end{equation*}
for $X , Y \in \Phi$ one has
\begin{equation*} [ X , Y ] = \langle \sigma X , Y \rangle _ { \Phi ^ { * } , \Phi }, \end{equation*}
so that the equation of the symplectic group is
\begin{equation*} A ^ { * } \sigma A = \sigma. \end{equation*}
One can describe a set of generators for the symplectic group $\operatorname{Sp} ( n )$, identifying $\Phi$ with $\mathbf{R} _ { x } ^ { n } \times \mathbf{R} _ { \xi } ^ { n }$: the mappings
i) $( x , \xi ) \mapsto ( T x , \square ^ { t } T ^ { - 1 } \xi )$, where $T$ is an automorphism of $E$;
ii) $( x _ { k } , \xi _ { k } ) \mapsto ( \xi _ { k } , - x _ { k } )$ and the other coordinates fixed;
iii) $( x , \xi ) \mapsto ( x , \xi + S x )$, where $S$ is symmetric from $E$ to $E ^ { * }$. One then describes the metaplectic group, introduced by A. Weil [a11]. The metaplectic group $\operatorname{ Mp } ( n )$ is the subgroup of the group of unitary transformations of $L ^ { 2 } ( \mathbf{R} ^ { n } )$ generated by
j) $( M _ { T } u ) ( x ) = | \operatorname { det } T \rceil ^ { - 1 / 2 } u ( T ^ { - 1 } x )$, where $T \in \operatorname{GL} ( n , \mathbf{R} )$;
jj) partial Fourier transformations;
jjj) multiplication by $\operatorname { exp } ( i \pi \langle S x , x \rangle )$, where $S$ is a symmetric matrix. There exists a two-fold covering (the $\pi_{1}$ of both $\operatorname{ Mp } ( n )$ and $\operatorname{Sp} ( n )$ is $\bf Z$)
\begin{equation*} \pi : \operatorname { Mp} ( n ) \rightarrow \operatorname { Sp} ( n ) \end{equation*}
such that, if $\chi = \pi ( M )$ and $u$, $v$ are in $L ^ { 2 } ( \mathbf{R} ^ { n } )$, while $\mathcal{H} ( u , v )$ is their Wigner function, then
\begin{equation*} \mathcal{H} ( M u , M v ) = \mathcal{H} ( u , v ) \circ \chi ^ { - 1 }. \end{equation*}
This is Segal's formula [a9], which can be rephrased as follows. Let $a \in {\cal S} ^ { \prime } ( {\bf R} ^ { 2 n } )$ and $\chi \in \operatorname { Sp } ( n )$. There exists an $M$ in the fibre of  such that
such that
\begin{equation} \tag{a9} ( a \circ \chi ) ^ { w } = M ^ { * } a ^ { w } M. \end{equation}
In particular, the images by $\pi$ of the transformations j), jj), jjj) are, respectively, i), ii), iii). Moreover, if 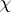 is the phase translation, $\chi ( x , \xi ) = ( x + x _ { 0 } , \xi + \xi _ { 0 } )$, (a9) is fulfilled with $M = \tau _ { x _ { 0 } , \xi _ { 0 }}$ and phase translation given by
is the phase translation, $\chi ( x , \xi ) = ( x + x _ { 0 } , \xi + \xi _ { 0 } )$, (a9) is fulfilled with $M = \tau _ { x _ { 0 } , \xi _ { 0 }}$ and phase translation given by
\begin{equation*} ( \tau _ { x _ { 0 } , \xi _ { 0 } } u ) ( y ) = u ( y - x _ { 0 } ) e ^ { 2 i \pi \langle y - x _ { 0 } / 2 , \xi _ { 0 } \rangle }. \end{equation*}
If 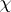 is the symmetry with respect to $( x _ { 0 } , \xi _ { 0 } )$, $M$ in (a9) is, up to a unit factor, the phase symmetry $\sigma _ { x _ { 0 } , \xi _ { 0 } }$ defined above. This yields the following composition formula:
is the symmetry with respect to $( x _ { 0 } , \xi _ { 0 } )$, $M$ in (a9) is, up to a unit factor, the phase symmetry $\sigma _ { x _ { 0 } , \xi _ { 0 } }$ defined above. This yields the following composition formula: 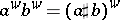 with
with
\begin{equation} \tag{a10} ( a \sharp b ) ( X ) = \end{equation}
\begin{equation*} = 2 ^ { 2 n } \int \int e ^ { - 4 i \pi [ X - Y , X - Z ] } { a } ( Y ) b ( Z ) d Y d Z , \end{equation*}
with an integral on $\mathbf{R} ^ { 2 n } \times \mathbf{R} ^ { 2 n }$. One can compare this with the classical composition formula,
\begin{equation*} \operatorname {Op} ( a ) \operatorname {Op} ( b ) = \operatorname {Op} ( a \circ b ) \end{equation*}
(cf. (a2)) with
\begin{equation*} ( a \circ b ) ( x , \xi ) = \int \int e ^ { - 2 i \pi y . \eta } a ( x , \xi + \eta ) b ( y + x , \xi ) d y d \eta, \end{equation*}
with an integral on $\mathbf{R} ^ { n } \times \mathbf{R} ^ { n }$. It is convenient to give an asymptotic version of these compositions formulas, e.g. in the semi-classical case. Let $m$ be a real number. A smooth function $a ( x , \xi , h )$ defined on $\mathbf{R} _ { x } ^ { n } \times \mathbf{R} _ { \xi } ^ { n } \times ( 0,1 ]$ is in the symbol class 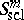 if
if
\begin{equation*} \operatorname { sup } _ {\substack{ ( x , \xi ) \in {\bf R} ^ { 2 n }}, \\{0<h\leq 1} } \left| D _ { x } ^ { \alpha } D _ { \xi } ^ { \beta } a ( x , \xi , h ) \right| h ^ { m - | \beta | } < \infty . \end{equation*}
Then one has for 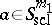 and
and 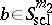 the expansion
the expansion
\begin{equation} \tag{a11} ( a \sharp b ) ( x , \xi ) = r _ { N } ( a , b ) + \end{equation}
\begin{equation*} + \sum _ { 0 \leq k < N } 2 ^ { - k } \sum _ { | \alpha | + | \beta | = k } \frac { ( - 1 ) ^ { | \beta | } } { \alpha ! \beta ! } D _ { \xi } ^ { \alpha } \partial _ { x } ^ { \beta } a D _ { \xi } ^ { \beta } \partial _ { x } ^ { \alpha } b, \end{equation*}
with $r _ { N } ( a , b ) \in S _ { \text{scl} } ^ { m _ { 1 } + m _ { 2 } - N}$. The beginning of this expansion is thus
\begin{equation*} a b + \frac { 1 } { 2 \iota} \{ a , b \}, \end{equation*}
where $\{ a , b \}$ denotes the Poisson brackets and $\iota = 2 \pi {i} $. The sums inside (a11) with $k$ even are symmetric in $a , b$ and skew-symmetric for $k$ odd. This can be compared to the classical expansion formula
\begin{equation*} ( a \circ b ) ( x , \xi ) = \sum _ { | \alpha | < N } \frac { 1 } { \alpha ! } D _ { \xi } ^ { \alpha } a \partial _ { x } ^ { \alpha } b + t _ { N } ( a , b ), \end{equation*}
with $t _ { N } ( a , b ) \in S _ { \text{scl} } ^ { m _ { 1 } + m _ { 2 } - N }$. Moreover, for $a _ { 1 } , \dots , a _ { 2k } $ in $L ^ { 1 } ( \Phi = \mathbf{R} ^ { 2 n } )$, the multiple composition formula gives
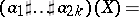 |
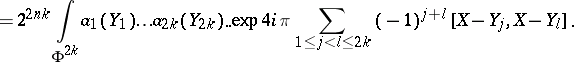 |
\begin{equation*} .d Y _ { 1 } \ldots d Y _ { 2 k }, \end{equation*}
and if $a _ { 2 k + 1 } \in L ^ { 1 } ( \Phi )$,
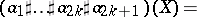 |
\begin{equation*} = 2 ^ { 2 n k } \int _ { \Phi ^ { 2 k } } a _ { 1 } ( Y _ { 1 } ) \ldots a _ { 2 k } ( Y _ { 2 k } ) \text{..} a _ { 2 k + 1 } \left( X + \sum _ { 1 \leq j < l \leq 2 k } ( - 1 ) ^ { j + l } ( Y _ { j } - Y _ { l } ) \right). \end{equation*}
\begin{equation*} .\operatorname { exp } 4 i \pi \sum _ { 1 \leq j < l \leq 2 k } ( - 1 ) ^ { j + l } [ X - Y _ { j } , X - Y _ { l } ] .. d Y _ { 1 } \ldots d Y _ { 2 k }. \end{equation*}
Consider the standard sum of homogeneous symbols defined on $\Omega \times \mathbf{R} ^ { n }$, where $\Omega$ is an open subset of ${\bf R} ^ { n }$,
\begin{equation*} a = a _ { m } + a _ { m - 1 } + r _ { m - 2 }, \end{equation*}
with $a _ { j }$ smooth on $\Omega \times \mathbf{R} ^ { n }$ and homogeneous in the following sense:
\begin{equation*} a _ { j } ( x , \lambda \xi ) = \lambda ^ { j } a _ { j } ( x , \xi ) , \text { for } | \xi | \geq 1 , \lambda \geq 1, \end{equation*}
and $r _ { m - 2} \in S _ { \text{loc} } ^ { m - 2 } ( \Omega )$, i.e. for all compact subsets $K$ of $\Omega$,
\begin{equation*} \operatorname { sup } _ { x \in K, \atop \xi \in {\bf R} ^ { n } } \left| ( D _ { x } ^ { \alpha } D _ { \xi } ^ { \beta } r _ { m - 2 } ) ( x , \xi ) \right| ( 1 + | \xi | ) ^ { 2 - m + | \beta | } < \infty. \end{equation*}
This class of pseudo-differential operators (cf. also Pseudo-differential operator) is invariant under diffeomorphisms, and using the Weyl quantization one gets that the principal symbol $a _ { m }$ is invariantly defined on the cotangent bundle $T ^ { * } ( \Omega )$ whereas the subprincipal symbol $a_{m - 1}$ is invariantly defined on the double characteristic set
\begin{equation*} \{ a _ { m } = 0 , d a _ { m } = 0 \} \end{equation*}
of the principal symbol. If one writes
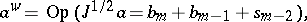 |
one gets $a = J ^ { - 1 / 2 } b$ and $a _ { m } = b _ { m }$. Moreover,
\begin{equation*} a _ { m - 1 } = b _ { m - 1 } - \frac { 1 } { 2 \iota } \sum _ { 1 \leq j \leq n } \frac { \partial ^ { 2 } b _ { m } } { \partial x _ { j } \partial \xi _ { j } } = b _ { m - 1 } ^ { s }. \end{equation*}
Thus, if one defines the subprincipal symbol as the above analytic expression $b ^ { s } _{m - 1}$ where $b = b _ { m } + b _ { m - 1} + \ldots$ is the classical symbol of $a ^ { w } = \operatorname{Op} ( b )$, one finds that this invariant $b ^ { s } _{m - 1}$ is simply the second term $a_{m - 1}$ in the expansion of the Weyl symbol $a$. In the same vein, it is also useful to note that when considering pseudo-differential operators acting on half-densities one gets a refined principal symbol $a _ { m } + a _ { m - 1 }$ invariant by diffeomorphism.
Weyl–Hörmander calculus and admissible metrics.
The developments of the analysis of partial differential operators in the 1970s required refined localizations in the phase space. E.g., the Beals–Fefferman local solvability theorem [a2] yields the geometric condition (P) as an if-and-only-if solvability condition for differential operators of principal type (with possibly complex symbols). These authors removed the analyticity assumption used by L. Nirenberg and F. Treves, and a key point in their method is a Calderón–Zygmund decomposition of the symbol, that is, a micro-localization procedure depending on a particular function, yielding a pseudo-differential calculus tailored to the symbol under investigation. Another example is provided by the Fefferman–Phong inequality [a6], establishing that second-order operators with non-negative symbols are bounded from below on $L^{2}$; a Calderón–Zygmund decomposition is needed in the proof, as well as an induction on the number of variables. These micro-localizations go much beyond the standard homogeneous calculus and also beyond the classes 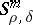 , previously called exotic. In 1979, L.V. Hörmander published [a7], providing simple and general rules for a pseudo-differential calculus to be admissible. Consider a positive-definite quadratic form $G$ defined on $\Phi$. The dual quadratic form $G ^ { \sigma }$ with respect to the symplectic structure is
, previously called exotic. In 1979, L.V. Hörmander published [a7], providing simple and general rules for a pseudo-differential calculus to be admissible. Consider a positive-definite quadratic form $G$ defined on $\Phi$. The dual quadratic form $G ^ { \sigma }$ with respect to the symplectic structure is
\begin{equation} \tag{a12} G ^ { \sigma } ( T ) = \operatorname { sup } _ { G ( U ) = 1 } [ T , U ] ^ { 2 } . \end{equation}
Define an admissible metric on the phase space as a mapping from $\Phi$ to the set of positive-definite quadratic forms on $\Phi$, $X \mapsto G _ { X }$, such that the following three properties are fulfilled:
(uncertainty principle) For all $X \in \Phi$,
\begin{equation} \tag{a13} G _ { X } \leq G _ { X } ^ { g }; \end{equation}
there exist some positive constants $\rho$, $C$, such that, for all $X , Y \in \Phi$,
\begin{equation} \tag{a14} G _ { X } ( X - Y) \leq \rho ^ { 2 } \Rightarrow G _ { Y } \leq C G _ { X }; \end{equation}
there exist some positive constants $N$, $C$, such that, for all $X , Y \in \Phi$,
\begin{equation} \tag{a15} G _ { X } \leq C ( 1 + G _ { X } ^ { \sigma } ( X - Y ) ) ^ { N } G _ { Y }. \end{equation}
Property (a13) is clearly related to the uncertainty principle, since for each $X$ one can diagonalize the quadratic form $G _ { X }$ in a symplectic basis so that
\begin{equation*} G _ { X } = \sum _ { 1 \leq j \leq n } h _ { j } ( | d q _ { j } | ^ { 2 } + | d p _ { j } | ^ { 2 } ), \end{equation*}
where $( q_j , p _ { j } )$ is a set of symplectic coordinates. One then gets
\begin{equation*} G _ { X } ^ { g } = \sum _ { 1 \leq j \leq n } h _ { j } ^ { - 1 } ( | d q _ { j } | ^ { 2 } + | d p _ { j } | ^ { 2 } ). \end{equation*}
Condition (a13) thus means that $\operatorname{max} h_{j} \leq 1$, which can be rephrased in the familiarly vague version as
\begin{equation*} \Delta p _ { j } \Delta q_j \sim h _ { j } ^ { - 1 } \geq 1 \end{equation*}
in the $G$-balls. This condition is relevant to any micro-localization procedure. When $G = G ^ { \sigma }$, one says that the quadratic form is symplectic. Property (a14) is called slowness of the metric and is usually easy to verify. Property (a15) is the temperance of the metric and is more of a technical character, although very important in handling non-local terms in the composition formula. In particular, this property is useful to verify the assumptions of Cotlar's lemma. Moreover, one defines a weight $m$ as a positive function on $\Phi$ such that there exist positive constants $C$, $N$ so that for all $X , Y \in \Phi$,
\begin{equation} \tag{a16} m ( X ) \leq C ( 1 + G _ { X } ^ { \sigma } ( X - Y ) ) ^ { N } m ( Y ), \end{equation}
and
\begin{equation} \tag{a17} G _ { X } ( X - Y ) \leq C ^ { - 1 } \Rightarrow C ^ { - 1 } \leq \frac { m ( X ) } { m ( Y ) } \leq C. \end{equation}
Eventually, one defines the class of symbols $S ( m , G )$ as the $C ^ { \infty }$-functions $a$ on the phase space such that
\begin{equation} \tag{a18} \operatorname { sup } _ { X \in \Phi } \| a ^ { ( k ) } ( X ) \| _ { G _ { X } } m ( X ) ^ { - 1 } < \infty. \end{equation}
It is, for instance, easily checked that
\begin{equation*} S _ { \rho , \delta } ^ { \mu } = S \left( \langle \xi \rangle ^ { \mu } , \langle \xi \rangle ^ { 2 \delta } | d x | ^ { 2 } + \langle \xi \rangle ^ { - 2 \rho } | d \xi | ^ { 2 } \right), \end{equation*}
with $\langle \xi \rangle = 1 + | \xi |$ and that this metric is an admissible metric when $0 \leq \delta \leq \rho \leq 1$, $\delta < 1$. The metric defining $S _ { 1,1 } ^ { 0 }$ satisfies (a13)–(a14) but fails to satisfy (a15). Indeed, there are counterexamples showing that for the classical and the Weyl quantization [a4] there are symbols in $S _ { 1,1 } ^ { 0 }$ whose quantization is not $L^{2}$-bounded. In fact, one of the building block for the calculus of pseudo-differential operators is the $L^{2}$-boundedness of the Weyl quantization of symbols in $S ( 1 , G )$, where $G$ is an admissible metric. One defines the Planck function of the calculus as
\begin{equation} \tag{a19} H ( X ) = \operatorname { sup } _ { T \neq 0 } \sqrt { \frac { G _{X} ( T ) } { G _ { X } ^ { \sigma } ( T ) } } \end{equation}
and notes that from (a13), $H ( X ) \leq 1$. One obtains the composition formula (a11) with $\alpha \in S ( m _ { 1 } , G )$, $b \in S ( m _ { 2 } , G )$ and $r _ { N } ( a , b ) \in S ( m _ { 1 } m _ { 2 } H ^ { N } , G )$. In particular, one obtains, with obvious notations,
\begin{equation*} a \sharp b \in S ( m _ { 1 } m _ { 2 } , G ), \end{equation*}
\begin{equation*} a \sharp b = a b + S ( m _ { 1 } m _ { 2 } H , G ) ,\; a \sharp b = a b + \frac { 1 } { 2 \iota } \{ a , b \} + S ( m _ { 1 } m _ { 2 } H ^ { 2 } , G ), \end{equation*}
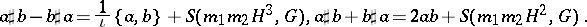 |
The Fefferman–Phong inequality has also a simple expression in this framework: Let $a$ be a non-negative symbol in $S ( H ^ { - 2 } , G )$, then the operator 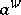 is semi-bounded from below in $L ^ { 2 } ( \mathbf{R} ^ { n } )$. The proof uses a Calderón–Zygmund decomposition and in fact one shows that $a \in S ( h ^ { - 2 } , g )$, where $h$ is the Planck function related to the admissible metric $g$ defined by
is semi-bounded from below in $L ^ { 2 } ( \mathbf{R} ^ { n } )$. The proof uses a Calderón–Zygmund decomposition and in fact one shows that $a \in S ( h ^ { - 2 } , g )$, where $h$ is the Planck function related to the admissible metric $g$ defined by
\begin{equation*} g_{X} ( T ) = \frac { G _ { X } ( T ) } { H ( X ) [ 1 + a ( X ) + H ( X ) ^ { 2 } \| a ^ { \prime \prime } ( X ) \| ^ { 2 _{ G _ { X }}} ] ^ { 1 / 2 } }. \end{equation*}
On the other hand, if $G$ is an admissible metric and $q _ { \alpha } \in S ( H ^ { - 1 } , G )$ uniformly with respect to a parameter $\alpha$, the following metric also satisfies (a13)–(a15): $\tilde { g } _ { X } = H ( X ) ^ { - 1 } \tilde { h } ( X ) G _ { X } ( T )$, with
\begin{equation*} \widetilde { h } ( X ) ^ { - 1 } = 1 + \operatorname { sup } _ { \alpha } | q _ { \alpha } ( X ) | + H ( X ) \operatorname { sup } _ { \alpha } \| q _ { \alpha } ^ { \prime } ( X ) \| _ { G _ { X } } ^ { 2 }. \end{equation*}
One gets in this case that $q _ { \alpha } \in S ( \tilde { h } ^ { - 1 } , \tilde{g} )$ uniformly. A key point in the Beals–Fefferman proof of local solvability under condition (P) can be reformulated through the construction of the previous metric. Sobolev spaces related to this type of calculus were studied in [a1] (cf. also Sobolev space). For an admissible metric $G$ and a weight $m$, the space $H ( m , G )$ is defined as
\begin{equation*} \{ u \in \mathcal{S} ^ { \prime } ( \mathbf{R} ^ { n } ) : \forall a \in S ( m , G ) , a ^ { w } u \in L ^ { 2 } ( \mathbf{R} ^ { n } ) \}. \end{equation*}
It can be proven that a Hilbertian structure can be set on $H ( m , G )$, that $H ( 1 , G ) = L ^ { 2 } ( \mathbf{R} ^ { n } )$ and that for $a \in S ( m , G )$ and $m_1$ another weight, the mapping
\begin{equation*} a ^ { w } : H ( m m _ { 1 } , G ) \rightarrow H ( m _ { 1 } , G ) \end{equation*}
is continuous.
Further developments of the Weyl calculus were explored in [a3], with higher-order micro-localizations. Several metrics
\begin{equation*} g _ { 1 } \leq \ldots \leq g _ { k } \end{equation*}
are given on the phase space. All these metrics satisfy (a13)–(a14), but, except for $g_1$, fail to satisfy globally the temperance condition (a15). Instead, the metric $g_{l+ 1}$ is assumed to be (uniformly) temperate on the $g_{l}$-balls. It is then possible to produce a satisfactory quantization formula for symbols belonging to a class $S ( m , g _ { k } )$. A typical example is given in [a5], with applications to propagation of singularities for non-linear hyperbolic equations:
\begin{equation*} g _ { 1 } = | d x | ^ { 2 } + \frac { | d \xi | ^ { 2 } } { | \xi | ^ { 2 } } \leq g_2 = \frac { | d x | ^ { 2 } } { | x | ^ { 2 } } + \frac { | d \xi | ^ { 2 } } { | \xi | ^ { 2 } }, \end{equation*}
where $g_1$ is defined on $| \xi | > 1$, and $g_{2}$ on
\begin{equation*} \{ | x | < 1 , | x | | \xi | > 1 \} \end{equation*}
It is then possible to quantize functions $a ( x , \xi )$ homogeneous of degree $\mu$ in the variable $x$, and $\nu$ in the variable $\xi $, so as to get composition formulas, Sobolev spaces, and the standard pseudo-differential apparatus allowing a commutator argument to work for propagation results.
References
| [a1] | J.-M. Bony, J.-Y. Chemin, "Espaces fonctionnels associés au calcul de Weyl–Hörmander" Bull. Soc. Math. France , 122 (1994) pp. 77–118 Zbl 0798.35172 |
| [a2] | R. Beals, C. Fefferman, "On local solvability of linear partial differential equations" Ann. of Math. , 97 (1973) pp. 482–498 MR0352746 Zbl 0256.35002 |
| [a3] | J.-M. Bony, N. Lerner, "Quantification asymtotique et microlocalisations d'ordre supérieur" Ann. Sci. Ecole Norm. Sup. , 22 (1989) pp. 377–483 |
| [a4] | A. Boulkhemair, "Remarque sur la quantification de Weyl pour la classe de symboles $S _ { 1,1 } ^ { 0 }$" C.R. Acad. Sci. Paris , 321 : 8 (1995) pp. 1017–1022 MR1360564 Zbl 0842.35144 |
| [a5] | J.-M. Bony, "Second microlocalization and propagation of singularities for semi-linear hyperbolic equations" K. Mizohata (ed.) , Hyperbolic Equations and Related Topics , Kinokuniya (1986) pp. 11–49 MR925240 |
| [a6] | C. Fefferman, D.H. Phong, "On positivity of pseudo-differential operators" Proc. Nat. Acad. Sci. USA , 75 (1978) pp. 4673–4674 MR0507931 Zbl 0391.35062 |
| [a7] | L. Hörmander, "The Weyl calculus of pseudo-differential operators" Commun. Pure Appl. Math. , 32 (1979) pp. 359–443 MR517939 Zbl 0388.47032 |
| [a8] | L. Hörmander, "The analysis of linear partial differential operators III-IV" , Springer (1985) |
| [a9] | I. Segal, "Transforms for operators and asymptotic automorphisms over a locally compact abelian group" Math. Scand. , 13 (1963) pp. 31–43 |
| [a10] | A. Unterberger, "Oscillateur harmonique et opérateurs pseudo-différentiels" Ann. Inst. Fourier , 29 : 3 (1979) pp. 201–221 MR0552965 Zbl 0396.47027 |
| [a11] | A. Weil, "Sur certains groupes d'opérateurs unitaires" Acta Math. , 111 (1964) pp. 143–211 MR0165033 |
| [a12] | H. Weyl, "Gruppentheorie und Quantenmechanik" , S. Hirzel (1928) MR0450450 Zbl 54.0954.03 |
Weyl quantization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_quantization&oldid=18270