Difference between revisions of "Fredholm eigenvalue of a Jordan curve"
(Importing text file) |
(details) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 75 formulas, 72 were replaced by TEX code.--> | |
| − | be the | + | {{TEX|semi-auto}}{{TEX|part}} |
| + | Let $C$ be a smooth [[Jordan curve|Jordan curve]] (of class $C ^ { 3 }$) in the complex $z = ( x + i y )$-plane, $G$ its interior, $G ^ { * }$ its exterior. Then, let | ||
| − | + | \begin{equation*} K ( x , t ) = - \frac { 1 } { \pi } \frac { \partial } { \partial n _ { t } } \operatorname { log } | z - t | , z , t \in C, \end{equation*} | |
| − | + | be the corresponding classical Neumann kernel with $n_t$ the interior normal. The Fredholm eigenvalue $\lambda$ of $C$ is the smallest eigenvalue $> 1$ of this kernel. | |
| − | + | This eigenvalue plays an important role for the speed of the successive approximation solution of several problems, such as the integral equation with this kernel corresponding to the [[Dirichlet problem|Dirichlet problem]] and several integral equations to construct the conformal Riemann mapping function of $G$ [[#References|[a1]]]. | |
| − | + | For arbitrary Jordan curves $C$, there is the following characterization of the Fredholm eigenvalue $\lambda$ [[#References|[a4]]]: | |
| − | + | \begin{equation*} \frac { 1 } { \lambda } = \operatorname { sup } \frac { | D ( h ) - D ^ { * } ( h ) | } { D ( h ) + D ^ { * } ( h ) }, \end{equation*} | |
| − | + | where the supremum is over all functions $h$ that are continuous in the extended plane and harmonic in $G$ and in $G ^ { * }$, with corresponding Dirichlet integrals $D ( h )$ and $D ^ { * } ( h )$ (cf. also [[Dirichlet integral|Dirichlet integral]]). | |
| − | + | One has: $1 \leq \lambda \leq \infty$, with $\lambda = \infty$ if and only if $C$ is a circle, and with $\lambda > 1$ if and only if $C$ is a quasi-circle [[#References|[a4]]], [[#References|[a2]]]. In some sense, $\lambda$ is a measure for the deviation of $C$ from a circle. $\lambda$ is invariant under Möbius transformations (cf. also [[Fractional-linear mapping|Fractional-linear mapping]]). | |
| − | + | The exact value of $\lambda$ is known for several special Jordan curves: e.g. ellipses, some Cassinians, triangles, regular $n$-gons, and rectangles close to a square. | |
| − | + | There is also the following characterization of $\lambda$, using the Riemann mapping of $G ^ { * }$. Without loss of generality one may assume that $G ^ { * }$ is the image of $| \zeta | > 1$ under a univalent conformal mapping (cf. also [[Conformal mapping|Conformal mapping]]) $z ( \zeta )$ of the form | |
| − | + | \begin{equation*} z ( \zeta ) = \zeta + \frac { a _ { 1 } } { \zeta } + \frac { a _ { 2 } } { \zeta ^ { 2 } } + \ldots \end{equation*} | |
| − | + | One can then calculate the so-called Grunsky coefficients <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120140/f12014036.png"/> in the development | |
| + | |||
| + | \begin{equation*} \operatorname { log } \frac { z ( \zeta ) - z ( \zeta ^ { \prime } ) } { \zeta - \zeta ^ { \prime } } = - \sum _ { k , l = 1 } ^ { \infty } a _ { k l } \zeta ^ { - k } \zeta ^ { \prime - l }, \end{equation*} | ||
| + | |||
| + | \begin{equation*} | \zeta | > 1 , | \zeta ^ { \prime } | > 1. \end{equation*} | ||
Then | Then | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120140/f12014039.png"/></td> </tr></table> |
| − | where the supremum is taken over all complex numbers | + | where the supremum is taken over all complex numbers $x _ { k }$ with $\sum _ { k = 1 } ^ { \infty } | x _ { k } | ^ { 2 } / k = 1$. This gives also a procedure to evaluate $\lambda$ numerically [[#References|[a2]]]. |
| − | Hence one obtains simple upper estimates for | + | Hence one obtains simple upper estimates for $\lambda$, of course. There are many other such estimates in which the mapping $z ( \zeta )$ is involved [[#References|[a2]]]. As a simple consequence, there is the following very useful inequality for Jordan curves $C$ with corners [[#References|[a2]]]: |
| − | + | \begin{equation*} \frac { 1 } { \lambda } \geq | 1 - \alpha |. \end{equation*} | |
| − | Here, | + | Here, $\alpha \pi$ denotes the angle at the corner. |
| − | For large | + | For large $\lambda$ one finds [[#References|[a2]]] that $C$ must be contained in an annulus with radii $r$ and $r ( 1 + 2.78 / \lambda )$ such that $C$ separates the boundary circles with these radii. However, in the other direction, $\lambda$ can be close to $1$ even though $C$ lies, in the same manner, in an annulus for which the quotient of the radii is arbitrarily close to $1$. |
| − | There are also several lower estimates from M. Schiffer and others for | + | There are also several lower estimates from M. Schiffer and others for $\lambda$ [[#References|[a1]]], [[#References|[a2]]], [[#References|[a4]]]. If, for example, $C$ is the image of $| \zeta | = 1$ under a univalent conformal mapping of an annulus $r < | \zeta | < R$ ($r < 1 < R$), then |
| − | + | \begin{equation*} \lambda \geq \frac { r ^ { 2 } + R ^ { 2 } } { 1 + ( r R ) ^ { 2 } }. \end{equation*} | |
| − | L.V. Ahlfors noted a remarkable interaction between the theory of Fredholm eigenvalues and the theory of [[Quasi-conformal mapping|quasi-conformal mapping]]: If there is a | + | L.V. Ahlfors noted a remarkable interaction between the theory of Fredholm eigenvalues and the theory of [[Quasi-conformal mapping|quasi-conformal mapping]]: If there is a $Q$-quasi-conformal reflection at $C$ (i.e., a sense-reversing $Q$-quasi-conformal mapping of the extended plane which leaves $C$ pointwise fixed), then [[#References|[a2]]], [[#References|[a4]]] |
| − | + | \begin{equation*} \lambda \geq \frac { Q + 1 } { Q - 1 }. \end{equation*} | |
The question of equality gives rise to interesting connections with the theory of extremal quasi-conformal mappings (connected with the names of O. Teichmüller, K. Strebel, E. Reich; cf. [[#References|[a2]]]). | The question of equality gives rise to interesting connections with the theory of extremal quasi-conformal mappings (connected with the names of O. Teichmüller, K. Strebel, E. Reich; cf. [[#References|[a2]]]). | ||
| Line 53: | Line 61: | ||
From this Ahlfors inequality one obtains almost immediately [[#References|[a2]]], [[#References|[a4]]]: | From this Ahlfors inequality one obtains almost immediately [[#References|[a2]]], [[#References|[a4]]]: | ||
| − | + | \begin{equation*} \frac { 1 } { \lambda } \leq \operatorname { max } _ { \varphi } | \operatorname { cos } \alpha ( \varphi ) | \end{equation*} | |
| − | if | + | if $C$ is smooth and starlike with respect to the interior point $z = 0$, where $\alpha ( \varphi )$ denotes the angle between the ray $\operatorname{arg} z = \varphi$ and the tangent at the point of $C$ with $\varphi$. |
For a theory of Fredholm eigenvalues for multiply-connected domains, see [[#References|[a3]]]. | For a theory of Fredholm eigenvalues for multiply-connected domains, see [[#References|[a3]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> D. Gaier, "Konstruktive Methoden der konformen Abbildung" , Springer (1964)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> R. Kühnau, "Möglichst konforme Spiegelung an einer Jordankurve" ''Jahresber. Deutsch. Math. Ver.'' , '''90''' (1988) pp. 90–109</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> M. Schiffer, "Fredholm eigenvalues of multiply-connected domains" ''Pacific J. Math.'' , '''9''' (1959) pp. 211–269</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> G. Schober, "Estimates for Fredholm eigenvalues based on quasiconformal mapping" , ''Lecture Notes Math.'' , '''333''' , Springer (1973) pp. 211–217</td></tr></table> |
Latest revision as of 20:48, 23 January 2024
Let $C$ be a smooth Jordan curve (of class $C ^ { 3 }$) in the complex $z = ( x + i y )$-plane, $G$ its interior, $G ^ { * }$ its exterior. Then, let
\begin{equation*} K ( x , t ) = - \frac { 1 } { \pi } \frac { \partial } { \partial n _ { t } } \operatorname { log } | z - t | , z , t \in C, \end{equation*}
be the corresponding classical Neumann kernel with $n_t$ the interior normal. The Fredholm eigenvalue $\lambda$ of $C$ is the smallest eigenvalue $> 1$ of this kernel.
This eigenvalue plays an important role for the speed of the successive approximation solution of several problems, such as the integral equation with this kernel corresponding to the Dirichlet problem and several integral equations to construct the conformal Riemann mapping function of $G$ [a1].
For arbitrary Jordan curves $C$, there is the following characterization of the Fredholm eigenvalue $\lambda$ [a4]:
\begin{equation*} \frac { 1 } { \lambda } = \operatorname { sup } \frac { | D ( h ) - D ^ { * } ( h ) | } { D ( h ) + D ^ { * } ( h ) }, \end{equation*}
where the supremum is over all functions $h$ that are continuous in the extended plane and harmonic in $G$ and in $G ^ { * }$, with corresponding Dirichlet integrals $D ( h )$ and $D ^ { * } ( h )$ (cf. also Dirichlet integral).
One has: $1 \leq \lambda \leq \infty$, with $\lambda = \infty$ if and only if $C$ is a circle, and with $\lambda > 1$ if and only if $C$ is a quasi-circle [a4], [a2]. In some sense, $\lambda$ is a measure for the deviation of $C$ from a circle. $\lambda$ is invariant under Möbius transformations (cf. also Fractional-linear mapping).
The exact value of $\lambda$ is known for several special Jordan curves: e.g. ellipses, some Cassinians, triangles, regular $n$-gons, and rectangles close to a square.
There is also the following characterization of $\lambda$, using the Riemann mapping of $G ^ { * }$. Without loss of generality one may assume that $G ^ { * }$ is the image of $| \zeta | > 1$ under a univalent conformal mapping (cf. also Conformal mapping) $z ( \zeta )$ of the form
\begin{equation*} z ( \zeta ) = \zeta + \frac { a _ { 1 } } { \zeta } + \frac { a _ { 2 } } { \zeta ^ { 2 } } + \ldots \end{equation*}
One can then calculate the so-called Grunsky coefficients  in the development
in the development
\begin{equation*} \operatorname { log } \frac { z ( \zeta ) - z ( \zeta ^ { \prime } ) } { \zeta - \zeta ^ { \prime } } = - \sum _ { k , l = 1 } ^ { \infty } a _ { k l } \zeta ^ { - k } \zeta ^ { \prime - l }, \end{equation*}
\begin{equation*} | \zeta | > 1 , | \zeta ^ { \prime } | > 1. \end{equation*}
Then
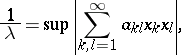 |
where the supremum is taken over all complex numbers $x _ { k }$ with $\sum _ { k = 1 } ^ { \infty } | x _ { k } | ^ { 2 } / k = 1$. This gives also a procedure to evaluate $\lambda$ numerically [a2].
Hence one obtains simple upper estimates for $\lambda$, of course. There are many other such estimates in which the mapping $z ( \zeta )$ is involved [a2]. As a simple consequence, there is the following very useful inequality for Jordan curves $C$ with corners [a2]:
\begin{equation*} \frac { 1 } { \lambda } \geq | 1 - \alpha |. \end{equation*}
Here, $\alpha \pi$ denotes the angle at the corner.
For large $\lambda$ one finds [a2] that $C$ must be contained in an annulus with radii $r$ and $r ( 1 + 2.78 / \lambda )$ such that $C$ separates the boundary circles with these radii. However, in the other direction, $\lambda$ can be close to $1$ even though $C$ lies, in the same manner, in an annulus for which the quotient of the radii is arbitrarily close to $1$.
There are also several lower estimates from M. Schiffer and others for $\lambda$ [a1], [a2], [a4]. If, for example, $C$ is the image of $| \zeta | = 1$ under a univalent conformal mapping of an annulus $r < | \zeta | < R$ ($r < 1 < R$), then
\begin{equation*} \lambda \geq \frac { r ^ { 2 } + R ^ { 2 } } { 1 + ( r R ) ^ { 2 } }. \end{equation*}
L.V. Ahlfors noted a remarkable interaction between the theory of Fredholm eigenvalues and the theory of quasi-conformal mapping: If there is a $Q$-quasi-conformal reflection at $C$ (i.e., a sense-reversing $Q$-quasi-conformal mapping of the extended plane which leaves $C$ pointwise fixed), then [a2], [a4]
\begin{equation*} \lambda \geq \frac { Q + 1 } { Q - 1 }. \end{equation*}
The question of equality gives rise to interesting connections with the theory of extremal quasi-conformal mappings (connected with the names of O. Teichmüller, K. Strebel, E. Reich; cf. [a2]).
From this Ahlfors inequality one obtains almost immediately [a2], [a4]:
\begin{equation*} \frac { 1 } { \lambda } \leq \operatorname { max } _ { \varphi } | \operatorname { cos } \alpha ( \varphi ) | \end{equation*}
if $C$ is smooth and starlike with respect to the interior point $z = 0$, where $\alpha ( \varphi )$ denotes the angle between the ray $\operatorname{arg} z = \varphi$ and the tangent at the point of $C$ with $\varphi$.
For a theory of Fredholm eigenvalues for multiply-connected domains, see [a3].
References
| [a1] | D. Gaier, "Konstruktive Methoden der konformen Abbildung" , Springer (1964) |
| [a2] | R. Kühnau, "Möglichst konforme Spiegelung an einer Jordankurve" Jahresber. Deutsch. Math. Ver. , 90 (1988) pp. 90–109 |
| [a3] | M. Schiffer, "Fredholm eigenvalues of multiply-connected domains" Pacific J. Math. , 9 (1959) pp. 211–269 |
| [a4] | G. Schober, "Estimates for Fredholm eigenvalues based on quasiconformal mapping" , Lecture Notes Math. , 333 , Springer (1973) pp. 211–217 |
Fredholm eigenvalue of a Jordan curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fredholm_eigenvalue_of_a_Jordan_curve&oldid=17984