Difference between revisions of "Reidemeister theorem"
(Importing text file) |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Two link diagrams represent the same ambient isotopy class of a link in | + | {{TEX|done}}{{MSC|57K}} |
| + | |||
| + | Two link diagrams represent the same ambient isotopy class of a link in $S^3$ if and only if they are related by a finite number of Reidemeister moves (see Fig. a1) and a plane isotopy. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r130060a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r130060a.gif" /> | ||
| Line 5: | Line 7: | ||
Figure: r130060a | Figure: r130060a | ||
| − | Proofs of the theorem were published in 1927 by K. Reidemeister | + | Proofs of the theorem were published in 1927 by K. Reidemeister {{Cite|a3}}, and by J.W. Alexander and G.B. Briggs {{Cite|a1}}. |
| − | The theorem also holds for oriented links and oriented diagrams, provided that Reidemeister moves observe the orientation of diagrams. It holds also for links in a manifold | + | The theorem also holds for oriented links and oriented diagrams, provided that Reidemeister moves observe the orientation of diagrams. It holds also for links in a manifold $M=F\times[0,1]$, where $F$ is a surface. |
| − | The first formalization of knot theory was obtained by M. Dehn and P. Heegaard by introducing lattice knots and lattice moves | + | The first formalization of knot theory was obtained by M. Dehn and P. Heegaard by introducing lattice knots and lattice moves {{Cite|a2}}. Every knot has a lattice knot representation and two knots are lattice equivalent if and only if they are ambient isotopic. The Reidemeister approach was to consider polygonal knots up to $\Delta$-moves. (A $\Delta$-move replaces one side of a triangle by two other sides or vice versa. A regular projection of a $\Delta$-move can be decomposed into Reidemeister moves.) This approach was taken by Reidemeister to prove his theorem. |
====References==== | ====References==== | ||
| − | + | * {{Ref|a1}} J.W. Alexander, G.B. Briggs, "On types of knotted curves" ''Ann. of Math.'' , '''28''' : 2 (1927/28) pp. 563–586 {{ZBL|53.0549.02}} | |
| + | * {{Ref|a2}} M. Dehn, P. Heegaard, "Analysis situs" , ''Encykl. Math. Wiss.'' , '''III AB3''' , Leipzig (1907) pp. 153–220 {{ZBL|38.0510.14}} | ||
| + | * {{Ref|a3}} K. Reidemeister, "Elementare Begrundung der Knotentheorie" ''Abh. Math. Sem. Univ. Hamburg'' , '''5''' (1927) pp. 24–32 {{ZBL|52.0579.01}} | ||
Latest revision as of 20:23, 16 March 2023
2020 Mathematics Subject Classification: Primary: 57K [MSN][ZBL]
Two link diagrams represent the same ambient isotopy class of a link in $S^3$ if and only if they are related by a finite number of Reidemeister moves (see Fig. a1) and a plane isotopy.
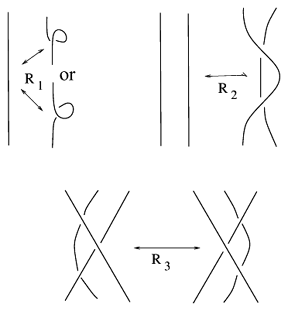
Figure: r130060a
Proofs of the theorem were published in 1927 by K. Reidemeister [a3], and by J.W. Alexander and G.B. Briggs [a1].
The theorem also holds for oriented links and oriented diagrams, provided that Reidemeister moves observe the orientation of diagrams. It holds also for links in a manifold $M=F\times[0,1]$, where $F$ is a surface.
The first formalization of knot theory was obtained by M. Dehn and P. Heegaard by introducing lattice knots and lattice moves [a2]. Every knot has a lattice knot representation and two knots are lattice equivalent if and only if they are ambient isotopic. The Reidemeister approach was to consider polygonal knots up to $\Delta$-moves. (A $\Delta$-move replaces one side of a triangle by two other sides or vice versa. A regular projection of a $\Delta$-move can be decomposed into Reidemeister moves.) This approach was taken by Reidemeister to prove his theorem.
References
- [a1] J.W. Alexander, G.B. Briggs, "On types of knotted curves" Ann. of Math. , 28 : 2 (1927/28) pp. 563–586 Zbl 53.0549.02
- [a2] M. Dehn, P. Heegaard, "Analysis situs" , Encykl. Math. Wiss. , III AB3 , Leipzig (1907) pp. 153–220 Zbl 38.0510.14
- [a3] K. Reidemeister, "Elementare Begrundung der Knotentheorie" Abh. Math. Sem. Univ. Hamburg , 5 (1927) pp. 24–32 Zbl 52.0579.01
Reidemeister theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reidemeister_theorem&oldid=16693