Difference between revisions of "Paracompact space"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | A [[Topological space|topological space]] in which any open covering (cf. [[Covering (of a set)|Covering (of a set)]]) can be refined to a locally finite open covering. (A collection | + | {{TEX|done}} |
| + | A [[Topological space|topological space]] in which any open covering (cf. [[Covering (of a set)|Covering (of a set)]]) can be refined to a locally finite open covering. (A collection $\gamma$ of subsets of a topological space $X$ is called locally finite in $X$ if each point $x\in X$ has a neighbourhood in $X$ which intersects only finitely many elements of the collection $\gamma$; a collection $\gamma$ of subsets is a refinement of a collection $\lambda$ if each element of the collection $\gamma$ is contained in some element of the collection $\lambda$.) A paracompact [[Hausdorff space|Hausdorff space]] is called a paracompactum. The class of paracompacta is very extensive — it includes all metric spaces (Stone's theorem) and all Hausdorff compacta. However, not every locally compact Hausdorff space is paracompact. | ||
| − | The significance of paracompactness is shown by the clear generality of this concept and by a number of remarkable properties of paracompacta. First of all, each paracompact Hausdorff space is normal (cf. [[Normal space|Normal space]]). This permits the construction in paracompacta of a partition of unity subordinate to an arbitrary given open covering | + | The significance of paracompactness is shown by the clear generality of this concept and by a number of remarkable properties of paracompacta. First of all, each paracompact Hausdorff space is normal (cf. [[Normal space|Normal space]]). This permits the construction in paracompacta of a partition of unity subordinate to an arbitrary given open covering $\gamma$. That is, a collection of real non-negative continuous functions on the space subject to the following conditions: a) the collection of supports of these functions is locally finite and is a refinement of $\gamma$; and b) at each point of the space, the sum of the values, at that point, of all those functions of the set which are different at it from zero (there are only finitely many such functions) is equal to one. Partitions of unity are basic tools for the construction of immersions of spaces in standard spaces. In particular, they are used for imbedding manifolds in Euclidean spaces and for the proof of the theorem about the metrizability of each [[Tikhonov space|Tikhonov space]] with a $\sigma$-locally finite base. Moreover, in the theory of manifolds partitions of unity form the basis of methods with the help of which a simultaneous synthesis of local constructions is obtained, after first constructing within the boundaries of individual charts objects with certain desired properties (in particular, for vector or tensor fields). Therefore one of the requirements assumed in the theory of manifolds is the requirement of paracompactness, which is not superfluous since there exist non-paracompact connected Hausdorff spaces, which are locally like $\mathbf R^n$. |
In the presence of paracompactness some local properties are synthesized and fulfilled globally. In particular, if a paracompactum is locally metrizable, then it is metrizable; if a Hausdorff space is locally complete in the sense of Čech and paracompact, then it is complete in the sense of Čech. In [[Dimension theory|dimension theory]], a number of important relations for paracompacta have been obtained which do not even extend to normal spaces. This is not surprising since one of the basic definitions of dimension — due to Lebesgue and connected with the examination of the multiplicity of open coverings, is plainly related to the concept of local finiteness and this is basic to the definition of paracompactness. | In the presence of paracompactness some local properties are synthesized and fulfilled globally. In particular, if a paracompactum is locally metrizable, then it is metrizable; if a Hausdorff space is locally complete in the sense of Čech and paracompact, then it is complete in the sense of Čech. In [[Dimension theory|dimension theory]], a number of important relations for paracompacta have been obtained which do not even extend to normal spaces. This is not surprising since one of the basic definitions of dimension — due to Lebesgue and connected with the examination of the multiplicity of open coverings, is plainly related to the concept of local finiteness and this is basic to the definition of paracompactness. | ||
| Line 7: | Line 8: | ||
Paracompactness is not inherited by arbitrary subspaces (in which it differs from metrizability), otherwise, for example, all Tikhonov spaces, as subspaces of Hausdorff compacta, would be paracompact. However, each closed subspace of a paracompactum is a paracompactum. An important shortfall of paracompactness is its lack of multiplicativity: The product of two paracompacta need not be a paracompactum. On the other hand, in the class of Hausdorff spaces, the inverse image of a paracompactum under a [[Perfect mapping|perfect mapping]] is a paracompactum, and the image of a paracompactum under a continuous [[Closed mapping|closed mapping]] is a paracompactum. Lindelöf spaces (cf. [[Lindelöf space|Lindelöf space]]) are, in particular, paracompacta. For the space of all continuous real functions on an arbitrary Tikhonov space, with the topology of pointwise convergence, paracompactness is equivalent to the space being Lindelöf. If a Banach space in the weak topology is topologically generated by some compactum lying within it, then it is paracompact. An important example of paracompacta are the polyhedra underlying CW-complexes. | Paracompactness is not inherited by arbitrary subspaces (in which it differs from metrizability), otherwise, for example, all Tikhonov spaces, as subspaces of Hausdorff compacta, would be paracompact. However, each closed subspace of a paracompactum is a paracompactum. An important shortfall of paracompactness is its lack of multiplicativity: The product of two paracompacta need not be a paracompactum. On the other hand, in the class of Hausdorff spaces, the inverse image of a paracompactum under a [[Perfect mapping|perfect mapping]] is a paracompactum, and the image of a paracompactum under a continuous [[Closed mapping|closed mapping]] is a paracompactum. Lindelöf spaces (cf. [[Lindelöf space|Lindelöf space]]) are, in particular, paracompacta. For the space of all continuous real functions on an arbitrary Tikhonov space, with the topology of pointwise convergence, paracompactness is equivalent to the space being Lindelöf. If a Banach space in the weak topology is topologically generated by some compactum lying within it, then it is paracompact. An important example of paracompacta are the polyhedra underlying CW-complexes. | ||
| − | In the class of paracompacta the metrizability conditions are simplified. In particular, a paracompactum is metrizable if and only if it possesses a base of countable order, i.e. a base such that any decreasing sequence of elements of it containing an arbitrary point | + | In the class of paracompacta the metrizability conditions are simplified. In particular, a paracompactum is metrizable if and only if it possesses a base of countable order, i.e. a base such that any decreasing sequence of elements of it containing an arbitrary point $x\in X$ forms a base at that point. There are many [[Paracompactness criteria|paracompactness criteria]]. In particular, for a Tikhonov space $X$ the following conditions are equivalent: a) $X$ is paracompact; b) any open covering of $X$ can be refined to a locally finite covering; c) any open covering of $X$ can be refined to a $\sigma$-locally finite open covering; and d) any open covering of $X$ can be refined to a conservative closed covering, i.e. to a covering such that the union of any subcollection of it is closed in $X$. |
| − | The following criterion is important: A Tikhonov space is paracompact if and only if each open covering | + | The following criterion is important: A Tikhonov space is paracompact if and only if each open covering $\gamma$ of it has an open star refinement $\lambda$; the latter means that for each point $x\in X$ the union of all elements of $\lambda$ containing $x$ is contained in some element of $\gamma$. The concept of star refinability serves as an expression of the idea of unlimited division of a space, and can be interpreted as the most general set-theoretical form of the triangle axiom. |
====References==== | ====References==== | ||
| Line 21: | Line 22: | ||
Conservative collections are also called closure-preserving; star refinements are also called barycentric refinements. | Conservative collections are also called closure-preserving; star refinements are also called barycentric refinements. | ||
| − | There are a number of variations of the theme of paracompactness. To describe those, a number of concepts of coverings are needed. A family of sets is called disjoint if its elements are mutually disjoint. A | + | There are a number of variations of the theme of paracompactness. To describe those, a number of concepts of coverings are needed. A family of sets is called disjoint if its elements are mutually disjoint. A $\sigma$-disjoint covering is a countable union of disjoint coverings. A point-finite covering $\gamma$ of a space $X$ is such that each $x\in X$ is contained in only finitely many elements of $\gamma$. A $\sigma$-point-finite covering is a countable union of point-finite ones. A covering $\gamma$ is star-finite, respectively star-countable, if each element of $\gamma$ intersects only finitely many, respectively countably many, others. |
| − | A space is called strongly paracompact if each open covering has an open star-finite refinement; it is called weakly paracompact, respectively | + | A space is called strongly paracompact if each open covering has an open star-finite refinement; it is called weakly paracompact, respectively $\sigma$-metacompact, if each open covering has an open star-finite, respectively $\sigma$-star-finite, refinement. A space is called screened if every open covering has a $\sigma$-disjoint open refinement. A space is hereditarily paracompact if every subspace is paracompact. A space is star-normal or star-paracompact if every open covering has an open star refinement. It is countably paracompact if every open covering has an open locally compact refinement; it is $\tau$-paracompact, where $\tau$ is a cardinal number, if the same holds for open coverings of cardinality $\leq\tau$. For more details and relations of all these variations with each other and other topological properties cf. [[#References|[2]]]. Paracompactness itself remains the central notion. |
As remarked above, paracompactness is a very natural and useful property. It is therefore most unfortunate that the property is not inherited by subspaces and products. In the case of another concept (than topological space) to capture ideas of near and convergence, the so-called nearness spaces, this drawback disappears; cf. [[#References|[a1]]] and [[Topological structures|Topological structures]]. For the notion "complete in the sense of Čech" cf. [[Complete space|Complete space]]. | As remarked above, paracompactness is a very natural and useful property. It is therefore most unfortunate that the property is not inherited by subspaces and products. In the case of another concept (than topological space) to capture ideas of near and convergence, the so-called nearness spaces, this drawback disappears; cf. [[#References|[a1]]] and [[Topological structures|Topological structures]]. For the notion "complete in the sense of Čech" cf. [[Complete space|Complete space]]. | ||
Latest revision as of 14:04, 30 July 2014
A topological space in which any open covering (cf. Covering (of a set)) can be refined to a locally finite open covering. (A collection $\gamma$ of subsets of a topological space $X$ is called locally finite in $X$ if each point $x\in X$ has a neighbourhood in $X$ which intersects only finitely many elements of the collection $\gamma$; a collection $\gamma$ of subsets is a refinement of a collection $\lambda$ if each element of the collection $\gamma$ is contained in some element of the collection $\lambda$.) A paracompact Hausdorff space is called a paracompactum. The class of paracompacta is very extensive — it includes all metric spaces (Stone's theorem) and all Hausdorff compacta. However, not every locally compact Hausdorff space is paracompact.
The significance of paracompactness is shown by the clear generality of this concept and by a number of remarkable properties of paracompacta. First of all, each paracompact Hausdorff space is normal (cf. Normal space). This permits the construction in paracompacta of a partition of unity subordinate to an arbitrary given open covering $\gamma$. That is, a collection of real non-negative continuous functions on the space subject to the following conditions: a) the collection of supports of these functions is locally finite and is a refinement of $\gamma$; and b) at each point of the space, the sum of the values, at that point, of all those functions of the set which are different at it from zero (there are only finitely many such functions) is equal to one. Partitions of unity are basic tools for the construction of immersions of spaces in standard spaces. In particular, they are used for imbedding manifolds in Euclidean spaces and for the proof of the theorem about the metrizability of each Tikhonov space with a $\sigma$-locally finite base. Moreover, in the theory of manifolds partitions of unity form the basis of methods with the help of which a simultaneous synthesis of local constructions is obtained, after first constructing within the boundaries of individual charts objects with certain desired properties (in particular, for vector or tensor fields). Therefore one of the requirements assumed in the theory of manifolds is the requirement of paracompactness, which is not superfluous since there exist non-paracompact connected Hausdorff spaces, which are locally like $\mathbf R^n$.
In the presence of paracompactness some local properties are synthesized and fulfilled globally. In particular, if a paracompactum is locally metrizable, then it is metrizable; if a Hausdorff space is locally complete in the sense of Čech and paracompact, then it is complete in the sense of Čech. In dimension theory, a number of important relations for paracompacta have been obtained which do not even extend to normal spaces. This is not surprising since one of the basic definitions of dimension — due to Lebesgue and connected with the examination of the multiplicity of open coverings, is plainly related to the concept of local finiteness and this is basic to the definition of paracompactness.
Paracompactness is not inherited by arbitrary subspaces (in which it differs from metrizability), otherwise, for example, all Tikhonov spaces, as subspaces of Hausdorff compacta, would be paracompact. However, each closed subspace of a paracompactum is a paracompactum. An important shortfall of paracompactness is its lack of multiplicativity: The product of two paracompacta need not be a paracompactum. On the other hand, in the class of Hausdorff spaces, the inverse image of a paracompactum under a perfect mapping is a paracompactum, and the image of a paracompactum under a continuous closed mapping is a paracompactum. Lindelöf spaces (cf. Lindelöf space) are, in particular, paracompacta. For the space of all continuous real functions on an arbitrary Tikhonov space, with the topology of pointwise convergence, paracompactness is equivalent to the space being Lindelöf. If a Banach space in the weak topology is topologically generated by some compactum lying within it, then it is paracompact. An important example of paracompacta are the polyhedra underlying CW-complexes.
In the class of paracompacta the metrizability conditions are simplified. In particular, a paracompactum is metrizable if and only if it possesses a base of countable order, i.e. a base such that any decreasing sequence of elements of it containing an arbitrary point $x\in X$ forms a base at that point. There are many paracompactness criteria. In particular, for a Tikhonov space $X$ the following conditions are equivalent: a) $X$ is paracompact; b) any open covering of $X$ can be refined to a locally finite covering; c) any open covering of $X$ can be refined to a $\sigma$-locally finite open covering; and d) any open covering of $X$ can be refined to a conservative closed covering, i.e. to a covering such that the union of any subcollection of it is closed in $X$.
The following criterion is important: A Tikhonov space is paracompact if and only if each open covering $\gamma$ of it has an open star refinement $\lambda$; the latter means that for each point $x\in X$ the union of all elements of $\lambda$ containing $x$ is contained in some element of $\gamma$. The concept of star refinability serves as an expression of the idea of unlimited division of a space, and can be interpreted as the most general set-theoretical form of the triangle axiom.
References
| [1] | J.L. Kelley, "General topology" , Springer (1975) |
| [2] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
| [3] | A.V. Arkhangelskii, "New criteria for paracompactness and metrizability of an arbitrary 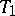 -space" Soviet Math. Dokl. , 2 : 6 (1961) pp. 1367–1370 Dokl. Akad. Nauk SSSR , 141 : 1 (1961) pp. 13–15 -space" Soviet Math. Dokl. , 2 : 6 (1961) pp. 1367–1370 Dokl. Akad. Nauk SSSR , 141 : 1 (1961) pp. 13–15 |
Comments
Stone's theorem mentioned above is due to A.H. Stone (not Marshall Stone).
Conservative collections are also called closure-preserving; star refinements are also called barycentric refinements.
There are a number of variations of the theme of paracompactness. To describe those, a number of concepts of coverings are needed. A family of sets is called disjoint if its elements are mutually disjoint. A $\sigma$-disjoint covering is a countable union of disjoint coverings. A point-finite covering $\gamma$ of a space $X$ is such that each $x\in X$ is contained in only finitely many elements of $\gamma$. A $\sigma$-point-finite covering is a countable union of point-finite ones. A covering $\gamma$ is star-finite, respectively star-countable, if each element of $\gamma$ intersects only finitely many, respectively countably many, others.
A space is called strongly paracompact if each open covering has an open star-finite refinement; it is called weakly paracompact, respectively $\sigma$-metacompact, if each open covering has an open star-finite, respectively $\sigma$-star-finite, refinement. A space is called screened if every open covering has a $\sigma$-disjoint open refinement. A space is hereditarily paracompact if every subspace is paracompact. A space is star-normal or star-paracompact if every open covering has an open star refinement. It is countably paracompact if every open covering has an open locally compact refinement; it is $\tau$-paracompact, where $\tau$ is a cardinal number, if the same holds for open coverings of cardinality $\leq\tau$. For more details and relations of all these variations with each other and other topological properties cf. [2]. Paracompactness itself remains the central notion.
As remarked above, paracompactness is a very natural and useful property. It is therefore most unfortunate that the property is not inherited by subspaces and products. In the case of another concept (than topological space) to capture ideas of near and convergence, the so-called nearness spaces, this drawback disappears; cf. [a1] and Topological structures. For the notion "complete in the sense of Čech" cf. Complete space.
References
| [a1] | G. Preuss, "Theory of topological structures" , Reidel (1988) |
| [a2] | D.K. Burke, "Covering properties" K. Kunen (ed.) J.E. Vaughan (ed.) , Handbook of Set-Theoretic Topology , North-Holland (1984) pp. Chapt. 9; pp. 347–422 |
| [a3] | R. Engelking, "General topology" , Heldermann (1989) |
Paracompact space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Paracompact_space&oldid=15874