Difference between revisions of "Approximation solvability"
(Importing text file) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 91 formulas, 90 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
''A-solvability'' | ''A-solvability'' | ||
| − | Let | + | Let $X$ and $Y$ be Banach spaces (cf. also [[Banach space|Banach space]]), let $T : X \rightarrow Y$ be a, possibly non-linear, mapping (cf. also [[Non-linear operator|Non-linear operator]]) and let $\Gamma = \{ X _ { n } , P _ { n } ; Y _ { n } , Q _ { n } \}$ be an admissible scheme for $( X , Y )$, which, for simplicity, is assumed to be a complete projection scheme, i.e. $\{ X _ { n } \} \subset X$ and $\{ Y _ { n } \} \subset Y$ are finite-dimensional subspaces with $\operatorname { dim } X _ { n } = \operatorname { dim } Y _ { n }$ for each $n$ and $P _ { n } : Y \rightarrow X_n$ and $Q _ { n } : Y \rightarrow X _ { n }$ are linear projections such that $P _ { n } x \rightarrow x$ and $Q _ { n } y \rightarrow y$ for $x \in X$ and $y \in Y$. Clearly, such schemes exist if both $X$ and $Y$ have a Schauder basis (cf. also [[Basis|Basis]]; [[Biorthogonal system|Biorthogonal system]]). Consider the equation |
| − | + | \begin{equation} \tag{a1} T x = f , \quad x \in X , f \in Y. \end{equation} | |
One of the basic problems in [[Functional analysis|functional analysis]] is to "solve" (a1). Here, "solvability" of (a1) can be understood in (at least) two manners: | One of the basic problems in [[Functional analysis|functional analysis]] is to "solve" (a1). Here, "solvability" of (a1) can be understood in (at least) two manners: | ||
| − | A) solvability in which a solution | + | A) solvability in which a solution $x \in X$ of (a1) is somehow established; or |
| − | B) approximation solvability of (a1) (with respect to | + | B) approximation solvability of (a1) (with respect to $\Gamma$), in which a solution $x \in X$ of (a1) is obtained as the limit (or at least, a limit point) of solutions $x _ { n } \in X _ { n }$ of finite-dimensional approximate equations: |
| − | + | \begin{equation} \tag{a2} T _ { n } ( x _ { n } ) = Q _ { n } f, \end{equation} | |
| − | + | \begin{equation*} x _ { n } \in X _ { n } , Q _ { n } f \in Y _ { n } , T _ { n } = ( Q _ { n } T ) | _{X _ { n }} , \end{equation*} | |
| − | with | + | with $T _ { n } : X _ { n } \rightarrow Y _ { n }$ continuous for each $n$. If $x _ { n }$ and $x$ are unique, then (a1) is said to be uniquely A-solvable. |
Although the concepts A) and B) are distinct in their purpose, they are not independent. In fact, sometimes knowledge of A) is essential for B) to take place. | Although the concepts A) and B) are distinct in their purpose, they are not independent. In fact, sometimes knowledge of A) is essential for B) to take place. | ||
| − | If | + | If $X$ and $Y$ are Hilbert spaces (cf. [[Hilbert space|Hilbert space]]), the projections $P_n$ and $Q _ { n }$ are assumed to be orthogonal (cf. [[Orthogonal projector|Orthogonal projector]]). If, for example, $\{ \phi _ { n } \} \subset X$ and $\{ \psi _ { n } \} \subset Y$ are orthogonal bases, then $X _ { n } = \operatorname { span } \{ \phi _ { 1 } , \dots , \phi _ { n } \}$ and $Y _ { n } = \operatorname { span } \{ \psi _ { 1 } , \dots , \psi _ { n } \}$, and $P _ { n } x = \sum _ { i = 1 } ^ { n } ( x , \phi _ { i } ) \phi _ { i }$ and $Q _ { n } y = \sum _ { i = 1 } ^ { n } ( y , \psi _ { i } ) \psi _ { i }$ for $x \in X$, $y \in Y$. In this case, setting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130270/a13027041.png"/>, the coefficients $a _ { 1 } ^ { n } , \ldots , a _ { n } ^ { n }$ are determined by (a2), which reduces to the system |
| − | + | \begin{equation*} ( T ( x _ { n } ) , \psi _ { j } ) = ( f , \psi _ { j } ) , j = 1 , \ldots , n. \end{equation*} | |
==A-proper.== | ==A-proper.== | ||
| − | In studying the A-solvability of (a1) one may ask: For what type of linear or non-linear mapping | + | In studying the A-solvability of (a1) one may ask: For what type of linear or non-linear mapping $T : X \rightarrow Y$ is it possible to show that (a1) is uniquely A-solvable? It turns out that the notion of an A-proper mapping is essential in answering this question. |
| − | A mapping | + | A mapping $T : X \rightarrow Y$ is called A-proper if and only if $T _ { n } : X _ { n } \rightarrow Y _ { n }$ is continuous for each $n$ and such that if $\left\{ x _ { n_j } , : x _ { n_j } \in X _ { n_j } \right\}$ is any bounded sequence satisfying $T _ { n_ j } ( x _ { n_j } ) \rightarrow g$ for some $g \in Y$, then there exist a subsequence $\{ x _ { n_ j } ^ { \prime } \}$ and an $x \in X$ such that $x _ { n_j } ^ { \prime } \rightarrow x$ as $j \rightarrow \infty$ and $T ( x ) = g$, as was first shown in [[#References|[a2]]]. |
| − | It was found (see [[#References|[a1]]]) that there are intimate relationships between (unique) A-solvability and A-properness of | + | It was found (see [[#References|[a1]]]) that there are intimate relationships between (unique) A-solvability and A-properness of $T$, shown by the following results: |
| − | R1) If | + | R1) If $T : X \rightarrow Y$ is a continuous linear mapping, then (a1) is uniquely A-solvable if and only if $T$ is A-proper and one-to-one. This is the best possible result, which includes as a special case all earlier results for the Galerkin or Petrov–Galerkin method (cf. also [[Galerkin method|Galerkin method]]). |
| − | R2) If | + | R2) If $T$ is non-linear and |
| − | + | \begin{equation} \tag{a3} \| T _ { n } ( x ) - T _ { n } ( y ) \| \geq \phi ( \| x - y \| ) \end{equation} | |
| − | for all | + | for all $x , y \in X _ { n }$, $n \geq N_0$, where $\phi$ is a continuous function on $\mathbf{R}$ with $\phi ( 0 ) = 0$, $\phi ( t ) > 0$ for $t > 0$ and $\phi ( t ) \rightarrow \infty$ as $t \rightarrow \infty$, then (a1) is uniquely A-solvable for each $f \in Y$ if and only if $T$ is A-proper and one-to-one. If $T$ is continuous, then R2) holds without the condition that $T$ be one-to-one. The result R2) includes various results for strongly monotone or strongly accretive mappings (cf. also [[Accretive mapping|Accretive mapping]]). If $T$ is a continuous linear mapping, then (a3) reduces to |
| − | + | \begin{equation} \tag{a4} \| T _ { n } ( x ) \| \geq c \| x \| \end{equation} | |
| − | for all | + | for all $x \in X _ { n }$, $n \geq N_0$, and some $c > 0$. If, in addition, the scheme $\Gamma = \{ X _ { n } , P _ { n } ; Y _ { n } , Q _ { n } \}$ is nested, i.e. $X _ { n } \subset X _ { n + 1} $ and $Y _ { n } \subset Y _ { n + 1 }$ for all $n$, and $Q _ { n } ^ { * } w \rightarrow w$ in $Y ^ { * }$ for each $w \in Y ^ { * }$, then $T$ is A-proper and one-to-one if and only if (a4) holds. In particular, by R1), equation (a1) is uniquely A-solvable for each $f \in Y$. Without this extra condition on $\Gamma$, equation (a1) is uniquely A-solvable if (a1) is solvable for each $f \in Y$, or if either $X$ or $Y$ is reflexive (cf. also [[Reflexive space|Reflexive space]]). |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> W.V. Petryshyn, "Approximation-solvability of nonlinear functional and differential equations" , ''Monographs'' , '''171''' , M. Dekker (1993)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> W.V. Petryshyn, "On projectional-solvability and Fredholm alternative for equations involving linear A-proper operators" ''Arch. Rat. Anal.'' , '''30''' (1968) pp. 270–284</td></tr></table> |
Latest revision as of 17:43, 1 July 2020
A-solvability
Let $X$ and $Y$ be Banach spaces (cf. also Banach space), let $T : X \rightarrow Y$ be a, possibly non-linear, mapping (cf. also Non-linear operator) and let $\Gamma = \{ X _ { n } , P _ { n } ; Y _ { n } , Q _ { n } \}$ be an admissible scheme for $( X , Y )$, which, for simplicity, is assumed to be a complete projection scheme, i.e. $\{ X _ { n } \} \subset X$ and $\{ Y _ { n } \} \subset Y$ are finite-dimensional subspaces with $\operatorname { dim } X _ { n } = \operatorname { dim } Y _ { n }$ for each $n$ and $P _ { n } : Y \rightarrow X_n$ and $Q _ { n } : Y \rightarrow X _ { n }$ are linear projections such that $P _ { n } x \rightarrow x$ and $Q _ { n } y \rightarrow y$ for $x \in X$ and $y \in Y$. Clearly, such schemes exist if both $X$ and $Y$ have a Schauder basis (cf. also Basis; Biorthogonal system). Consider the equation
\begin{equation} \tag{a1} T x = f , \quad x \in X , f \in Y. \end{equation}
One of the basic problems in functional analysis is to "solve" (a1). Here, "solvability" of (a1) can be understood in (at least) two manners:
A) solvability in which a solution $x \in X$ of (a1) is somehow established; or
B) approximation solvability of (a1) (with respect to $\Gamma$), in which a solution $x \in X$ of (a1) is obtained as the limit (or at least, a limit point) of solutions $x _ { n } \in X _ { n }$ of finite-dimensional approximate equations:
\begin{equation} \tag{a2} T _ { n } ( x _ { n } ) = Q _ { n } f, \end{equation}
\begin{equation*} x _ { n } \in X _ { n } , Q _ { n } f \in Y _ { n } , T _ { n } = ( Q _ { n } T ) | _{X _ { n }} , \end{equation*}
with $T _ { n } : X _ { n } \rightarrow Y _ { n }$ continuous for each $n$. If $x _ { n }$ and $x$ are unique, then (a1) is said to be uniquely A-solvable.
Although the concepts A) and B) are distinct in their purpose, they are not independent. In fact, sometimes knowledge of A) is essential for B) to take place.
If $X$ and $Y$ are Hilbert spaces (cf. Hilbert space), the projections $P_n$ and $Q _ { n }$ are assumed to be orthogonal (cf. Orthogonal projector). If, for example, $\{ \phi _ { n } \} \subset X$ and $\{ \psi _ { n } \} \subset Y$ are orthogonal bases, then $X _ { n } = \operatorname { span } \{ \phi _ { 1 } , \dots , \phi _ { n } \}$ and $Y _ { n } = \operatorname { span } \{ \psi _ { 1 } , \dots , \psi _ { n } \}$, and $P _ { n } x = \sum _ { i = 1 } ^ { n } ( x , \phi _ { i } ) \phi _ { i }$ and $Q _ { n } y = \sum _ { i = 1 } ^ { n } ( y , \psi _ { i } ) \psi _ { i }$ for $x \in X$, $y \in Y$. In this case, setting 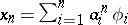 , the coefficients $a _ { 1 } ^ { n } , \ldots , a _ { n } ^ { n }$ are determined by (a2), which reduces to the system
, the coefficients $a _ { 1 } ^ { n } , \ldots , a _ { n } ^ { n }$ are determined by (a2), which reduces to the system
\begin{equation*} ( T ( x _ { n } ) , \psi _ { j } ) = ( f , \psi _ { j } ) , j = 1 , \ldots , n. \end{equation*}
A-proper.
In studying the A-solvability of (a1) one may ask: For what type of linear or non-linear mapping $T : X \rightarrow Y$ is it possible to show that (a1) is uniquely A-solvable? It turns out that the notion of an A-proper mapping is essential in answering this question.
A mapping $T : X \rightarrow Y$ is called A-proper if and only if $T _ { n } : X _ { n } \rightarrow Y _ { n }$ is continuous for each $n$ and such that if $\left\{ x _ { n_j } , : x _ { n_j } \in X _ { n_j } \right\}$ is any bounded sequence satisfying $T _ { n_ j } ( x _ { n_j } ) \rightarrow g$ for some $g \in Y$, then there exist a subsequence $\{ x _ { n_ j } ^ { \prime } \}$ and an $x \in X$ such that $x _ { n_j } ^ { \prime } \rightarrow x$ as $j \rightarrow \infty$ and $T ( x ) = g$, as was first shown in [a2].
It was found (see [a1]) that there are intimate relationships between (unique) A-solvability and A-properness of $T$, shown by the following results:
R1) If $T : X \rightarrow Y$ is a continuous linear mapping, then (a1) is uniquely A-solvable if and only if $T$ is A-proper and one-to-one. This is the best possible result, which includes as a special case all earlier results for the Galerkin or Petrov–Galerkin method (cf. also Galerkin method).
R2) If $T$ is non-linear and
\begin{equation} \tag{a3} \| T _ { n } ( x ) - T _ { n } ( y ) \| \geq \phi ( \| x - y \| ) \end{equation}
for all $x , y \in X _ { n }$, $n \geq N_0$, where $\phi$ is a continuous function on $\mathbf{R}$ with $\phi ( 0 ) = 0$, $\phi ( t ) > 0$ for $t > 0$ and $\phi ( t ) \rightarrow \infty$ as $t \rightarrow \infty$, then (a1) is uniquely A-solvable for each $f \in Y$ if and only if $T$ is A-proper and one-to-one. If $T$ is continuous, then R2) holds without the condition that $T$ be one-to-one. The result R2) includes various results for strongly monotone or strongly accretive mappings (cf. also Accretive mapping). If $T$ is a continuous linear mapping, then (a3) reduces to
\begin{equation} \tag{a4} \| T _ { n } ( x ) \| \geq c \| x \| \end{equation}
for all $x \in X _ { n }$, $n \geq N_0$, and some $c > 0$. If, in addition, the scheme $\Gamma = \{ X _ { n } , P _ { n } ; Y _ { n } , Q _ { n } \}$ is nested, i.e. $X _ { n } \subset X _ { n + 1} $ and $Y _ { n } \subset Y _ { n + 1 }$ for all $n$, and $Q _ { n } ^ { * } w \rightarrow w$ in $Y ^ { * }$ for each $w \in Y ^ { * }$, then $T$ is A-proper and one-to-one if and only if (a4) holds. In particular, by R1), equation (a1) is uniquely A-solvable for each $f \in Y$. Without this extra condition on $\Gamma$, equation (a1) is uniquely A-solvable if (a1) is solvable for each $f \in Y$, or if either $X$ or $Y$ is reflexive (cf. also Reflexive space).
References
| [a1] | W.V. Petryshyn, "Approximation-solvability of nonlinear functional and differential equations" , Monographs , 171 , M. Dekker (1993) |
| [a2] | W.V. Petryshyn, "On projectional-solvability and Fredholm alternative for equations involving linear A-proper operators" Arch. Rat. Anal. , 30 (1968) pp. 270–284 |
Approximation solvability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximation_solvability&oldid=15238