Difference between revisions of "Strophoid"
From Encyclopedia of Mathematics
(Importing text file) |
(gather refs) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A third-order plane algebraic curve whose equation takes the form | A third-order plane algebraic curve whose equation takes the form | ||
| − | + | $$y^2=x^2\frac{d+x}{d-x}$$ | |
in Cartesian coordinates, and | in Cartesian coordinates, and | ||
| − | + | $$\rho=-d\frac{\cos2\phi}{\cos\phi}$$ | |
| − | in polar coordinates. The coordinate origin is a node with tangents | + | in polar coordinates. The coordinate origin is a node with tangents $y=\pm x$ (see Fig.). The asymptote is $x=d$. The area of the loop is |
| − | + | $$S=2d^2-\frac{1}{2\pi d^2}.$$ | |
The area between the curve and the asymptote is | The area between the curve and the asymptote is | ||
| − | + | $$S_2=2d^2+\frac{1}{2\pi d^2}.$$ | |
A strophoid is related to the so-called cusps (cf. [[Cusp(2)|Cusp]]). | A strophoid is related to the so-called cusps (cf. [[Cusp(2)|Cusp]]). | ||
| Line 22: | Line 23: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> F. Gomes Teixeira, "Traité des courbes" , '''1–3''' , Chelsea, reprint (1971)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.D. Lawrence, "A catalog of special planar curves" , Dover, reprint (1972)</TD></TR> | ||
| + | </table> | ||
| + | [[Category:Geometry]] | ||
| − | + | {{OldImage}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 14:02, 9 April 2023
A third-order plane algebraic curve whose equation takes the form
$$y^2=x^2\frac{d+x}{d-x}$$
in Cartesian coordinates, and
$$\rho=-d\frac{\cos2\phi}{\cos\phi}$$
in polar coordinates. The coordinate origin is a node with tangents $y=\pm x$ (see Fig.). The asymptote is $x=d$. The area of the loop is
$$S=2d^2-\frac{1}{2\pi d^2}.$$
The area between the curve and the asymptote is
$$S_2=2d^2+\frac{1}{2\pi d^2}.$$
A strophoid is related to the so-called cusps (cf. Cusp).
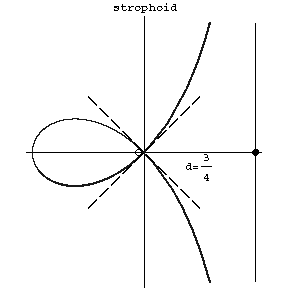
Figure: s090630a
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [2] | A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian) |
| [a1] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
| [a2] | J.D. Lawrence, "A catalog of special planar curves" , Dover, reprint (1972) |
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
How to Cite This Entry:
Strophoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strophoid&oldid=15202
Strophoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strophoid&oldid=15202
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article