Difference between revisions of "Hypergeometric equation"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | h0484401.png | ||
| + | $#A+1 = 37 n = 2 | ||
| + | $#C+1 = 37 : ~/encyclopedia/old_files/data/H048/H.0408440 Hypergeometric equation, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''Gauss equation'' | ''Gauss equation'' | ||
An ordinary second-order linear differential equation | An ordinary second-order linear differential equation | ||
| − | + | $$ \tag{1 } | |
| + | z ( z - 1) w ^ {\prime\prime} + | ||
| + | [( \alpha + \beta + 1) z - \gamma ] | ||
| + | w ^ \prime + \alpha \beta w = 0, | ||
| + | $$ | ||
| − | + | $$ | |
| + | \alpha , \beta , \gamma = \textrm{ const }, | ||
| + | $$ | ||
or, in self-adjoint form, | or, in self-adjoint form, | ||
| − | + | $$ | |
| + | [ z ^ \gamma ( z - 1) ^ {\alpha + \beta + 1 - \gamma } | ||
| + | w ^ \prime ] ^ \prime + \alpha \beta z ^ {\gamma - 1 } | ||
| + | ( z - 1) ^ {\alpha + \beta - \gamma } w = 0. | ||
| + | $$ | ||
| − | The variables | + | The variables $ z, w $ |
| + | and the parameters $ \alpha , \beta , \gamma $ | ||
| + | assume, in the general case, complex values. After substituting | ||
| − | + | $$ | |
| + | w = z ^ {- \gamma / 2 } | ||
| + | ( z - 1) ^ {( \gamma - \alpha - \beta - 1)/2 } u | ||
| + | $$ | ||
the reduced form of equation (1) is obtained: | the reduced form of equation (1) is obtained: | ||
| − | + | $$ \tag{2 } | |
| + | u ^ {\prime\prime} + \left [ | ||
| + | \frac{1 - \lambda ^ {2} }{4z ^ {2} } | ||
| + | + | ||
| + | |||
| + | \frac{1 - \gamma ^ {2} }{4 ( z - 1) ^ {2} } | ||
| + | - | ||
| + | |||
| + | \frac{1 - \lambda ^ {2} + \mu ^ {2} - \gamma ^ {2} }{4z ( z - 1) } | ||
| + | \right ] u = 0, | ||
| + | $$ | ||
| − | where | + | where $ \lambda = 1 - \gamma $, |
| + | $ \mu = \alpha - \beta $, | ||
| + | and $ \nu = \gamma - \alpha - \beta $. | ||
Equation (1) was studied in detail by C.F. Gauss | Equation (1) was studied in detail by C.F. Gauss | ||
| Line 25: | Line 64: | ||
in connection with his theory of the [[Hypergeometric series|hypergeometric series]], but had been considered (together with its solution) by L. Euler at an even earlier date. | in connection with his theory of the [[Hypergeometric series|hypergeometric series]], but had been considered (together with its solution) by L. Euler at an even earlier date. | ||
| − | Solutions of equation (1) are expressed by way of the [[Hypergeometric function|hypergeometric function]] | + | Solutions of equation (1) are expressed by way of the [[Hypergeometric function|hypergeometric function]] $ F( \alpha , \beta ; \gamma ; z ) $. |
| + | If $ \gamma $ | ||
| + | is not an integer, the general solution of (1) may be written as | ||
| − | + | $$ \tag{3 } | |
| + | w = C _ {1} F ( \alpha , \beta ; \gamma ; z) + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | C _ {2} z ^ {1 - \gamma } F ( \alpha - \gamma | ||
| + | + 1, \beta - \gamma + 1; 2 - \gamma ; z), | ||
| + | $$ | ||
| − | where | + | where $ C _ {1} $ |
| + | and $ C _ {2} $ | ||
| + | are arbitrary constants. The representation (3) is valid in the complex $ z $- | ||
| + | plane with slits $ ( - \infty , 0) $ | ||
| + | and $ ( 1, \infty ) $. | ||
| + | In particular, in the real case (3) yields the general solution of (1) in the interval $ 0 < z < 1 $. | ||
| + | For integral values of $ \gamma $ | ||
| + | the general solution is more complicated (the individual terms may contain logarithms). | ||
| − | Functions other than those shown in (3) may also be selected as a [[Fundamental system of solutions|fundamental system of solutions]] of equation (1). For instance, if | + | Functions other than those shown in (3) may also be selected as a [[Fundamental system of solutions|fundamental system of solutions]] of equation (1). For instance, if $ \alpha - \beta $ |
| + | is not an integer, then | ||
| − | + | $$ | |
| + | w = C _ {1} (- z) ^ {- \alpha } F ( \alpha , \alpha - \gamma + 1; \ | ||
| + | \alpha - \beta + 1; z ^ {- 1 } ) + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | C _ {2} (- z) ^ {- \beta } F ( \beta - \gamma + | ||
| + | 1, \beta ; \beta - \alpha + 1; z ^ {- 1 } ) | ||
| + | $$ | ||
| − | is the general solution of (1) in the complex plane with slit | + | is the general solution of (1) in the complex plane with slit $ ( 0, \infty ) $[[#References|[2]]], [[#References|[3]]]. |
| − | The Gauss equations include, as particular cases, a number of differential equations encountered in applications; many ordinary linear second-order differential equations are reduced to (1) by transforming the unknown function and the independent variable [[#References|[4]]]. The [[Confluent hypergeometric equation|confluent hypergeometric equation]], which is close to equation (1), is particularly important. The ratio | + | The Gauss equations include, as particular cases, a number of differential equations encountered in applications; many ordinary linear second-order differential equations are reduced to (1) by transforming the unknown function and the independent variable [[#References|[4]]]. The [[Confluent hypergeometric equation|confluent hypergeometric equation]], which is close to equation (1), is particularly important. The ratio $ s( z) $ |
| + | of two linearly independent solutions of equation (2) satisfies the [[Schwarz equation|Schwarz equation]], which is closely connected with the problem of conformal mapping a semi-plane onto a triangle bounded by three peripheral arcs. The study of the inverse function $ z( s) $ | ||
| + | leads to the concept of an [[Automorphic function|automorphic function]] [[#References|[5]]]. | ||
| − | There exist linear equations of higher orders whose solutions display properties similar to those of hypergeometric functions: The solution of the following equation of order | + | There exist linear equations of higher orders whose solutions display properties similar to those of hypergeometric functions: The solution of the following equation of order $ q+ 1 $, |
| − | + | $$ | |
| + | \left [ z { | ||
| + | \frac{d}{dz} | ||
| + | } | ||
| + | \prod _ {j = 1 } ^ { q } | ||
| + | \left ( z { | ||
| + | \frac{d}{dz} | ||
| + | } + \gamma _ {j} - 1 \right ) - | ||
| + | z \prod _ {i = 1 } ^ { p } | ||
| + | \left ( z { | ||
| + | \frac{d}{dz} | ||
| + | } + \alpha _ {i} \right ) \right ] | ||
| + | w = 0, | ||
| + | $$ | ||
| − | is the generalized hypergeometric function | + | is the generalized hypergeometric function $ {} _ {p} F _ {q} ( \alpha _ {i} ; \gamma _ {j} ; z) $ |
| + | with $ p+ q $ | ||
| + | parameters. In particular, the generalized hypergeometric equation of the third order, the solution of which is $ {} _ {3} F _ {2} ( \alpha _ {1} , \alpha _ {2} , \alpha _ {3} ; \gamma _ {1} , \gamma _ {2} ; z ) $, | ||
| + | may be represented as | ||
| − | + | $$ | |
| + | z ^ {2} ( 1 - z) w ^ {\prime\prime\prime} + | ||
| + | [ 1 + \gamma _ {1} + \gamma _ {2} - | ||
| + | ( 3 + \alpha _ {1} + \alpha _ {2} + | ||
| + | \alpha _ {3} ) z] zw ^ {\prime\prime} + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | [ \gamma _ {1} \gamma _ {2} - ( 1 + \alpha _ {1} + | ||
| + | \alpha _ {2} + \alpha _ {3} + \alpha _ {1} \alpha _ {2} + \alpha _ {2} \alpha _ {3} + \alpha _ {3} \alpha _ {1} ) z] w ^ \prime + | ||
| + | $$ | ||
| − | + | $$ | |
| + | - \alpha _ {1} \alpha _ {2} \alpha _ {3} w = 0. | ||
| + | $$ | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1a]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1a]</TD> <TD valign="top"> C.F. Gauss, "Disquisitiones generales circa seriem infinitam <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048440/h04844036.png" />" ''Comm. Soc. Regia Sci. Göttingen Rec.'' , '''2''' (1812)</TD></TR><TR><TD valign="top">[1b]</TD> <TD valign="top"> C.F. Gauss, "Disquisitiones generales circa seriem infinitam <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048440/h04844037.png" />" , ''Werke'' , '''3''' , K. Gesellschaft Wissenschaft. Göttingen (1876)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Krazer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960) {{MR|124531}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Bateman (ed.) A. Erdélyi (ed.) , ''Higher transcendental functions'' , '''1–3''' , McGraw-Hill (1953–1955) {{MR|0698781}} {{MR|0698780}} {{MR|0698779}} {{MR|0355126}} {{MR|0344526}} {{MR|0243127}} {{MR|0201683}} {{MR|0066496}} {{MR|1528832}} {{MR|0058756}} {{ZBL|0157.11901}} {{ZBL|0143.29202}} {{ZBL|0146.09301}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , '''1. Gewöhnliche Differentialgleichungen''' , Chelsea, reprint (1971)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) {{MR|0100119}} {{ZBL|}} </TD></TR></table> |
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The hypergeometric equation is a differential equation with three regular singular points (cf. [[Regular singular point|Regular singular point]]) at 0, 1 and | + | The hypergeometric equation is a differential equation with three regular singular points (cf. [[Regular singular point|Regular singular point]]) at 0, 1 and $ \infty $ |
| + | such that both at 0 and 1 one of the exponents equals 0. So it is a special case of the [[Riemann differential equation|Riemann differential equation]]. The hypergeometric equation has been generalized to a system of partial differential equations with regular singularities such that the Appell or Lauricella hypergeometric function in several variables is a solution, cf. [[#References|[a1]]]. In [[#References|[a2]]], [[#References|[a3]]] a study is made of a second-order partial differential equation associated with a root system, which generalizes the case of the root system $ BC _ {1} $ | ||
| + | for the ordinary hypergeometric equation. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Appell, M.J. Kampé de Fériet, "Fonctions hypergéométriques et hypersphériques: Polynômes d'Hermite" , Gauthier-Villars (1926) {{MR|}} {{ZBL|52.0361.13}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G.J. Heckman, E.M. Opdam, "Root systems and hypergeometric functions I" ''Compositio Math.'' , '''64''' (1987) pp. 329–352 {{MR|0918416}} {{MR|0918417}} {{ZBL|0656.17006}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.J. Heckman, "Root systems and hypergeometric functions II" ''Compositio Math.'' , '''64''' (1987) pp. 353–373 {{MR|0918416}} {{MR|0918417}} {{ZBL|0656.17007}} </TD></TR></table> |
Latest revision as of 22:11, 5 June 2020
Gauss equation
An ordinary second-order linear differential equation
$$ \tag{1 } z ( z - 1) w ^ {\prime\prime} + [( \alpha + \beta + 1) z - \gamma ] w ^ \prime + \alpha \beta w = 0, $$
$$ \alpha , \beta , \gamma = \textrm{ const }, $$
or, in self-adjoint form,
$$ [ z ^ \gamma ( z - 1) ^ {\alpha + \beta + 1 - \gamma } w ^ \prime ] ^ \prime + \alpha \beta z ^ {\gamma - 1 } ( z - 1) ^ {\alpha + \beta - \gamma } w = 0. $$
The variables $ z, w $ and the parameters $ \alpha , \beta , \gamma $ assume, in the general case, complex values. After substituting
$$ w = z ^ {- \gamma / 2 } ( z - 1) ^ {( \gamma - \alpha - \beta - 1)/2 } u $$
the reduced form of equation (1) is obtained:
$$ \tag{2 } u ^ {\prime\prime} + \left [ \frac{1 - \lambda ^ {2} }{4z ^ {2} } + \frac{1 - \gamma ^ {2} }{4 ( z - 1) ^ {2} } - \frac{1 - \lambda ^ {2} + \mu ^ {2} - \gamma ^ {2} }{4z ( z - 1) } \right ] u = 0, $$
where $ \lambda = 1 - \gamma $, $ \mu = \alpha - \beta $, and $ \nu = \gamma - \alpha - \beta $.
Equation (1) was studied in detail by C.F. Gauss
in connection with his theory of the hypergeometric series, but had been considered (together with its solution) by L. Euler at an even earlier date.
Solutions of equation (1) are expressed by way of the hypergeometric function $ F( \alpha , \beta ; \gamma ; z ) $. If $ \gamma $ is not an integer, the general solution of (1) may be written as
$$ \tag{3 } w = C _ {1} F ( \alpha , \beta ; \gamma ; z) + $$
$$ + C _ {2} z ^ {1 - \gamma } F ( \alpha - \gamma + 1, \beta - \gamma + 1; 2 - \gamma ; z), $$
where $ C _ {1} $ and $ C _ {2} $ are arbitrary constants. The representation (3) is valid in the complex $ z $- plane with slits $ ( - \infty , 0) $ and $ ( 1, \infty ) $. In particular, in the real case (3) yields the general solution of (1) in the interval $ 0 < z < 1 $. For integral values of $ \gamma $ the general solution is more complicated (the individual terms may contain logarithms).
Functions other than those shown in (3) may also be selected as a fundamental system of solutions of equation (1). For instance, if $ \alpha - \beta $ is not an integer, then
$$ w = C _ {1} (- z) ^ {- \alpha } F ( \alpha , \alpha - \gamma + 1; \ \alpha - \beta + 1; z ^ {- 1 } ) + $$
$$ + C _ {2} (- z) ^ {- \beta } F ( \beta - \gamma + 1, \beta ; \beta - \alpha + 1; z ^ {- 1 } ) $$
is the general solution of (1) in the complex plane with slit $ ( 0, \infty ) $[2], [3].
The Gauss equations include, as particular cases, a number of differential equations encountered in applications; many ordinary linear second-order differential equations are reduced to (1) by transforming the unknown function and the independent variable [4]. The confluent hypergeometric equation, which is close to equation (1), is particularly important. The ratio $ s( z) $ of two linearly independent solutions of equation (2) satisfies the Schwarz equation, which is closely connected with the problem of conformal mapping a semi-plane onto a triangle bounded by three peripheral arcs. The study of the inverse function $ z( s) $ leads to the concept of an automorphic function [5].
There exist linear equations of higher orders whose solutions display properties similar to those of hypergeometric functions: The solution of the following equation of order $ q+ 1 $,
$$ \left [ z { \frac{d}{dz} } \prod _ {j = 1 } ^ { q } \left ( z { \frac{d}{dz} } + \gamma _ {j} - 1 \right ) - z \prod _ {i = 1 } ^ { p } \left ( z { \frac{d}{dz} } + \alpha _ {i} \right ) \right ] w = 0, $$
is the generalized hypergeometric function $ {} _ {p} F _ {q} ( \alpha _ {i} ; \gamma _ {j} ; z) $ with $ p+ q $ parameters. In particular, the generalized hypergeometric equation of the third order, the solution of which is $ {} _ {3} F _ {2} ( \alpha _ {1} , \alpha _ {2} , \alpha _ {3} ; \gamma _ {1} , \gamma _ {2} ; z ) $, may be represented as
$$ z ^ {2} ( 1 - z) w ^ {\prime\prime\prime} + [ 1 + \gamma _ {1} + \gamma _ {2} - ( 3 + \alpha _ {1} + \alpha _ {2} + \alpha _ {3} ) z] zw ^ {\prime\prime} + $$
$$ + [ \gamma _ {1} \gamma _ {2} - ( 1 + \alpha _ {1} + \alpha _ {2} + \alpha _ {3} + \alpha _ {1} \alpha _ {2} + \alpha _ {2} \alpha _ {3} + \alpha _ {3} \alpha _ {1} ) z] w ^ \prime + $$
$$ - \alpha _ {1} \alpha _ {2} \alpha _ {3} w = 0. $$
References
| [1a] | C.F. Gauss, "Disquisitiones generales circa seriem infinitam 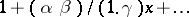 " Comm. Soc. Regia Sci. Göttingen Rec. , 2 (1812) " Comm. Soc. Regia Sci. Göttingen Rec. , 2 (1812) |
| [1b] | C.F. Gauss, "Disquisitiones generales circa seriem infinitam 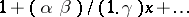 " , Werke , 3 , K. Gesellschaft Wissenschaft. Göttingen (1876) " , Werke , 3 , K. Gesellschaft Wissenschaft. Göttingen (1876) |
| [2] | A. Krazer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960) MR124531 |
| [3] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1–3 , McGraw-Hill (1953–1955) MR0698781 MR0698780 MR0698779 MR0355126 MR0344526 MR0243127 MR0201683 MR0066496 MR1528832 MR0058756 Zbl 0157.11901 Zbl 0143.29202 Zbl 0146.09301 |
| [4] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971) |
| [5] | V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) MR0100119 |
Comments
The hypergeometric equation is a differential equation with three regular singular points (cf. Regular singular point) at 0, 1 and $ \infty $ such that both at 0 and 1 one of the exponents equals 0. So it is a special case of the Riemann differential equation. The hypergeometric equation has been generalized to a system of partial differential equations with regular singularities such that the Appell or Lauricella hypergeometric function in several variables is a solution, cf. [a1]. In [a2], [a3] a study is made of a second-order partial differential equation associated with a root system, which generalizes the case of the root system $ BC _ {1} $ for the ordinary hypergeometric equation.
References
| [a1] | P. Appell, M.J. Kampé de Fériet, "Fonctions hypergéométriques et hypersphériques: Polynômes d'Hermite" , Gauthier-Villars (1926) Zbl 52.0361.13 |
| [a2] | G.J. Heckman, E.M. Opdam, "Root systems and hypergeometric functions I" Compositio Math. , 64 (1987) pp. 329–352 MR0918416 MR0918417 Zbl 0656.17006 |
| [a3] | G.J. Heckman, "Root systems and hypergeometric functions II" Compositio Math. , 64 (1987) pp. 353–373 MR0918416 MR0918417 Zbl 0656.17007 |
Hypergeometric equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hypergeometric_equation&oldid=14414