|
|
| (2 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b1204402.png" />-local structure of a [[Finite group|finite group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b1204403.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b1204404.png" /> is a [[Prime number|prime number]], is the collection of non-trivial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b1204405.png" />-subgroups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b1204406.png" /> (cf. also [[P-group|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b1204407.png" />-group]]), together with their normalizers and centralizers (cf. also [[Centralizer|Centralizer]]; [[Normalizer of a subset|Normalizer of a subset]]). One of the principal goals of representation theory (cf. also [[Representation of a group|Representation of a group]]) is to find rules relating representations and characters to the various <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b1204408.png" />-local structures of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b1204409.png" />. If a prime number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044010.png" /> is fixed, representations over fields (cf. also [[Field|Field]]) of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044011.png" />, and values of irreducible complex characters on elements of order divisible by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044012.png" />, are controlled to a considerable extent by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044013.png" />-local structure. Brauer's three main theorems on blocks are the oldest and most important tools for investigating this phenomenon. (See also [[Brauer second main theorem|Brauer second main theorem]]; [[Brauer third main theorem|Brauer third main theorem]].)
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | The first step is the partition of indecomposable representations and irreducible characters into blocks. Fix a prime number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044014.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044015.png" /> be a complete discrete [[Valuation|valuation]] ring of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044016.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044017.png" /> in its radical <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044018.png" /> (cf. also [[Radical of rings and algebras|Radical of rings and algebras]]), let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044019.png" /> be its field of fractions, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044020.png" /> be the residue field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044021.png" />. Assume, in addition, that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044022.png" /> contains an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044023.png" />th root of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044024.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044025.png" /> is the least common multiple of the orders of the elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044026.png" />. The [[Group algebra|group algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044027.png" /> has a unique decomposition as a direct sum of indecomposable two-sided ideals,
| + | Out of 125 formulas, 122 were replaced by TEX code.--> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044028.png" /></td> </tr></table>
| + | {{TEX|semi-auto}}{{TEX|part}} |
| | + | The $p$-local structure of a [[Finite group|finite group]] $G$, where $p$ is a [[Prime number|prime number]], is the collection of non-trivial $p$-subgroups of $G$ (cf. also [[P-group|$p$-group]]), together with their normalizers and centralizers (cf. also [[Centralizer|Centralizer]]; [[Normalizer of a subset|Normalizer of a subset]]). One of the principal goals of representation theory (cf. also [[Representation of a group|Representation of a group]]) is to find rules relating representations and characters to the various $p$-local structures of $G$. If a prime number $p$ is fixed, representations over fields (cf. also [[Field|Field]]) of characteristic $p$, and values of irreducible complex characters on elements of order divisible by $p$, are controlled to a considerable extent by the $p$-local structure. Brauer's three main theorems on blocks are the oldest and most important tools for investigating this phenomenon. (See also [[Brauer second main theorem|Brauer second main theorem]]; [[Brauer third main theorem|Brauer third main theorem]].) |
| | | | |
| − | The ideals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044029.png" /> are called the blocks of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044030.png" />. Applying to this decomposition the natural mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044031.png" /> (i.e. reducing coefficients modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044032.png" />), one obtains the unique decomposition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044033.png" /> as a direct sum of indecomposable two-sided ideals. Any indecomposable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044034.png" />-free <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044035.png" />-module, or any indecomposable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044036.png" />-module, is annihilated by all blocks except one, and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044037.png" /> is an irreducible <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044038.png" />-character of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044039.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044040.png" /> for all but one <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044041.png" />. Thus, to each block belong a category of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044042.png" />-free <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044043.png" />-modules, a category of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044044.png" />-modules, and a set of irreducible <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044045.png" />-characters. The word "block" is sometimes used to refer to the corresponding categories or the corresponding set of characters, rather than to the ideal. | + | The first step is the partition of indecomposable representations and irreducible characters into blocks. Fix a prime number $p$. Let $R$ be a complete discrete [[Valuation|valuation]] ring of characteristic $0$ with $p$ in its radical $J ( R )$ (cf. also [[Radical of rings and algebras|Radical of rings and algebras]]), let $K$ be its field of fractions, and let $k$ be the residue field $R / J ( R )$. Assume, in addition, that $K$ contains an $e$th root of $1$, where $e$ is the least common multiple of the orders of the elements of $G$. The [[Group algebra|group algebra]] $R G$ has a unique decomposition as a direct sum of indecomposable two-sided ideals, |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044047.png" /> be the subfield of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044048.png" /> consisting of all elements that are algebraic over the prime subfield (cf. also [[Algebraic number|Algebraic number]]). The values on elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044049.png" /> of any irreducible <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044050.png" />-character are in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044051.png" />. If an imbedding of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044052.png" /> in the complex numbers is chosen, the irreducible <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044053.png" />-characters of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044054.png" /> can be identified with the irreducible complex characters of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044055.png" />. Thus, the irreducible complex characters are partitioned into blocks. This partition is independent of the choice of the imbedding. When it is not clear from the context which prime number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044056.png" /> is intended, one refers to a partition of the irreducible complex characters into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044059.png" />-blocks.
| + | \begin{equation*} R G = B _ { 1 } \bigoplus \ldots \bigoplus B _ { n }. \end{equation*} |
| | | | |
| − | To each block is associated a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044060.png" />-conjugacy class of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044061.png" />-subgroups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044062.png" />, called its defect groups (cf. also [[Defect group of a block|Defect group of a block]]), which substantially control its representation theory. They are defined as follows. Fix a block <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044063.png" />. For any [[Subgroup|subgroup]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044064.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044065.png" />, let
| + | The ideals $B _ { i }$ are called the blocks of $R G$. Applying to this decomposition the natural mapping $R G \rightarrow k G$ (i.e. reducing coefficients modulo $J ( R )$), one obtains the unique decomposition of $k G$ as a direct sum of indecomposable two-sided ideals. Any indecomposable $R$-free $R G$-module, or any indecomposable $k G$-module, is annihilated by all blocks except one, and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044037.png"/> is an irreducible $K$-character of $G$, then $\chi ( B _ { i } ) = 0$ for all but one $i$. Thus, to each block belong a category of $R$-free $R G$-modules, a category of $k G$-modules, and a set of irreducible $K$-characters. The word "block" is sometimes used to refer to the corresponding categories or the corresponding set of characters, rather than to the ideal. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044066.png" /></td> </tr></table>
| + | Let $L$ be the subfield of $K$ consisting of all elements that are algebraic over the prime subfield (cf. also [[Algebraic number|Algebraic number]]). The values on elements of $G$ of any irreducible $K$-character are in $L$. If an imbedding of $L$ in the complex numbers is chosen, the irreducible $K$-characters of $G$ can be identified with the irreducible complex characters of $G$. Thus, the irreducible complex characters are partitioned into blocks. This partition is independent of the choice of the imbedding. When it is not clear from the context which prime number $p$ is intended, one refers to a partition of the irreducible complex characters into $p$-blocks. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044067.png" /> be given by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044068.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044069.png" /> is a set of representatives for the right cosets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044070.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044071.png" />. The set of subgroups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044072.png" /> minimal such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044073.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044074.png" />-conjugacy class of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044075.png" />-subgroups; they are called the defect groups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044076.png" />. If a block has defect group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044077.png" />, then it is isomorphic as an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044078.png" />-algebra to a full [[Matrix algebra|matrix algebra]] with entries in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044079.png" />, and it is associated to just a single irreducible character, a single indecomposable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044080.png" />-free <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044081.png" />-module, and a single indecomposable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044082.png" />-module. Blocks with cyclic defect group are very well understood, due to work of E.C. Dade (see [[#References|[a5]]], Chap. VII). The process of understanding blocks with more complicated defect groups is still far from complete (as of 1998). For example, R. Brauer has conjectured that the number of irreducible characters belonging to a block with defect group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044083.png" /> is less than or equal to the order of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044084.png" />. See also [[Brauer height-zero conjecture|Brauer height-zero conjecture]].
| + | To each block is associated a $G$-conjugacy class of $p$-subgroups of $G$, called its defect groups (cf. also [[Defect group of a block|Defect group of a block]]), which substantially control its representation theory. They are defined as follows. Fix a block $B$. For any [[Subgroup|subgroup]] $H$ of $G$, let |
| | | | |
| − | The Brauer correspondence is a tool for relating blocks of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044085.png" /> to blocks of subgroups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044086.png" />; it is defined as follows. The algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044087.png" /> is a right module over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044088.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044089.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044090.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044091.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044092.png" />. The decomposition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044093.png" /> into blocks is also a decomposition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044094.png" /> as a direct sum of indecomposable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044095.png" />-modules. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044096.png" /> be a subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044097.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044098.png" /> be a block of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044099.png" />. If there is a unique block <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440100.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440101.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440102.png" /> isomorphic as an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440103.png" />-module to a direct summand of the restriction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440104.png" />, then one says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440105.png" /> is defined and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440106.png" />. The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440107.png" /> is called the Brauer correspondence. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440108.png" /> be a defect group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440109.png" />. Assume that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440110.png" />; then in any decomposition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440111.png" /> as a direct sum of indecomposable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440112.png" />-modules there is a unique module isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440113.png" />; so certainly <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440114.png" /> is defined. Most of the important applications of the Brauer correspondence arise in this way.
| + | \begin{equation*} B ^ { H } = \{ a \in B : h ^ { - 1 } a h =a \ \text {for all } h \in H \}. \end{equation*} |
| | | | |
| − | Brauer's original definition of this correspondence in terms of central characters (see [[#References|[a5]]], Chap. III) yields a mapping that has a slightly different domain of definition from the mapping described here. The mappings agree on the intersection of their domains, and both are defined in the important case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440115.png" />.
| + | Let $T _ { H } ^ { G } : B ^ { H } \rightarrow B ^ { G }$ be given by $T _ { H } ^ { G } ( a ) = \sum _ { j } g _ { j } ^ { - 1 } a g_j$, where $\{ g_j\}$ is a set of representatives for the right cosets of $H$ in $G$. The set of subgroups $H$ minimal such that $B ^ { G } = T _ { H } ^ { G } ( B ^ { H } )$ is a $G$-conjugacy class of $p$-subgroups; they are called the defect groups of $B$. If a block has defect group $1$, then it is isomorphic as an $R$-algebra to a full [[Matrix algebra|matrix algebra]] with entries in $R$, and it is associated to just a single irreducible character, a single indecomposable $R$-free $R G$-module, and a single indecomposable $k G$-module. Blocks with cyclic defect group are very well understood, due to work of E.C. Dade (see [[#References|[a5]]], Chap. VII). The process of understanding blocks with more complicated defect groups is still far from complete (as of 1998). For example, R. Brauer has conjectured that the number of irreducible characters belonging to a block with defect group $D$ is less than or equal to the order of $D$. See also [[Brauer height-zero conjecture|Brauer height-zero conjecture]]. |
| | | | |
| − | Brauer's first main theorem says that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440116.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440117.png" />-subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440118.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440119.png" /> is a subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440120.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440121.png" />, then the Brauer correspondence gives a bijection between the blocks of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440122.png" /> with defect group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440123.png" /> and the blocks of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440124.png" /> with defect group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440125.png" />. Thus, the number of blocks with non-trivial defect group is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440126.png" />-locally determined. | + | The Brauer correspondence is a tool for relating blocks of $G$ to blocks of subgroups of $G$; it is defined as follows. The algebra $R G$ is a right module over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044088.png"/>, with $a ( g h ) = g ^ { - 1 } a h$ for all $g \in G$, $h \in G$, and $a \in R G$. The decomposition of $R G$ into blocks is also a decomposition of $R G$ as a direct sum of indecomposable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b12044095.png"/>-modules. Let $H$ be a subgroup of $G$ and let $b$ be a block of $R H$. If there is a unique block $B$ of $G$ with $b$ isomorphic as an $R [ H \times H]$-module to a direct summand of the restriction $B _ { R [ H \times H ]}$, then one says that $b ^ { G }$ is defined and $B = b ^ { G }$. The mapping $b \mapsto b ^ { G }$ is called the Brauer correspondence. Let $D$ be a defect group of $b$. Assume that $C _ { G } ( D ) \subseteq H$; then in any decomposition of $R G$ as a direct sum of indecomposable $R [ H \times H]$-modules there is a unique module isomorphic to $b$; so certainly $b ^ { G }$ is defined. Most of the important applications of the Brauer correspondence arise in this way. |
| | | | |
| − | There is a close relationship between a block of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440127.png" /> with defect group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440128.png" /> and the corresponding block of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120440/b120440129.png" />; however, the investigation of this relationship is far from complete. See, for example, [[McKay–Alperin conjecture|McKay–Alperin conjecture]], the Broué conjecture in [[#References|[a3]]], or the many consequences of the Alperin weight conjecture in [[#References|[a2]]]. | + | Brauer's original definition of this correspondence in terms of central characters (see [[#References|[a5]]], Chap. III) yields a mapping that has a slightly different domain of definition from the mapping described here. The mappings agree on the intersection of their domains, and both are defined in the important case when $C _ { G } ( D ) \subseteq H$. |
| | + | |
| | + | Brauer's first main theorem says that if $D$ is a $p$-subgroup of $G$ and $H$ is a subgroup of $G$ with $N _ { G } ( D ) \subseteq H$, then the Brauer correspondence gives a bijection between the blocks of $R G$ with defect group $D$ and the blocks of $R H$ with defect group $D$. Thus, the number of blocks with non-trivial defect group is $p$-locally determined. |
| | + | |
| | + | There is a close relationship between a block of $R G$ with defect group $D$ and the corresponding block of $RN_G(D)$; however, the investigation of this relationship is far from complete. See, for example, [[McKay–Alperin conjecture|McKay–Alperin conjecture]], the Broué conjecture in [[#References|[a3]]], or the many consequences of the Alperin weight conjecture in [[#References|[a2]]]. |
| | | | |
| | General references in this subject are [[#References|[a1]]], [[#References|[a4]]], [[#References|[a5]]], and [[#References|[a6]]]. | | General references in this subject are [[#References|[a1]]], [[#References|[a4]]], [[#References|[a5]]], and [[#References|[a6]]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.L. Alperin, "Local representation theory" , Cambridge Univ. Press (1986)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.L. Alperin, "Weights for finite groups" P. Fong (ed.) , ''Representations of Finite Groups'' , ''Proc. Symp. Pure Math.'' , '''47''' , Amer. Math. Soc. (1987) pp. 369–379</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Broué, "Isométries parfaites, types de blocs, catégories dérivées" ''Astérisque'' , '''181–182''' (1990) pp. 61–92</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> C. Curtis, I. Reiner, "Methods of representation theory" , '''II''' , Wiley (1987)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W. Feit, "The representation theory of finite groups" , North-Holland (1982)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H. Nagao, Y. Tsushima, "Representation of finite groups" , Acad. Press (1987)</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J.L. Alperin, "Local representation theory" , Cambridge Univ. Press (1986)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> J.L. Alperin, "Weights for finite groups" P. Fong (ed.) , ''Representations of Finite Groups'' , ''Proc. Symp. Pure Math.'' , '''47''' , Amer. Math. Soc. (1987) pp. 369–379</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> M. Broué, "Isométries parfaites, types de blocs, catégories dérivées" ''Astérisque'' , '''181–182''' (1990) pp. 61–92</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> C. Curtis, I. Reiner, "Methods of representation theory" , '''II''' , Wiley (1987)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> W. Feit, "The representation theory of finite groups" , North-Holland (1982)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> H. Nagao, Y. Tsushima, "Representation of finite groups" , Acad. Press (1987)</td></tr></table> |
The $p$-local structure of a finite group $G$, where $p$ is a prime number, is the collection of non-trivial $p$-subgroups of $G$ (cf. also $p$-group), together with their normalizers and centralizers (cf. also Centralizer; Normalizer of a subset). One of the principal goals of representation theory (cf. also Representation of a group) is to find rules relating representations and characters to the various $p$-local structures of $G$. If a prime number $p$ is fixed, representations over fields (cf. also Field) of characteristic $p$, and values of irreducible complex characters on elements of order divisible by $p$, are controlled to a considerable extent by the $p$-local structure. Brauer's three main theorems on blocks are the oldest and most important tools for investigating this phenomenon. (See also Brauer second main theorem; Brauer third main theorem.)
The first step is the partition of indecomposable representations and irreducible characters into blocks. Fix a prime number $p$. Let $R$ be a complete discrete valuation ring of characteristic $0$ with $p$ in its radical $J ( R )$ (cf. also Radical of rings and algebras), let $K$ be its field of fractions, and let $k$ be the residue field $R / J ( R )$. Assume, in addition, that $K$ contains an $e$th root of $1$, where $e$ is the least common multiple of the orders of the elements of $G$. The group algebra $R G$ has a unique decomposition as a direct sum of indecomposable two-sided ideals,
\begin{equation*} R G = B _ { 1 } \bigoplus \ldots \bigoplus B _ { n }. \end{equation*}
The ideals $B _ { i }$ are called the blocks of $R G$. Applying to this decomposition the natural mapping $R G \rightarrow k G$ (i.e. reducing coefficients modulo $J ( R )$), one obtains the unique decomposition of $k G$ as a direct sum of indecomposable two-sided ideals. Any indecomposable $R$-free $R G$-module, or any indecomposable $k G$-module, is annihilated by all blocks except one, and if 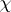 is an irreducible $K$-character of $G$, then $\chi ( B _ { i } ) = 0$ for all but one $i$. Thus, to each block belong a category of $R$-free $R G$-modules, a category of $k G$-modules, and a set of irreducible $K$-characters. The word "block" is sometimes used to refer to the corresponding categories or the corresponding set of characters, rather than to the ideal.
is an irreducible $K$-character of $G$, then $\chi ( B _ { i } ) = 0$ for all but one $i$. Thus, to each block belong a category of $R$-free $R G$-modules, a category of $k G$-modules, and a set of irreducible $K$-characters. The word "block" is sometimes used to refer to the corresponding categories or the corresponding set of characters, rather than to the ideal.
Let $L$ be the subfield of $K$ consisting of all elements that are algebraic over the prime subfield (cf. also Algebraic number). The values on elements of $G$ of any irreducible $K$-character are in $L$. If an imbedding of $L$ in the complex numbers is chosen, the irreducible $K$-characters of $G$ can be identified with the irreducible complex characters of $G$. Thus, the irreducible complex characters are partitioned into blocks. This partition is independent of the choice of the imbedding. When it is not clear from the context which prime number $p$ is intended, one refers to a partition of the irreducible complex characters into $p$-blocks.
To each block is associated a $G$-conjugacy class of $p$-subgroups of $G$, called its defect groups (cf. also Defect group of a block), which substantially control its representation theory. They are defined as follows. Fix a block $B$. For any subgroup $H$ of $G$, let
\begin{equation*} B ^ { H } = \{ a \in B : h ^ { - 1 } a h =a \ \text {for all } h \in H \}. \end{equation*}
Let $T _ { H } ^ { G } : B ^ { H } \rightarrow B ^ { G }$ be given by $T _ { H } ^ { G } ( a ) = \sum _ { j } g _ { j } ^ { - 1 } a g_j$, where $\{ g_j\}$ is a set of representatives for the right cosets of $H$ in $G$. The set of subgroups $H$ minimal such that $B ^ { G } = T _ { H } ^ { G } ( B ^ { H } )$ is a $G$-conjugacy class of $p$-subgroups; they are called the defect groups of $B$. If a block has defect group $1$, then it is isomorphic as an $R$-algebra to a full matrix algebra with entries in $R$, and it is associated to just a single irreducible character, a single indecomposable $R$-free $R G$-module, and a single indecomposable $k G$-module. Blocks with cyclic defect group are very well understood, due to work of E.C. Dade (see [a5], Chap. VII). The process of understanding blocks with more complicated defect groups is still far from complete (as of 1998). For example, R. Brauer has conjectured that the number of irreducible characters belonging to a block with defect group $D$ is less than or equal to the order of $D$. See also Brauer height-zero conjecture.
The Brauer correspondence is a tool for relating blocks of $G$ to blocks of subgroups of $G$; it is defined as follows. The algebra $R G$ is a right module over 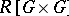 , with $a ( g h ) = g ^ { - 1 } a h$ for all $g \in G$, $h \in G$, and $a \in R G$. The decomposition of $R G$ into blocks is also a decomposition of $R G$ as a direct sum of indecomposable
, with $a ( g h ) = g ^ { - 1 } a h$ for all $g \in G$, $h \in G$, and $a \in R G$. The decomposition of $R G$ into blocks is also a decomposition of $R G$ as a direct sum of indecomposable 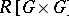 -modules. Let $H$ be a subgroup of $G$ and let $b$ be a block of $R H$. If there is a unique block $B$ of $G$ with $b$ isomorphic as an $R [ H \times H]$-module to a direct summand of the restriction $B _ { R [ H \times H ]}$, then one says that $b ^ { G }$ is defined and $B = b ^ { G }$. The mapping $b \mapsto b ^ { G }$ is called the Brauer correspondence. Let $D$ be a defect group of $b$. Assume that $C _ { G } ( D ) \subseteq H$; then in any decomposition of $R G$ as a direct sum of indecomposable $R [ H \times H]$-modules there is a unique module isomorphic to $b$; so certainly $b ^ { G }$ is defined. Most of the important applications of the Brauer correspondence arise in this way.
-modules. Let $H$ be a subgroup of $G$ and let $b$ be a block of $R H$. If there is a unique block $B$ of $G$ with $b$ isomorphic as an $R [ H \times H]$-module to a direct summand of the restriction $B _ { R [ H \times H ]}$, then one says that $b ^ { G }$ is defined and $B = b ^ { G }$. The mapping $b \mapsto b ^ { G }$ is called the Brauer correspondence. Let $D$ be a defect group of $b$. Assume that $C _ { G } ( D ) \subseteq H$; then in any decomposition of $R G$ as a direct sum of indecomposable $R [ H \times H]$-modules there is a unique module isomorphic to $b$; so certainly $b ^ { G }$ is defined. Most of the important applications of the Brauer correspondence arise in this way.
Brauer's original definition of this correspondence in terms of central characters (see [a5], Chap. III) yields a mapping that has a slightly different domain of definition from the mapping described here. The mappings agree on the intersection of their domains, and both are defined in the important case when $C _ { G } ( D ) \subseteq H$.
Brauer's first main theorem says that if $D$ is a $p$-subgroup of $G$ and $H$ is a subgroup of $G$ with $N _ { G } ( D ) \subseteq H$, then the Brauer correspondence gives a bijection between the blocks of $R G$ with defect group $D$ and the blocks of $R H$ with defect group $D$. Thus, the number of blocks with non-trivial defect group is $p$-locally determined.
There is a close relationship between a block of $R G$ with defect group $D$ and the corresponding block of $RN_G(D)$; however, the investigation of this relationship is far from complete. See, for example, McKay–Alperin conjecture, the Broué conjecture in [a3], or the many consequences of the Alperin weight conjecture in [a2].
General references in this subject are [a1], [a4], [a5], and [a6].
References
| [a1] | J.L. Alperin, "Local representation theory" , Cambridge Univ. Press (1986) |
| [a2] | J.L. Alperin, "Weights for finite groups" P. Fong (ed.) , Representations of Finite Groups , Proc. Symp. Pure Math. , 47 , Amer. Math. Soc. (1987) pp. 369–379 |
| [a3] | M. Broué, "Isométries parfaites, types de blocs, catégories dérivées" Astérisque , 181–182 (1990) pp. 61–92 |
| [a4] | C. Curtis, I. Reiner, "Methods of representation theory" , II , Wiley (1987) |
| [a5] | W. Feit, "The representation theory of finite groups" , North-Holland (1982) |
| [a6] | H. Nagao, Y. Tsushima, "Representation of finite groups" , Acad. Press (1987) |
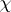 is an irreducible $K$-character of $G$, then $\chi ( B _ { i } ) = 0$ for all but one $i$. Thus, to each block belong a category of $R$-free $R G$-modules, a category of $k G$-modules, and a set of irreducible $K$-characters. The word "block" is sometimes used to refer to the corresponding categories or the corresponding set of characters, rather than to the ideal.
is an irreducible $K$-character of $G$, then $\chi ( B _ { i } ) = 0$ for all but one $i$. Thus, to each block belong a category of $R$-free $R G$-modules, a category of $k G$-modules, and a set of irreducible $K$-characters. The word "block" is sometimes used to refer to the corresponding categories or the corresponding set of characters, rather than to the ideal.
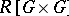 , with $a ( g h ) = g ^ { - 1 } a h$ for all $g \in G$, $h \in G$, and $a \in R G$. The decomposition of $R G$ into blocks is also a decomposition of $R G$ as a direct sum of indecomposable
, with $a ( g h ) = g ^ { - 1 } a h$ for all $g \in G$, $h \in G$, and $a \in R G$. The decomposition of $R G$ into blocks is also a decomposition of $R G$ as a direct sum of indecomposable 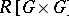 -modules. Let $H$ be a subgroup of $G$ and let $b$ be a block of $R H$. If there is a unique block $B$ of $G$ with $b$ isomorphic as an $R [ H \times H]$-module to a direct summand of the restriction $B _ { R [ H \times H ]}$, then one says that $b ^ { G }$ is defined and $B = b ^ { G }$. The mapping $b \mapsto b ^ { G }$ is called the Brauer correspondence. Let $D$ be a defect group of $b$. Assume that $C _ { G } ( D ) \subseteq H$; then in any decomposition of $R G$ as a direct sum of indecomposable $R [ H \times H]$-modules there is a unique module isomorphic to $b$; so certainly $b ^ { G }$ is defined. Most of the important applications of the Brauer correspondence arise in this way.
-modules. Let $H$ be a subgroup of $G$ and let $b$ be a block of $R H$. If there is a unique block $B$ of $G$ with $b$ isomorphic as an $R [ H \times H]$-module to a direct summand of the restriction $B _ { R [ H \times H ]}$, then one says that $b ^ { G }$ is defined and $B = b ^ { G }$. The mapping $b \mapsto b ^ { G }$ is called the Brauer correspondence. Let $D$ be a defect group of $b$. Assume that $C _ { G } ( D ) \subseteq H$; then in any decomposition of $R G$ as a direct sum of indecomposable $R [ H \times H]$-modules there is a unique module isomorphic to $b$; so certainly $b ^ { G }$ is defined. Most of the important applications of the Brauer correspondence arise in this way.