Difference between revisions of "Abstract parabolic differential equation"
(Importing text file) |
(details) |
||
| (3 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 127 formulas, 125 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
An equation of the form | An equation of the form | ||
| − | + | \begin{equation} \tag{a1} \frac { d u ( t ) } { d t } = A ( t ) u ( t ) + f ( t ) , \quad 0 < t \leq T, \end{equation} | |
| − | where for each | + | where for each $t \in [ 0 , T]$, $A ( t )$ is the infinitesimal generator of an analytic semi-group (cf. also [[Semi-group of operators|Semi-group of operators]]; [[Strongly-continuous semi-group|Strongly-continuous semi-group]]) in some [[Banach space|Banach space]] $X$. Hence, without loss of generality it is always assumed that |
| − | I) there exist an angle | + | I) there exist an angle $\theta _ { 0 } \in ( \pi / 2 , \pi )$ and a positive constant $M$ such that |
| − | i) | + | i) $\rho ( A ( t ) ) \supset S _ { \theta _ { 0 } } = \{ z \in {\bf C} : | \operatorname { arg } z | \leq \theta _ { 0 } \} \cup \{ 0 \}$, $t \in [ 0 , T]$; |
| − | ii) | + | ii) $\| ( \lambda - A ( t ) ) ^ { - 1 } \| \leq M / ( 1 + | \lambda | )$, $\lambda \in S _ { \theta _ { 0 } }$, $t \in [ 0 , T]$. The domain $D ( A ( t ) )$ of $A ( t )$ is not necessarily dense. Various results on the solvability of the initial value problem for (a1) have been published. The main object is to construct the fundamental solution $U ( t , s ) , 0 \leq s \leq t \leq T$ (cf. also [[Fundamental solution|Fundamental solution]]), which is an operator-valued function satisfying |
| − | + | \begin{equation*} \frac { \partial } { \partial t } U ( t , s ) - A ( t ) U ( t , s ) = 0 \end{equation*} | |
| − | + | \begin{equation*} \frac { \partial } { \partial s } U ( t , s ) + U ( t , s ) A ( s ) = 0 , \operatorname { lim } _ { t \rightarrow s } U ( t , s ) x = x \text { for } x \in \overline { D ( A ( s ) ) }. \end{equation*} | |
The solution of (a1) satisfying the initial condition | The solution of (a1) satisfying the initial condition | ||
| − | + | \begin{equation} \tag{a2} u ( 0 ) = u _ { 0 } \in \overline { D ( A ( 0 ) ) }, \end{equation} | |
if it exists, is given by | if it exists, is given by | ||
| − | + | \begin{equation} \tag{a3} u ( t ) = U ( t , 0 ) u _ { 0 } + \int _ { 0 } ^ { t } U ( t , s ) f ( s ) d s. \end{equation} | |
In parabolic cases, the fundamental solution usually satisfies the inequality | In parabolic cases, the fundamental solution usually satisfies the inequality | ||
| − | + | \begin{equation*} \| \frac { \partial U ( t , s ) } { \partial t } \| \leq \frac { C } { t - s } , \quad s , t \in [ 0 , T ], \end{equation*} | |
| − | for some constant | + | for some constant $C > 0$. |
One of the most general result is due to P. Acquistapace and B. Terreni [[#References|[a3]]], [[#References|[a4]]]. Suppose that | One of the most general result is due to P. Acquistapace and B. Terreni [[#References|[a3]]], [[#References|[a4]]]. Suppose that | ||
| − | II) there exist a constant | + | II) there exist a constant $K _ { 0 } > 0$ and a set of real numbers $\alpha _ { 1 } , \ldots , \alpha _ { k } , \beta _ { 1 } , \ldots , \beta _ { k }$ with $0 \leq \beta _ { i } < \alpha _ { i } \leq 2$, $i = 1 , \ldots , k$, such that |
| − | + | \begin{equation*} | A ( t ) ( \lambda - A ( t ) ) ^ { - 1 } ( A ( t ) ^ { - 1 } - A ( s ) ^ { - 1 } ) \| \leq \end{equation*} | |
| − | + | \begin{equation*} \leq K _ { 0 } \sum _ { i = 1 } ^ { k } ( t - s ) ^ { \alpha _ { i } } | \lambda | ^ { \beta _ { i } - 1 } , \lambda \in S _ { \theta _ { 0 } } \backslash \{ 0 \} , \quad 0 \leq s \leq t \leq T. \end{equation*} | |
| − | Then the fundamental solution exists, and if | + | Then the fundamental solution exists, and if $u_{0}$ satisfies (a2) and $f ( . )$ is Hölder continuous (i.e., $f \in C ^ { \alpha } ( [ 0 , T ] ; X )$ for some $\alpha \in ( 0,1 ]$, i.e. |
| − | + | \begin{equation} \tag{a4} \| f ( t ) - f ( s ) \| \leq C _ { 1 } | t - s | ^ { \alpha } , \quad 0 \leq s \leq t \leq T; \end{equation} | |
| − | cf. also [[Hölder condition|Hölder condition]]), then the function (a3) is the unique solution of (a1), (a2) in the following sense: | + | cf. also [[Hölder condition|Hölder condition]]), then the function (a3) is the unique solution of (a1), (a2) in the following sense: $u \in C ( [ 0 , T ] ; X ) \cap C ^ { 1 } ( ( 0 , T ] ; X )$, $u ( t ) \in D ( A ( t ) )$ for $t \in ( 0 , T ]$, $A u \in C ( ( 0 , T ] ; X )$, (a1) holds for $t \in ( 0 , T ]$ and (a2) holds. A solution in this sense is usually called a classical solution. If, moreover, $u _ { 0 } \in D ( A ( 0 ) )$ and $A ( 0 ) u_0 + f ( 0 ) \in \overline { D ( A ( 0 ) ) }$, then $u \in C ^ { 1 } ( [ 0 , T ] ; X )$, $u ( t ) \in D ( A ( t ) )$ for $t \in [ 0 , T]$, $A u \in C ( [ 0 , T ] ; X )$ and (a1) is satisfied in $[0 , T]$. Such a solution is usually called a strict solution. |
The following results on maximal regularity are well known. | The following results on maximal regularity are well known. | ||
===Time regularity.=== | ===Time regularity.=== | ||
| − | Let | + | Let $u _ { 0 } \in D ( A ( 0 ) )$ and $f \in C ^ { \alpha } ( [ 0 , T ] ; X )$. Then |
| − | + | \begin{equation*} u ^ { \prime } \in C ^ { \alpha } ( [ 0 , T ] ; X ) \bigcap B ( D _ { A } ( \alpha , \infty ) ), \end{equation*} | |
| − | + | \begin{equation*} A u \in C ^ { \alpha } ( [ 0 , T ] ; X ) \end{equation*} | |
| − | if and only if | + | if and only if $A ( 0 ) u _ { 0 } + f ( 0 ) \in D _ { A ( 0 ) } ( \alpha , \infty )$, where $B ( D _ { A } ( \alpha , \infty ) )$ is the set of all functions $f \in L ^ { \infty } ( 0 , T ; X )$ such that $f ( t ) \in D _ { A ( t ) } ( \alpha , \infty )$ (an interpolation space between $D ( A ( t ) )$ and $X$; cf. also [[Interpolation of operators|Interpolation of operators]]) for almost all $t \in [ 0 , T]$ and the norm of $f ( t )$ on $D _ { A ( t ) } ( \alpha , \infty )$ is essentially bounded in $[0 , T]$. |
===Space regularity.=== | ===Space regularity.=== | ||
| − | Let | + | Let $u _ { 0 } \in D ( A ( 0 ) )$ and $f \in B ( D _ { A } ( \alpha , \infty ) )$. Then |
| − | + | \begin{equation*} u ^ { \prime } \in B ( D _ { A } ( \alpha , \infty ) ), \end{equation*} | |
| − | + | \begin{equation*} A u \in B ( D _ { A } ( \alpha , \infty ) ) \bigcap C ^ { \alpha } ( [ 0 , T ] ; X ) \end{equation*} | |
| − | if and only if | + | if and only if $A ( 0 ) u _ { 0 } \in D _ { A ( 0 ) } ( \alpha , \infty )$. |
| − | Hypothesis II) holds if the domain | + | Hypothesis II) holds if the domain $D ( A ( t ) )$ is independent of $t$ and $t \mapsto A ( t )$ is Hölder continuous, i.e. there exist constants $C _ { 2 } > 0$ and $\alpha \in ( 0,1 ]$ such that |
| − | + | \begin{equation*} | ( A ( t ) - A ( s ) ) A ( 0 ) ^ { - 1 } \| \leq C _ { 2 } | t - s | ^ { \alpha } , \quad t , s \in [ 0 , T ]. \end{equation*} | |
Another main result by Acquistapace and Terreni is the following ([[#References|[a2]]]): | Another main result by Acquistapace and Terreni is the following ([[#References|[a2]]]): | ||
| − | III.i) | + | III.i) $t \mapsto A ( t ) ^ { - 1 }$ is differentiable and there exist constants $K _ { 1 } > 0$ and $\rho \in ( 0,1 ]$ such that |
| − | + | \begin{equation*} \left\| \frac { \partial } { \partial t } ( \lambda - A ( t ) ) ^ { - 1 } \right\| \leq \frac { K _ { 1 } } { ( 1 + | \lambda | ) ^ { \rho } }, \end{equation*} | |
| − | + | \begin{equation*} \lambda \in S _ { \theta _ { 0 } } , t \in [ 0 , T ]; \end{equation*} | |
| − | III.ii) there exist constants | + | III.ii) there exist constants $K _ { 2 } > 0$ and $\eta \in ( 0,1 ]$ such that |
| − | + | \begin{equation*} \| \frac { d } { d t } A ( t ) ^ { - 1 } - \frac { d } { d s } A ( s ) ^ { - 1 } \| \leq K _ { 2 } | t - s | ^ { \eta }, \end{equation*} | |
| − | + | \begin{equation*} t , s \in [ 0 , T ]. \end{equation*} | |
| − | If | + | If $A ( t )$ is densely defined, this case reduces to the one in [[#References|[a8]]]. Under the assumptions I), III) it can be shown that for $u_{0}$ and $f$ satisfying (a2) and (a4), a classical solution of (a1) exists and is unique. The solution is strict if, moreover, $u _ { 0 } \in D ( A ( 0 ) )$ and |
| − | + | \begin{equation} \tag{a5} A ( 0 ) u _ { 0 } + f ( 0 ) - \frac { d } { d t } A ( t ) ^ { - 1 } | _ { t = 0 } A ( 0 ) u _ { 0 } \in \overline { D ( A ( 0 ) ) }. \end{equation} | |
| − | The following maximal regularity result holds: If | + | The following maximal regularity result holds: If $u _ { 0 } \in D ( A ( 0 ) )$ and $f \in C ^ { \delta } ( [ 0 , T ] ; X )$ for $\delta \in ( 0 , \eta ) \cap ( 0 , \rho ]$, then the solution of (a1) belongs to $C ^ { 1 + \delta } ( [ 0 , T ] ; X )$ if and only if the left-hand side of (a5) belongs to $D _ { A ( 0 ) } ( \delta , \infty )$. |
Another of general results is due to A. Yagi [[#References|[a10]]], where the fundamental solution is constructed under the following assumptions: | Another of general results is due to A. Yagi [[#References|[a10]]], where the fundamental solution is constructed under the following assumptions: | ||
| − | IV) hypothesis III.i) is satisfied, and there exist constants | + | IV) hypothesis III.i) is satisfied, and there exist constants $K _ { 3 }$ and a non-empty set of indices $\{ ( \alpha _ { i } , \beta _ { i } ) : i = 1 , \ldots , k \}$ satisfying $- 1 \leq \alpha _ { i } < \beta _ { i } \leq 1$ such that |
| − | + | \begin{equation*} \left| A ( t ) ( \lambda - A ( t ) ) ^ { - 1 } \frac { d A ( t ) ^ { - 1 } } { d t } + \right. \end{equation*} | |
| − | + | \begin{equation*} \left. - A ( s ) ( \lambda - A ( s ) ) ^ { - 1 } \frac { d A ( s ) ^ { - 1 } } { d s } \right\| \leq \end{equation*} | |
| − | + | \begin{equation*} \leq K _ { 2 } \sum _ { i = 1 } ^ { k } | \lambda | ^ { \alpha _ { i } } | t - s | ^ { \beta _ { i } }, \end{equation*} | |
| − | + | \begin{equation*} \lambda \in S _ { \theta _ { 0 } } , \quad t , s \in [ 0 , T ]. \end{equation*} | |
It is shown in [[#References|[a4]]] that the above three results are independent of one another. | It is shown in [[#References|[a4]]] that the above three results are independent of one another. | ||
| Line 103: | Line 111: | ||
The above results are applied to initial-boundary value problems for parabolic partial differential equations: | The above results are applied to initial-boundary value problems for parabolic partial differential equations: | ||
| − | + | \begin{equation*} \frac { \partial u } { \partial t } = L ( t , x , D _ { x } ) u + f ( t , x ) \text { in } [ 0 , T ] \times \Omega, \end{equation*} | |
| − | + | \begin{equation*} B _ { j } ( t , x , D _ { x } ) u = 0 , \text { on } [ 0 , T ] \times \partial \Omega ,\quad j = 1 , \ldots , m, \end{equation*} | |
| − | where | + | where $L ( t , x , D _ { x } )$ is an elliptic operator of order $2 m$ (cf. also [[Elliptic partial differential equation|Elliptic partial differential equation]]), $\{ B _ { j } ( t , x , D _ { x } ) \} _ { j = 1 } ^ { m }$ are operators of order $< 2 m$ for each $t \in [ 0 , T]$, and $\Omega$ is a usually bounded open set in ${\bf R} ^ { n }$, $n \geq 1$, with smooth boundary $\partial \Omega$. Under some algebraic assumptions on the operators $L ( t , x , D _ { x } )$, $\{ B _ { j } ( t , x , D _ { x } ) \} _ { j = 1 } ^ { m }$ and smoothness hypotheses of the coefficients, it is shown in [[#References|[a1]]] that the operator-valued function $A ( t )$ defined by |
| − | + | \begin{equation*} D ( A ( t ) ) = \end{equation*} | |
| − | + | \begin{equation*} \left\{ u \in \cap _ { q \in ( n , \infty ) } W ^ { 2 m , q } ( \Omega ) : \begin{array}{l} { L(t, \cdot , D_x) u \in C ( \overline { \Omega } ), } \\ {B _ { j } ( t , \cdot , D _ { x } ) u=0 \ \text{ on } \partial \Omega,} \\ {j=1, \dots , m} \end{array} \right\},\; A(t)u=L(\cdot , t , D_x)u \ \text{ for } \ u \in D(A(t)), \end{equation*} | |
| − | satisfies the assumptions I) and II) in the space | + | satisfies the assumptions I) and II) in the space $C ( \overline { \Omega } )$ if some negative constant is added to $L ( x , t , D _ { x } )$ if necessary (this is not an essential restriction). The regularity of the coefficients here is Hölder continuity with some exponent. An analogous result holds for the operator defined in $L ^ { p } ( \Omega )$, $1 < p < \infty$ by |
| − | + | \begin{equation*} D ( A ( t ) ) = \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120070/a120070116.png"/></td> </tr></table> |
| − | + | \begin{equation*} A ( t ) u = L ( . , t , D _ { x } ) u\text { for } u \in D ( A ( t ) ). \end{equation*} | |
There is also extensive literature on non-linear equations; see [[#References|[a7]]] and [[#References|[a9]]] for details. The following result on the quasi-linear partial differential equation | There is also extensive literature on non-linear equations; see [[#References|[a7]]] and [[#References|[a9]]] for details. The following result on the quasi-linear partial differential equation | ||
| − | + | \begin{equation} \tag{a6} \frac { d u } { d t } = A ( t , u ) u + f ( t , u ) \end{equation} | |
| − | is due to H. Amann [[#References|[a5]]], [[#References|[a6]]]: For a given function | + | is due to H. Amann [[#References|[a5]]], [[#References|[a6]]]: For a given function $v$, let $u ( v )$ be the solution of the linear problem |
| − | + | \begin{equation} \tag{a7} \frac { d u } { d t } = A ( t , v ) u + f ( t , v ) , 0 < t \leq T , u ( 0 ) = u_0. \end{equation} | |
| − | If the problem is extended to a larger space so that the domains of the extensions of | + | If the problem is extended to a larger space so that the domains of the extensions of $A ( t , v )$ are independent of $( t , v )$, then, under a weak regularity hypothesis for $A ( t , v )$ on $( t , v )$, the fundamental solution for the equation (a7) can be constructed, and a fixed-point theorem can be applied to the mapping $v \mapsto u ( v )$ to solve the equation (a6). The result has been applied to quasi-linear parabolic partial differential equations with quasi-linear boundary conditions. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> P. Acquistapace, "Evolution operators and strong solutions of abstract linear parabolic equations" ''Diff. and Integral Eq.'' , '''1''' (1988) pp. 433–457</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> P. Acquistapace, B. Terreni, "Some existence and regularity results for abstract non-autonomous parabolic equations" ''J. Math. Anal. Appl.'' , '''99''' (1984) pp. 9–64</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> P. Acquistapace, B. Terreni, "On fundamental solutions for abstract parabolic equations" A. Favini (ed.) E. Obrecht (ed.) , ''Differential Equations in Banach Spaces, Bologna, 1985'' , ''Lecture Notes Math.'' , '''1223''' , Springer (1986) pp. 1–11</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> P. Acquistapace, B. Terreni, "A unified approach to abstract linear non-autonomous parabolic equations" ''Rend. Sem. Univ. Padova'' , '''78''' (1987) pp. 47–107</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> H. Amann, "Quasilinear parabolic systems under nonlinear boundary conditions" ''Arch. Rat. Mech. Anal.'' , '''92''' (1986) pp. 153–192</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> H. Amann, "On abstract parabolic fundamental solutions" ''J. Math. Soc. Japan'' , '''39''' (1987) pp. 93–116</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> H. Amann, "Linear and quasilinear parabolic problems I: Abstract linear theory" , ''Monogr. Math.'' , '''89''' , Birkhäuser (1995)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> T. Kato, H. Tanabe, "On the abstract evolution equation" ''Osaka Math. J.'' , '''14''' (1962) pp. 107–133</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> A. Lunardi, "Analytic semigroups and optimal regularity in parabolic problems" , ''Progr. Nonlinear Diff. Eqns. Appl.'' , '''16''' , Birkhäuser (1995)</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> A. Yagi, "On the abstract evolution equation of parablic type" ''Osaka J. Math.'' , '''14''' (1977) pp. 557–568</td></tr></table> |
Latest revision as of 18:47, 26 January 2024
An equation of the form
\begin{equation} \tag{a1} \frac { d u ( t ) } { d t } = A ( t ) u ( t ) + f ( t ) , \quad 0 < t \leq T, \end{equation}
where for each $t \in [ 0 , T]$, $A ( t )$ is the infinitesimal generator of an analytic semi-group (cf. also Semi-group of operators; Strongly-continuous semi-group) in some Banach space $X$. Hence, without loss of generality it is always assumed that
I) there exist an angle $\theta _ { 0 } \in ( \pi / 2 , \pi )$ and a positive constant $M$ such that
i) $\rho ( A ( t ) ) \supset S _ { \theta _ { 0 } } = \{ z \in {\bf C} : | \operatorname { arg } z | \leq \theta _ { 0 } \} \cup \{ 0 \}$, $t \in [ 0 , T]$;
ii) $\| ( \lambda - A ( t ) ) ^ { - 1 } \| \leq M / ( 1 + | \lambda | )$, $\lambda \in S _ { \theta _ { 0 } }$, $t \in [ 0 , T]$. The domain $D ( A ( t ) )$ of $A ( t )$ is not necessarily dense. Various results on the solvability of the initial value problem for (a1) have been published. The main object is to construct the fundamental solution $U ( t , s ) , 0 \leq s \leq t \leq T$ (cf. also Fundamental solution), which is an operator-valued function satisfying
\begin{equation*} \frac { \partial } { \partial t } U ( t , s ) - A ( t ) U ( t , s ) = 0 \end{equation*}
\begin{equation*} \frac { \partial } { \partial s } U ( t , s ) + U ( t , s ) A ( s ) = 0 , \operatorname { lim } _ { t \rightarrow s } U ( t , s ) x = x \text { for } x \in \overline { D ( A ( s ) ) }. \end{equation*}
The solution of (a1) satisfying the initial condition
\begin{equation} \tag{a2} u ( 0 ) = u _ { 0 } \in \overline { D ( A ( 0 ) ) }, \end{equation}
if it exists, is given by
\begin{equation} \tag{a3} u ( t ) = U ( t , 0 ) u _ { 0 } + \int _ { 0 } ^ { t } U ( t , s ) f ( s ) d s. \end{equation}
In parabolic cases, the fundamental solution usually satisfies the inequality
\begin{equation*} \| \frac { \partial U ( t , s ) } { \partial t } \| \leq \frac { C } { t - s } , \quad s , t \in [ 0 , T ], \end{equation*}
for some constant $C > 0$.
One of the most general result is due to P. Acquistapace and B. Terreni [a3], [a4]. Suppose that
II) there exist a constant $K _ { 0 } > 0$ and a set of real numbers $\alpha _ { 1 } , \ldots , \alpha _ { k } , \beta _ { 1 } , \ldots , \beta _ { k }$ with $0 \leq \beta _ { i } < \alpha _ { i } \leq 2$, $i = 1 , \ldots , k$, such that
\begin{equation*} | A ( t ) ( \lambda - A ( t ) ) ^ { - 1 } ( A ( t ) ^ { - 1 } - A ( s ) ^ { - 1 } ) \| \leq \end{equation*}
\begin{equation*} \leq K _ { 0 } \sum _ { i = 1 } ^ { k } ( t - s ) ^ { \alpha _ { i } } | \lambda | ^ { \beta _ { i } - 1 } , \lambda \in S _ { \theta _ { 0 } } \backslash \{ 0 \} , \quad 0 \leq s \leq t \leq T. \end{equation*}
Then the fundamental solution exists, and if $u_{0}$ satisfies (a2) and $f ( . )$ is Hölder continuous (i.e., $f \in C ^ { \alpha } ( [ 0 , T ] ; X )$ for some $\alpha \in ( 0,1 ]$, i.e.
\begin{equation} \tag{a4} \| f ( t ) - f ( s ) \| \leq C _ { 1 } | t - s | ^ { \alpha } , \quad 0 \leq s \leq t \leq T; \end{equation}
cf. also Hölder condition), then the function (a3) is the unique solution of (a1), (a2) in the following sense: $u \in C ( [ 0 , T ] ; X ) \cap C ^ { 1 } ( ( 0 , T ] ; X )$, $u ( t ) \in D ( A ( t ) )$ for $t \in ( 0 , T ]$, $A u \in C ( ( 0 , T ] ; X )$, (a1) holds for $t \in ( 0 , T ]$ and (a2) holds. A solution in this sense is usually called a classical solution. If, moreover, $u _ { 0 } \in D ( A ( 0 ) )$ and $A ( 0 ) u_0 + f ( 0 ) \in \overline { D ( A ( 0 ) ) }$, then $u \in C ^ { 1 } ( [ 0 , T ] ; X )$, $u ( t ) \in D ( A ( t ) )$ for $t \in [ 0 , T]$, $A u \in C ( [ 0 , T ] ; X )$ and (a1) is satisfied in $[0 , T]$. Such a solution is usually called a strict solution.
The following results on maximal regularity are well known.
Time regularity.
Let $u _ { 0 } \in D ( A ( 0 ) )$ and $f \in C ^ { \alpha } ( [ 0 , T ] ; X )$. Then
\begin{equation*} u ^ { \prime } \in C ^ { \alpha } ( [ 0 , T ] ; X ) \bigcap B ( D _ { A } ( \alpha , \infty ) ), \end{equation*}
\begin{equation*} A u \in C ^ { \alpha } ( [ 0 , T ] ; X ) \end{equation*}
if and only if $A ( 0 ) u _ { 0 } + f ( 0 ) \in D _ { A ( 0 ) } ( \alpha , \infty )$, where $B ( D _ { A } ( \alpha , \infty ) )$ is the set of all functions $f \in L ^ { \infty } ( 0 , T ; X )$ such that $f ( t ) \in D _ { A ( t ) } ( \alpha , \infty )$ (an interpolation space between $D ( A ( t ) )$ and $X$; cf. also Interpolation of operators) for almost all $t \in [ 0 , T]$ and the norm of $f ( t )$ on $D _ { A ( t ) } ( \alpha , \infty )$ is essentially bounded in $[0 , T]$.
Space regularity.
Let $u _ { 0 } \in D ( A ( 0 ) )$ and $f \in B ( D _ { A } ( \alpha , \infty ) )$. Then
\begin{equation*} u ^ { \prime } \in B ( D _ { A } ( \alpha , \infty ) ), \end{equation*}
\begin{equation*} A u \in B ( D _ { A } ( \alpha , \infty ) ) \bigcap C ^ { \alpha } ( [ 0 , T ] ; X ) \end{equation*}
if and only if $A ( 0 ) u _ { 0 } \in D _ { A ( 0 ) } ( \alpha , \infty )$.
Hypothesis II) holds if the domain $D ( A ( t ) )$ is independent of $t$ and $t \mapsto A ( t )$ is Hölder continuous, i.e. there exist constants $C _ { 2 } > 0$ and $\alpha \in ( 0,1 ]$ such that
\begin{equation*} | ( A ( t ) - A ( s ) ) A ( 0 ) ^ { - 1 } \| \leq C _ { 2 } | t - s | ^ { \alpha } , \quad t , s \in [ 0 , T ]. \end{equation*}
Another main result by Acquistapace and Terreni is the following ([a2]):
III.i) $t \mapsto A ( t ) ^ { - 1 }$ is differentiable and there exist constants $K _ { 1 } > 0$ and $\rho \in ( 0,1 ]$ such that
\begin{equation*} \left\| \frac { \partial } { \partial t } ( \lambda - A ( t ) ) ^ { - 1 } \right\| \leq \frac { K _ { 1 } } { ( 1 + | \lambda | ) ^ { \rho } }, \end{equation*}
\begin{equation*} \lambda \in S _ { \theta _ { 0 } } , t \in [ 0 , T ]; \end{equation*}
III.ii) there exist constants $K _ { 2 } > 0$ and $\eta \in ( 0,1 ]$ such that
\begin{equation*} \| \frac { d } { d t } A ( t ) ^ { - 1 } - \frac { d } { d s } A ( s ) ^ { - 1 } \| \leq K _ { 2 } | t - s | ^ { \eta }, \end{equation*}
\begin{equation*} t , s \in [ 0 , T ]. \end{equation*}
If $A ( t )$ is densely defined, this case reduces to the one in [a8]. Under the assumptions I), III) it can be shown that for $u_{0}$ and $f$ satisfying (a2) and (a4), a classical solution of (a1) exists and is unique. The solution is strict if, moreover, $u _ { 0 } \in D ( A ( 0 ) )$ and
\begin{equation} \tag{a5} A ( 0 ) u _ { 0 } + f ( 0 ) - \frac { d } { d t } A ( t ) ^ { - 1 } | _ { t = 0 } A ( 0 ) u _ { 0 } \in \overline { D ( A ( 0 ) ) }. \end{equation}
The following maximal regularity result holds: If $u _ { 0 } \in D ( A ( 0 ) )$ and $f \in C ^ { \delta } ( [ 0 , T ] ; X )$ for $\delta \in ( 0 , \eta ) \cap ( 0 , \rho ]$, then the solution of (a1) belongs to $C ^ { 1 + \delta } ( [ 0 , T ] ; X )$ if and only if the left-hand side of (a5) belongs to $D _ { A ( 0 ) } ( \delta , \infty )$.
Another of general results is due to A. Yagi [a10], where the fundamental solution is constructed under the following assumptions:
IV) hypothesis III.i) is satisfied, and there exist constants $K _ { 3 }$ and a non-empty set of indices $\{ ( \alpha _ { i } , \beta _ { i } ) : i = 1 , \ldots , k \}$ satisfying $- 1 \leq \alpha _ { i } < \beta _ { i } \leq 1$ such that
\begin{equation*} \left| A ( t ) ( \lambda - A ( t ) ) ^ { - 1 } \frac { d A ( t ) ^ { - 1 } } { d t } + \right. \end{equation*}
\begin{equation*} \left. - A ( s ) ( \lambda - A ( s ) ) ^ { - 1 } \frac { d A ( s ) ^ { - 1 } } { d s } \right\| \leq \end{equation*}
\begin{equation*} \leq K _ { 2 } \sum _ { i = 1 } ^ { k } | \lambda | ^ { \alpha _ { i } } | t - s | ^ { \beta _ { i } }, \end{equation*}
\begin{equation*} \lambda \in S _ { \theta _ { 0 } } , \quad t , s \in [ 0 , T ]. \end{equation*}
It is shown in [a4] that the above three results are independent of one another.
The above results are applied to initial-boundary value problems for parabolic partial differential equations:
\begin{equation*} \frac { \partial u } { \partial t } = L ( t , x , D _ { x } ) u + f ( t , x ) \text { in } [ 0 , T ] \times \Omega, \end{equation*}
\begin{equation*} B _ { j } ( t , x , D _ { x } ) u = 0 , \text { on } [ 0 , T ] \times \partial \Omega ,\quad j = 1 , \ldots , m, \end{equation*}
where $L ( t , x , D _ { x } )$ is an elliptic operator of order $2 m$ (cf. also Elliptic partial differential equation), $\{ B _ { j } ( t , x , D _ { x } ) \} _ { j = 1 } ^ { m }$ are operators of order $< 2 m$ for each $t \in [ 0 , T]$, and $\Omega$ is a usually bounded open set in ${\bf R} ^ { n }$, $n \geq 1$, with smooth boundary $\partial \Omega$. Under some algebraic assumptions on the operators $L ( t , x , D _ { x } )$, $\{ B _ { j } ( t , x , D _ { x } ) \} _ { j = 1 } ^ { m }$ and smoothness hypotheses of the coefficients, it is shown in [a1] that the operator-valued function $A ( t )$ defined by
\begin{equation*} D ( A ( t ) ) = \end{equation*}
\begin{equation*} \left\{ u \in \cap _ { q \in ( n , \infty ) } W ^ { 2 m , q } ( \Omega ) : \begin{array}{l} { L(t, \cdot , D_x) u \in C ( \overline { \Omega } ), } \\ {B _ { j } ( t , \cdot , D _ { x } ) u=0 \ \text{ on } \partial \Omega,} \\ {j=1, \dots , m} \end{array} \right\},\; A(t)u=L(\cdot , t , D_x)u \ \text{ for } \ u \in D(A(t)), \end{equation*}
satisfies the assumptions I) and II) in the space $C ( \overline { \Omega } )$ if some negative constant is added to $L ( x , t , D _ { x } )$ if necessary (this is not an essential restriction). The regularity of the coefficients here is Hölder continuity with some exponent. An analogous result holds for the operator defined in $L ^ { p } ( \Omega )$, $1 < p < \infty$ by
\begin{equation*} D ( A ( t ) ) = \end{equation*}
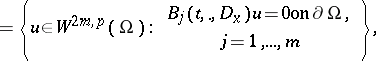 |
\begin{equation*} A ( t ) u = L ( . , t , D _ { x } ) u\text { for } u \in D ( A ( t ) ). \end{equation*}
There is also extensive literature on non-linear equations; see [a7] and [a9] for details. The following result on the quasi-linear partial differential equation
\begin{equation} \tag{a6} \frac { d u } { d t } = A ( t , u ) u + f ( t , u ) \end{equation}
is due to H. Amann [a5], [a6]: For a given function $v$, let $u ( v )$ be the solution of the linear problem
\begin{equation} \tag{a7} \frac { d u } { d t } = A ( t , v ) u + f ( t , v ) , 0 < t \leq T , u ( 0 ) = u_0. \end{equation}
If the problem is extended to a larger space so that the domains of the extensions of $A ( t , v )$ are independent of $( t , v )$, then, under a weak regularity hypothesis for $A ( t , v )$ on $( t , v )$, the fundamental solution for the equation (a7) can be constructed, and a fixed-point theorem can be applied to the mapping $v \mapsto u ( v )$ to solve the equation (a6). The result has been applied to quasi-linear parabolic partial differential equations with quasi-linear boundary conditions.
References
| [a1] | P. Acquistapace, "Evolution operators and strong solutions of abstract linear parabolic equations" Diff. and Integral Eq. , 1 (1988) pp. 433–457 |
| [a2] | P. Acquistapace, B. Terreni, "Some existence and regularity results for abstract non-autonomous parabolic equations" J. Math. Anal. Appl. , 99 (1984) pp. 9–64 |
| [a3] | P. Acquistapace, B. Terreni, "On fundamental solutions for abstract parabolic equations" A. Favini (ed.) E. Obrecht (ed.) , Differential Equations in Banach Spaces, Bologna, 1985 , Lecture Notes Math. , 1223 , Springer (1986) pp. 1–11 |
| [a4] | P. Acquistapace, B. Terreni, "A unified approach to abstract linear non-autonomous parabolic equations" Rend. Sem. Univ. Padova , 78 (1987) pp. 47–107 |
| [a5] | H. Amann, "Quasilinear parabolic systems under nonlinear boundary conditions" Arch. Rat. Mech. Anal. , 92 (1986) pp. 153–192 |
| [a6] | H. Amann, "On abstract parabolic fundamental solutions" J. Math. Soc. Japan , 39 (1987) pp. 93–116 |
| [a7] | H. Amann, "Linear and quasilinear parabolic problems I: Abstract linear theory" , Monogr. Math. , 89 , Birkhäuser (1995) |
| [a8] | T. Kato, H. Tanabe, "On the abstract evolution equation" Osaka Math. J. , 14 (1962) pp. 107–133 |
| [a9] | A. Lunardi, "Analytic semigroups and optimal regularity in parabolic problems" , Progr. Nonlinear Diff. Eqns. Appl. , 16 , Birkhäuser (1995) |
| [a10] | A. Yagi, "On the abstract evolution equation of parablic type" Osaka J. Math. , 14 (1977) pp. 557–568 |
Abstract parabolic differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abstract_parabolic_differential_equation&oldid=11870