Difference between revisions of "Illative combinatory logic"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[Combinatory logic|Combinatory logic]], which began with a paper by M. Schönfinkel [[#References|[a13]]], was developed by H.B. Curry and others with the intention of providing an alternative foundation for mathematics. Curry's theory is divided into two parts: pure combinatory logic ( | + | <!-- |
| + | i1100601.png | ||
| + | $#A+1 = 109 n = 1 | ||
| + | $#C+1 = 109 : ~/encyclopedia/old_files/data/I110/I.1100060 Illative combinatory logic | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | [[Combinatory logic|Combinatory logic]], which began with a paper by M. Schönfinkel [[#References|[a13]]], was developed by H.B. Curry and others with the intention of providing an alternative foundation for mathematics. Curry's theory is divided into two parts: pure combinatory logic ( $ { \mathop{\rm CL} } $), | ||
| + | concerning itself with notions like substitution and other (formula) manipulations; and illative combinatory logic ( $ { \mathop{\rm ICL} } $), | ||
| + | concerning itself with logical notions such as implication, quantification, equality, and types. In pure combinatory logic there is a set of terms built by application from variables and two constants $ \mathbf K $ | ||
| + | and $ \mathbf S $, | ||
| + | and there are two conversion rules: $ ( \mathbf K x ) y = x $ | ||
| + | and $ ( ( \mathbf S x ) y ) z = ( xz ) ( yz ) $. | ||
| + | In the presence of the rule of extensionality, the theory $ { \mathop{\rm CL} } $ | ||
| + | is equivalent with untyped lambda-calculus (cf. also [[Lambda-calculus| $ \lambda $- | ||
| + | calculus]]) with $ \beta \eta $- | ||
| + | conversion. $ { \mathop{\rm ICL} } $ | ||
| + | contains all of $ { \mathop{\rm CL} } $, | ||
| + | but the alphabet is extended by extra logical constants, and there are derivation rules capturing the intended meaning of these constants. | ||
Also, in the early papers [[#References|[a14]]], [[#References|[a15]]], A. Church attempted to form a single foundation for the whole of logic by a complicated combination of lambda-calculus and illative notions. But in [[#References|[a12]]], S.C. Kleene and J.B. Rosser proved that this system was inconsistent. This proof involved Gödelization (cf. also [[Arithmetization|Arithmetization]]), and with all the relevant details took sixty pages. Church and his students then abandoned the study of illative combinatory logic. | Also, in the early papers [[#References|[a14]]], [[#References|[a15]]], A. Church attempted to form a single foundation for the whole of logic by a complicated combination of lambda-calculus and illative notions. But in [[#References|[a12]]], S.C. Kleene and J.B. Rosser proved that this system was inconsistent. This proof involved Gödelization (cf. also [[Arithmetization|Arithmetization]]), and with all the relevant details took sixty pages. Church and his students then abandoned the study of illative combinatory logic. | ||
| − | ==An | + | ==An $ { \mathop{\rm ICL} } $-system of Curry.== |
| − | The following system, | + | The following system, $ {\mathcal I} $, |
| + | due essentially to Curry, is an early and simple example of an $ { \mathop{\rm ICL} } $- | ||
| + | system. | ||
| − | i) The set of terms of | + | i) The set of terms of $ {\mathcal I} $ |
| + | is built, by application, from the terms of $ { \mathop{\rm CL} } $ | ||
| + | plus the extra constant $ \Xi $. | ||
| − | ii) A statement of | + | ii) A statement of $ {\mathcal I} $ |
| + | is just a term. A basis is a set of statements. | ||
| − | iii) Let | + | iii) Let $ \Gamma $ |
| + | be a basis and $ X $ | ||
| + | a statement; then $ X $ | ||
| + | is derivable from $ \Gamma $, | ||
| + | denoted by $ \Gamma \vdash X $, | ||
| + | if $ \Gamma \vdash X $ | ||
| + | can be produced by the following natural deduction system: | ||
| − | + | $$ | |
| + | X \in \Gamma \Rightarrow \Gamma \vdash X, | ||
| + | $$ | ||
| − | + | $$ | |
| + | \Gamma \vdash X X = Y \Rightarrow \Gamma \vdash Y, | ||
| + | $$ | ||
| − | + | $$ | |
| + | \Gamma \vdash \Xi XY \Gamma \vdash XZ \Rightarrow \Gamma \vdash YZ, | ||
| + | $$ | ||
| − | + | $$ | |
| + | \Gamma, Xx \vdash Yx, x \notin { \mathop{\rm FV} } ( \Gamma,X,Y ) \Rightarrow \Gamma \vdash \Xi XY. | ||
| + | $$ | ||
| − | Here, | + | Here, $ = $ |
| + | stands for $ \beta \eta $- | ||
| + | equality, $ XZ $ | ||
| + | may be interpreted as $ Z \in X $, | ||
| + | and the intended meaning of $ \Xi $ | ||
| + | is $ \subset $, | ||
| + | so that the intuition behind the rule $ \Gamma \vdash \Xi XY $, | ||
| + | $ \Gamma \vdash XZ \Rightarrow \Gamma \vdash YZ $ | ||
| + | is: $ X \subset Y $, | ||
| + | $ Z \in X \Rightarrow Z \in Y $. | ||
| − | For terms | + | For terms $ X $, |
| + | $ Y $ | ||
| + | write: $ X \supset Y \equiv \Xi ( \mathbf K X ) ( \mathbf K Y ) $ | ||
| + | and $ \forall u \in X.Y \equiv \Xi X ( \lambda u.Y ) $. | ||
| + | Then the definition of $ {\mathcal I} $ | ||
| + | immediately implies: | ||
| − | i) | + | i) $ \Gamma \vdash X \supset Y $, |
| + | $ \Gamma \vdash X \Rightarrow \Gamma \vdash Y $. | ||
| − | ii) | + | ii) $ \Gamma,X \vdash Y \Rightarrow \Gamma \vdash X \supset Y $. |
| − | iii) | + | iii) $ \Gamma \vdash \forall u \in X.Y $, |
| + | $ \Gamma \vdash Xt \Rightarrow \Gamma \vdash Y [ u : = t ] $. | ||
| − | iv) | + | iv) $ \Gamma,Xu \vdash Y $, |
| + | $ u \notin { \mathop{\rm FV} } ( \Gamma,X ) \Rightarrow \Gamma \vdash \forall u \in X.Y $. | ||
| + | Now it is possible to interpret the $ \{ \supset , \forall \} $ | ||
| + | fragment of first-order intuitionistic predicate logic into $ {\mathcal I} $( | ||
| + | cf. also [[Interpretation|Interpretation]]). For example, a sentence like $ \forall x ( Rx \supset Rx ) $, | ||
| + | holding in a universe $ A $, | ||
| + | is translated as the statement $ ( \forall x \in A.Rx \supset Rx ) $, | ||
| + | which is $ \Xi A ( \lambda x. \Xi ( \mathbf K ( Rx ) ) ( \mathbf K ( Rx ) ) ) $, | ||
| + | and is provable in $ {\mathcal I} $. | ||
| − | Unfortunately, the interpretation is not complete because the system | + | Unfortunately, the interpretation is not complete because the system $ {\mathcal I} $ |
| + | is also inconsistent (cf. also [[Completeness (in logic)|Completeness (in logic)]]; [[Inconsistency|Inconsistency]]): every statement $ X $( | ||
| + | i.e., every term) can be derived in $ {\mathcal I} $( | ||
| + | from the empty basis). This already followed from the paper [[#References|[a12]]], involving Gödelization, but a much easier proof, essentially given in [[#References|[a7]]], is as follows. Let $ X $ | ||
| + | be given. Take $ Y \equiv ( \lambda y. ( yy ) \supset X ) ( \lambda y. ( yy ) \supset X ) $. | ||
| + | Then $ Y = Y \supset X $. | ||
| + | So, | ||
| − | + | $$ | |
| + | Y \vdash Y \Rightarrow Y \vdash Y \supset X \Rightarrow Y \vdash X \Rightarrow | ||
| + | $$ | ||
| − | + | $$ | |
| + | \Rightarrow | ||
| + | { } \vdash Y \supset X \Rightarrow { } \vdash Y \Rightarrow \vdash X . | ||
| + | $$ | ||
Curry and his school then defined weaker systems which were still strong enough to interpret logic, but the consistency of these systems remained an open question; cf. [[#References|[a6]]], [[#References|[a2]]], [[#References|[a3]]], [[#References|[a4]]]. | Curry and his school then defined weaker systems which were still strong enough to interpret logic, but the consistency of these systems remained an open question; cf. [[#References|[a6]]], [[#References|[a2]]], [[#References|[a3]]], [[#References|[a4]]]. | ||
| − | ==A consistent | + | ==A consistent $ { \mathop{\rm ICL} } $-system.== |
| − | The essential step in the inconsistency proof above is | + | The essential step in the inconsistency proof above is $ Y \vdash X \Rightarrow { } \vdash Y \supset X $. |
| + | This should hold only for "formulas" $ X $ | ||
| + | and $ Y $. | ||
| + | This is taken into account in the system $ {\mathcal I} \Xi $ | ||
| + | defined from $ {\mathcal I} $ | ||
| + | as follows. Let $ \mathbf L $ | ||
| + | be an extra constant and write $ \mathbf H \equiv \mathbf L \circ \mathbf K $. | ||
| + | (The intended meaning of $ \mathbf L X $ | ||
| + | is: $ X $ | ||
| + | is a set, and for $ \mathbf H X $ | ||
| + | it is: $ X $ | ||
| + | is a proposition.) Now add in the $ \Xi $- | ||
| + | introduction rule for $ {\mathcal I} $ | ||
| + | the extra condition $ \mathbf L X $ | ||
| + | and add an extra rule: | ||
| − | + | $$ | |
| + | \Gamma,Xx \vdash | ||
| + | \mathbf H ( Yx ) , \Gamma \vdash \mathbf L X , x \notin { \mathop{\rm FV} } ( \Gamma,X,Y ) \Rightarrow | ||
| + | $$ | ||
| − | + | $$ | |
| + | \Rightarrow | ||
| + | \Gamma \vdash \mathbf H ( \Xi XY ) . | ||
| + | $$ | ||
| − | The resulting system | + | The resulting system $ {\mathcal I} \Xi $ |
| + | is consistent and the obvious interpretation of the $ \{ \supset , \forall \} $ | ||
| + | fragment of first-order intuitionistic predicate logic into $ {\mathcal I} \Xi $ | ||
| + | is sound (cf. [[Completeness (in logic)|Completeness (in logic)]]), and, moreover, complete; cf. [[#References|[a1]]]. | ||
| − | ==Other | + | ==Other $ { \mathop{\rm ICL} } $-systems.== |
| − | Similarly one has systems | + | Similarly one has systems $ {\mathcal I} \mathbf P $, |
| + | $ {\mathcal I} \mathbf F $ | ||
| + | and $ {\mathcal I} \mathbf G $, | ||
| + | where one has, instead of $ \Xi $, | ||
| + | extra constants $ \mathbf P $, | ||
| + | $ \mathbf F $ | ||
| + | and $ \mathbf G $, | ||
| + | respectively. The intended interpretation of these constants is as follows. $ \mathbf P XY $ | ||
| + | is $ X \supset Y $, | ||
| + | $ \mathbf F XY $ | ||
| + | is $ Y ^ {X} $, | ||
| + | and $ \mathbf G XY $ | ||
| + | is $ \forall x \in X.Y x $. | ||
| + | First-order intuitionistic proposition logic $ { \mathop{\rm PROP} } $ | ||
| + | and predicate logic $ { \mathop{\rm PRED} } $ | ||
| + | can be interpreted in $ { \mathop{\rm ICL} } $- | ||
| + | systems in two ways: following the propositions-as-types paradigm, in which derivations become combinators, or in a more direct way, in which derivations are not translated. Here, $ { \mathop{\rm PROP} } $ | ||
| + | is interpreted in $ {\mathcal I} \mathbf P $ | ||
| + | and $ {\mathcal I} \mathbf F $ | ||
| + | and $ { \mathop{\rm PRED} } $ | ||
| + | in $ {\mathcal I} \Xi $ | ||
| + | and $ {\mathcal I} \mathbf G $. | ||
| + | In [[#References|[a1]]] and [[#References|[a10]]] it is proved that all four interpretations are sound and complete. This fulfills, after sixty years, the programme of Church and Curry to base logic on a consistent system of $ \lambda $- | ||
| + | terms or combinators. Extensions to deal with higher-order notions and type theories are being studied. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Barendregt, M. Bunder, W. Dekkers, "Systems of illative combinatory logic complete for first-order propositional and predicate calculus" ''J. Symb. Logic'' , '''58''' (1993) pp. 769–888</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M.W. Bunder, "Set theory based on combinatory logic" ''Ph.D. Thesis UvA Amsterdam'' (1969)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M.W. Bunder, "A deduction theorem for restricted generality" ''Notre Dame J. Formal Logic'' , '''14''' (1973) pp. 341–346</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M.W. Bunder, "Propositional and predicate calculus based on combinatory logic" ''Notre Dame J. Formal Logic'' , '''15''' (1974) pp. 25–32</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H.B. Curry, "Grundlagen der kombinatorischen Logik. Inauguraldissertation" ''Amer. J. Math.'' , '''52''' (1930) pp. 509–536; 789–834</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H.B. Curry, "Some advances in the combinatory theory of quantification" ''Proc. Nat. Acad. Sci. USA'' , '''28''' (1942) pp. 564–569</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H.B. Curry, "The inconsistency of certain formal logics" ''J. Symb. Logic'' , '''7''' (1942) pp. 115–117</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> H.B. Curry, R. Feys, "Combinatory logic" , '''1''' , North-Holland (1958)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> H.B. Curry, J.R. Hindley, J.P. Seldin, "Combinatory logic" , '''2''' , North-Holland (1972)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> W. Dekkers, M. Bunder, H. Barendregt, "Completeness of the propositions-as-types interpretation of intuitionistic logic into illative combinatory logic" ''J. Symbolic Logic'' (to appear)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> J.R. Hindley, J.P. Seldin, "Introduction to combinators and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i110/i110060/i110060120.png" />-calculus" , Cambridge Univ. Press (1986)</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> S.C. Kleene, J.B. Rosser, "The inconsistency of certain formal logics" ''Ann. of Math. (2)'' , '''36''' (1935) pp. 630–636</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> M. Schönfinkel, "Über die Bausteine | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Barendregt, M. Bunder, W. Dekkers, "Systems of illative combinatory logic complete for first-order propositional and predicate calculus" ''J. Symb. Logic'' , '''58''' (1993) pp. 769–888</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M.W. Bunder, "Set theory based on combinatory logic" ''Ph.D. Thesis UvA Amsterdam'' (1969)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M.W. Bunder, "A deduction theorem for restricted generality" ''Notre Dame J. Formal Logic'' , '''14''' (1973) pp. 341–346</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M.W. Bunder, "Propositional and predicate calculus based on combinatory logic" ''Notre Dame J. Formal Logic'' , '''15''' (1974) pp. 25–32</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H.B. Curry, "Grundlagen der kombinatorischen Logik. Inauguraldissertation" ''Amer. J. Math.'' , '''52''' (1930) pp. 509–536; 789–834</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H.B. Curry, "Some advances in the combinatory theory of quantification" ''Proc. Nat. Acad. Sci. USA'' , '''28''' (1942) pp. 564–569</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H.B. Curry, "The inconsistency of certain formal logics" ''J. Symb. Logic'' , '''7''' (1942) pp. 115–117</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> H.B. Curry, R. Feys, "Combinatory logic" , '''1''' , North-Holland (1958)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> H.B. Curry, J.R. Hindley, J.P. Seldin, "Combinatory logic" , '''2''' , North-Holland (1972)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> W. Dekkers, M. Bunder, H. Barendregt, "Completeness of the propositions-as-types interpretation of intuitionistic logic into illative combinatory logic" ''J. Symbolic Logic'' (to appear)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> J.R. Hindley, J.P. Seldin, "Introduction to combinators and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i110/i110060/i110060120.png" />-calculus" , Cambridge Univ. Press (1986)</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> S.C. Kleene, J.B. Rosser, "The inconsistency of certain formal logics" ''Ann. of Math. (2)'' , '''36''' (1935) pp. 630–636</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> M. Schönfinkel, "Über die Bausteine der mathematischen Logik" ''Math. Ann.'' , '''92''' (1924) pp. 305–316</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> A. Church, "A set of postulates for the foundation of logic" ''Ann. of Math. (2)'' , '''33''' (1932) pp. 346–366</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> A. Church, "A set of postulates for the foundation of logic" ''Ann. of Math. (2)'' , '''34''' (1933) pp. 839–864</TD></TR></table> |
Latest revision as of 22:11, 5 June 2020
Combinatory logic, which began with a paper by M. Schönfinkel [a13], was developed by H.B. Curry and others with the intention of providing an alternative foundation for mathematics. Curry's theory is divided into two parts: pure combinatory logic ( $ { \mathop{\rm CL} } $),
concerning itself with notions like substitution and other (formula) manipulations; and illative combinatory logic ( $ { \mathop{\rm ICL} } $),
concerning itself with logical notions such as implication, quantification, equality, and types. In pure combinatory logic there is a set of terms built by application from variables and two constants $ \mathbf K $
and $ \mathbf S $,
and there are two conversion rules: $ ( \mathbf K x ) y = x $
and $ ( ( \mathbf S x ) y ) z = ( xz ) ( yz ) $.
In the presence of the rule of extensionality, the theory $ { \mathop{\rm CL} } $
is equivalent with untyped lambda-calculus (cf. also $ \lambda $-
calculus) with $ \beta \eta $-
conversion. $ { \mathop{\rm ICL} } $
contains all of $ { \mathop{\rm CL} } $,
but the alphabet is extended by extra logical constants, and there are derivation rules capturing the intended meaning of these constants.
Also, in the early papers [a14], [a15], A. Church attempted to form a single foundation for the whole of logic by a complicated combination of lambda-calculus and illative notions. But in [a12], S.C. Kleene and J.B. Rosser proved that this system was inconsistent. This proof involved Gödelization (cf. also Arithmetization), and with all the relevant details took sixty pages. Church and his students then abandoned the study of illative combinatory logic.
An $ { \mathop{\rm ICL} } $-system of Curry.
The following system, $ {\mathcal I} $, due essentially to Curry, is an early and simple example of an $ { \mathop{\rm ICL} } $- system.
i) The set of terms of $ {\mathcal I} $ is built, by application, from the terms of $ { \mathop{\rm CL} } $ plus the extra constant $ \Xi $.
ii) A statement of $ {\mathcal I} $ is just a term. A basis is a set of statements.
iii) Let $ \Gamma $ be a basis and $ X $ a statement; then $ X $ is derivable from $ \Gamma $, denoted by $ \Gamma \vdash X $, if $ \Gamma \vdash X $ can be produced by the following natural deduction system:
$$ X \in \Gamma \Rightarrow \Gamma \vdash X, $$
$$ \Gamma \vdash X X = Y \Rightarrow \Gamma \vdash Y, $$
$$ \Gamma \vdash \Xi XY \Gamma \vdash XZ \Rightarrow \Gamma \vdash YZ, $$
$$ \Gamma, Xx \vdash Yx, x \notin { \mathop{\rm FV} } ( \Gamma,X,Y ) \Rightarrow \Gamma \vdash \Xi XY. $$
Here, $ = $ stands for $ \beta \eta $- equality, $ XZ $ may be interpreted as $ Z \in X $, and the intended meaning of $ \Xi $ is $ \subset $, so that the intuition behind the rule $ \Gamma \vdash \Xi XY $, $ \Gamma \vdash XZ \Rightarrow \Gamma \vdash YZ $ is: $ X \subset Y $, $ Z \in X \Rightarrow Z \in Y $.
For terms $ X $, $ Y $ write: $ X \supset Y \equiv \Xi ( \mathbf K X ) ( \mathbf K Y ) $ and $ \forall u \in X.Y \equiv \Xi X ( \lambda u.Y ) $. Then the definition of $ {\mathcal I} $ immediately implies:
i) $ \Gamma \vdash X \supset Y $, $ \Gamma \vdash X \Rightarrow \Gamma \vdash Y $.
ii) $ \Gamma,X \vdash Y \Rightarrow \Gamma \vdash X \supset Y $.
iii) $ \Gamma \vdash \forall u \in X.Y $, $ \Gamma \vdash Xt \Rightarrow \Gamma \vdash Y [ u : = t ] $.
iv) $ \Gamma,Xu \vdash Y $, $ u \notin { \mathop{\rm FV} } ( \Gamma,X ) \Rightarrow \Gamma \vdash \forall u \in X.Y $. Now it is possible to interpret the $ \{ \supset , \forall \} $ fragment of first-order intuitionistic predicate logic into $ {\mathcal I} $( cf. also Interpretation). For example, a sentence like $ \forall x ( Rx \supset Rx ) $, holding in a universe $ A $, is translated as the statement $ ( \forall x \in A.Rx \supset Rx ) $, which is $ \Xi A ( \lambda x. \Xi ( \mathbf K ( Rx ) ) ( \mathbf K ( Rx ) ) ) $, and is provable in $ {\mathcal I} $.
Unfortunately, the interpretation is not complete because the system $ {\mathcal I} $ is also inconsistent (cf. also Completeness (in logic); Inconsistency): every statement $ X $( i.e., every term) can be derived in $ {\mathcal I} $( from the empty basis). This already followed from the paper [a12], involving Gödelization, but a much easier proof, essentially given in [a7], is as follows. Let $ X $ be given. Take $ Y \equiv ( \lambda y. ( yy ) \supset X ) ( \lambda y. ( yy ) \supset X ) $. Then $ Y = Y \supset X $. So,
$$ Y \vdash Y \Rightarrow Y \vdash Y \supset X \Rightarrow Y \vdash X \Rightarrow $$
$$ \Rightarrow { } \vdash Y \supset X \Rightarrow { } \vdash Y \Rightarrow \vdash X . $$
Curry and his school then defined weaker systems which were still strong enough to interpret logic, but the consistency of these systems remained an open question; cf. [a6], [a2], [a3], [a4].
A consistent $ { \mathop{\rm ICL} } $-system.
The essential step in the inconsistency proof above is $ Y \vdash X \Rightarrow { } \vdash Y \supset X $. This should hold only for "formulas" $ X $ and $ Y $. This is taken into account in the system $ {\mathcal I} \Xi $ defined from $ {\mathcal I} $ as follows. Let $ \mathbf L $ be an extra constant and write $ \mathbf H \equiv \mathbf L \circ \mathbf K $. (The intended meaning of $ \mathbf L X $ is: $ X $ is a set, and for $ \mathbf H X $ it is: $ X $ is a proposition.) Now add in the $ \Xi $- introduction rule for $ {\mathcal I} $ the extra condition $ \mathbf L X $ and add an extra rule:
$$ \Gamma,Xx \vdash \mathbf H ( Yx ) , \Gamma \vdash \mathbf L X , x \notin { \mathop{\rm FV} } ( \Gamma,X,Y ) \Rightarrow $$
$$ \Rightarrow \Gamma \vdash \mathbf H ( \Xi XY ) . $$
The resulting system $ {\mathcal I} \Xi $ is consistent and the obvious interpretation of the $ \{ \supset , \forall \} $ fragment of first-order intuitionistic predicate logic into $ {\mathcal I} \Xi $ is sound (cf. Completeness (in logic)), and, moreover, complete; cf. [a1].
Other $ { \mathop{\rm ICL} } $-systems.
Similarly one has systems $ {\mathcal I} \mathbf P $, $ {\mathcal I} \mathbf F $ and $ {\mathcal I} \mathbf G $, where one has, instead of $ \Xi $, extra constants $ \mathbf P $, $ \mathbf F $ and $ \mathbf G $, respectively. The intended interpretation of these constants is as follows. $ \mathbf P XY $ is $ X \supset Y $, $ \mathbf F XY $ is $ Y ^ {X} $, and $ \mathbf G XY $ is $ \forall x \in X.Y x $. First-order intuitionistic proposition logic $ { \mathop{\rm PROP} } $ and predicate logic $ { \mathop{\rm PRED} } $ can be interpreted in $ { \mathop{\rm ICL} } $- systems in two ways: following the propositions-as-types paradigm, in which derivations become combinators, or in a more direct way, in which derivations are not translated. Here, $ { \mathop{\rm PROP} } $ is interpreted in $ {\mathcal I} \mathbf P $ and $ {\mathcal I} \mathbf F $ and $ { \mathop{\rm PRED} } $ in $ {\mathcal I} \Xi $ and $ {\mathcal I} \mathbf G $. In [a1] and [a10] it is proved that all four interpretations are sound and complete. This fulfills, after sixty years, the programme of Church and Curry to base logic on a consistent system of $ \lambda $- terms or combinators. Extensions to deal with higher-order notions and type theories are being studied.
References
| [a1] | H. Barendregt, M. Bunder, W. Dekkers, "Systems of illative combinatory logic complete for first-order propositional and predicate calculus" J. Symb. Logic , 58 (1993) pp. 769–888 |
| [a2] | M.W. Bunder, "Set theory based on combinatory logic" Ph.D. Thesis UvA Amsterdam (1969) |
| [a3] | M.W. Bunder, "A deduction theorem for restricted generality" Notre Dame J. Formal Logic , 14 (1973) pp. 341–346 |
| [a4] | M.W. Bunder, "Propositional and predicate calculus based on combinatory logic" Notre Dame J. Formal Logic , 15 (1974) pp. 25–32 |
| [a5] | H.B. Curry, "Grundlagen der kombinatorischen Logik. Inauguraldissertation" Amer. J. Math. , 52 (1930) pp. 509–536; 789–834 |
| [a6] | H.B. Curry, "Some advances in the combinatory theory of quantification" Proc. Nat. Acad. Sci. USA , 28 (1942) pp. 564–569 |
| [a7] | H.B. Curry, "The inconsistency of certain formal logics" J. Symb. Logic , 7 (1942) pp. 115–117 |
| [a8] | H.B. Curry, R. Feys, "Combinatory logic" , 1 , North-Holland (1958) |
| [a9] | H.B. Curry, J.R. Hindley, J.P. Seldin, "Combinatory logic" , 2 , North-Holland (1972) |
| [a10] | W. Dekkers, M. Bunder, H. Barendregt, "Completeness of the propositions-as-types interpretation of intuitionistic logic into illative combinatory logic" J. Symbolic Logic (to appear) |
| [a11] | J.R. Hindley, J.P. Seldin, "Introduction to combinators and 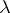 -calculus" , Cambridge Univ. Press (1986) -calculus" , Cambridge Univ. Press (1986) |
| [a12] | S.C. Kleene, J.B. Rosser, "The inconsistency of certain formal logics" Ann. of Math. (2) , 36 (1935) pp. 630–636 |
| [a13] | M. Schönfinkel, "Über die Bausteine der mathematischen Logik" Math. Ann. , 92 (1924) pp. 305–316 |
| [a14] | A. Church, "A set of postulates for the foundation of logic" Ann. of Math. (2) , 33 (1932) pp. 346–366 |
| [a15] | A. Church, "A set of postulates for the foundation of logic" Ann. of Math. (2) , 34 (1933) pp. 839–864 |
Illative combinatory logic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Illative_combinatory_logic&oldid=11313