Difference between revisions of "Breaking point"
From Encyclopedia of Mathematics
(Importing text file) |
m (image svg) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
''angle point'' | ''angle point'' | ||
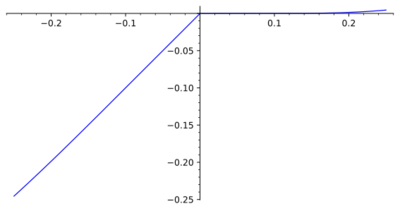
| − | A singular point of a plane curve with the property that two branches of the curve end in it in such a way that each has a (one-sided) tangent at the point different from the other. For example, the origin is a breaking point of the curve | + | A singular point of a plane curve with the property that two branches of the curve end in it in such a way that each has a (one-sided) tangent at the point different from the other. For example, the origin is a breaking point of the curve $y=x/(1+e^{1/x})$ (see Fig.). The left and right derivatives are different at a breaking point. |
| − | + | [[File:Breaking point example.svg|center|400px]] | |
| − | |||
| − | |||
Latest revision as of 15:05, 23 July 2025
angle point
A singular point of a plane curve with the property that two branches of the curve end in it in such a way that each has a (one-sided) tangent at the point different from the other. For example, the origin is a breaking point of the curve $y=x/(1+e^{1/x})$ (see Fig.). The left and right derivatives are different at a breaking point.
How to Cite This Entry:
Breaking point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Breaking_point&oldid=15172
Breaking point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Breaking_point&oldid=15172
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article