Difference between revisions of "Varignon parallelogram"
From Encyclopedia of Mathematics
m (→References: isbn link) |
(image) |
||
| Line 1: | Line 1: | ||
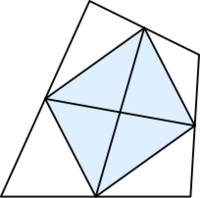
Take an arbitrary quadrangle and take the midpoints of each of the four sides. Join adjoining midpoints. The result is a parallelogram, called the Varignon parallelogram. This theorem is due to P. Varignon (around 1700). The assertion that the bimedians (i.e. the lines joining opposite midpoints) bisect each other is equivalent to it. | Take an arbitrary quadrangle and take the midpoints of each of the four sides. Join adjoining midpoints. The result is a parallelogram, called the Varignon parallelogram. This theorem is due to P. Varignon (around 1700). The assertion that the bimedians (i.e. the lines joining opposite midpoints) bisect each other is equivalent to it. | ||
| − | + | [[File:Varignon parallelogramme.svg|center|200px]] | |
| − | |||
| − | |||
The centre of mass of the Varignon parallelogram is the centroid of the original quadrangle (the centre of mass of four equal masses placed at the four vertices). | The centre of mass of the Varignon parallelogram is the centroid of the original quadrangle (the centre of mass of four equal masses placed at the four vertices). | ||
| − | A different [[ | + | A different [[Varignon theorem]] deals with sliding vectors. |
====References==== | ====References==== | ||
<table> | <table> | ||
| − | <TR><TD valign="top">[a1]</TD> <TD valign="top"> H.S.M. Coxeter, | + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> H.S.M. Coxeter, "Introduction to geometry" (2nd ed.), Wiley (1969) pp. 199 {{ZBL|0181.48101}}; (repr.1989) {{ISBN|0-471-50458-0}}</TD></TR> |
| − | <TR><TD valign="top">[a2]</TD> <TD valign="top"> H.S.M. Coxeter, | + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> H.S.M. Coxeter, S.L. Greitzer, "Geometry revisited" , Math. Assoc. America (1967) pp. 51–56 {{ZBL|0166.16402}}</TD></TR> |
</table> | </table> | ||
| − | |||
| − | |||
Latest revision as of 13:02, 18 July 2025
Take an arbitrary quadrangle and take the midpoints of each of the four sides. Join adjoining midpoints. The result is a parallelogram, called the Varignon parallelogram. This theorem is due to P. Varignon (around 1700). The assertion that the bimedians (i.e. the lines joining opposite midpoints) bisect each other is equivalent to it.
The centre of mass of the Varignon parallelogram is the centroid of the original quadrangle (the centre of mass of four equal masses placed at the four vertices).
A different Varignon theorem deals with sliding vectors.
References
| [a1] | H.S.M. Coxeter, "Introduction to geometry" (2nd ed.), Wiley (1969) pp. 199 Zbl 0181.48101; (repr.1989) ISBN 0-471-50458-0 |
| [a2] | H.S.M. Coxeter, S.L. Greitzer, "Geometry revisited" , Math. Assoc. America (1967) pp. 51–56 Zbl 0166.16402 |
How to Cite This Entry:
Varignon parallelogram. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Varignon_parallelogram&oldid=54640
Varignon parallelogram. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Varignon_parallelogram&oldid=54640
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article