Difference between revisions of "Steiner curve"
From Encyclopedia of Mathematics
(TeX) |
m (OldImage template added) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 19: | Line 19: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Steiner, "Werke" , '''1–2''' , Springer (1880–1882)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Steiner, "Werke" , '''1–2''' , Springer (1880–1882)</TD></TR> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Berger, "Geometry" , '''1–2''' , Springer (1987) pp. §9.14.34 (Translated from French)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> F. Gomes Teixeira, "Traité des courbes" , '''1–3''' , Chelsea, reprint (1971)</TD></TR></table> | ||
| − | + | {{OldImage}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 18:08, 19 April 2024
A plane algebraic curve of order four, described by the point on a circle of radius $r$ rolling upon a circle of radius $R=3r$ and having with it internal tangency; a hypocycloid with modulus $m=3$. A Steiner curve is expressed by the following equation in rectangular Cartesian coordinates:
$$(x^2+y^2)^2+8rx(3y^2-x^2)+18r^2(x^2+y^2)-27r^4=0.$$
A Steiner curve has three cusps (see Fig. a).
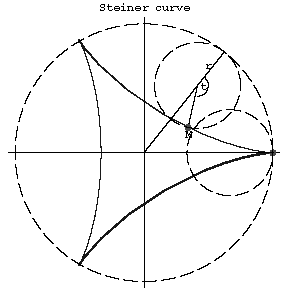
Figure: s087650a
The length of the arc from the point $A$ is:
$$l=\frac{16}{3}r\sin^2\frac t4.$$
The length of the entire curve is $16r$. The radius of curvature is $r_k=8\sin(t/2)$. The area bounded by the curve is $S=2\pi r^2$.
This curve was studied by Jacob Steiner (1798–1863).
References
| [1] | J. Steiner, "Werke" , 1–2 , Springer (1880–1882) |
| [a1] | M. Berger, "Geometry" , 1–2 , Springer (1987) pp. §9.14.34 (Translated from French) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
How to Cite This Entry:
Steiner curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steiner_curve&oldid=31569
Steiner curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steiner_curve&oldid=31569
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article