Difference between revisions of "BBGKY hierarchy"
(Importing text file) |
(latex details) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 54 formulas, 48 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
''Bogolyubov–Born–Green–Kirkwood–Yvon hierarchy'' | ''Bogolyubov–Born–Green–Kirkwood–Yvon hierarchy'' | ||
A chain of an infinite number of integro-differential evolution equations for the sequence of distribution (correlation) functions describing all possible states of a many-particle system. For systems of finitely many particles the BBGKY hierarchy is equivalent to the [[Liouville-equation(2)|Liouville equation]] in the classical case and to the von Neumann equation in the quantum case. | A chain of an infinite number of integro-differential evolution equations for the sequence of distribution (correlation) functions describing all possible states of a many-particle system. For systems of finitely many particles the BBGKY hierarchy is equivalent to the [[Liouville-equation(2)|Liouville equation]] in the classical case and to the von Neumann equation in the quantum case. | ||
| − | Let | + | Let $F ( t ) = ( F _ { 1 } ( t , x _ { 1 } ) , \ldots , F _ { n } ( t , x _ { 1 } , \ldots , x _ { n } ) , \ldots )$ be a sequence of probability distribution functions $F _ { n } ( t )$ defined on the phase space of a system of $n$ particles $x _ { i } \equiv ( q _ { i } , p _ { i } ) \in \mathbf{R} ^ { \nu } \times \mathbf{R} ^ { \nu }$, $\nu \geq 1$ (cf. also [[Distribution function|Distribution function]]). The BBGKY hierarchy for classical systems reads as follows: |
| − | + | \begin{equation*} \frac { d } { d t } F ( t ) = - \mathcal{L} F ( t ) + [ \mathcal{L} , A ] F ( t ), \end{equation*} | |
| − | where the Liouville operator | + | where the Liouville operator $\mathcal{L}$ is defined by the [[Poisson brackets|Poisson brackets]] ($X \equiv ( x _ { 1 } , \dots , x _ { n } )$): |
| − | + | \begin{equation*} ( \mathcal{L} F ) _ { n } ( X ) = \{ H _ { n } , F _ { n } ( X ) \} \end{equation*} | |
| − | with [[Hamiltonian|Hamiltonian]] | + | with [[Hamiltonian|Hamiltonian]] $H _ { n } = \sum _ { i = 1 } ^ { n } p _ { i } ^ { 2 } / 2 + \sum _ { 1 = i < j } ^ { n } \Phi ( q _ { i } - q _ { j } )$ and the symbol $[ \cdot , \cdot ]$ denotes the commutator between the operator $\mathcal{L}$ and the operator |
| − | + | \begin{equation*} ( \mathcal{A} F ) _ { n } ( X ) = \int d x _ { n + 1} F _ { n + 1} ( X , x _ { n + 1} ). \end{equation*} | |
The main examples of the BBGKY hierarchy are discussed below [[#References|[a1]]]. | The main examples of the BBGKY hierarchy are discussed below [[#References|[a1]]]. | ||
| − | 1) For a smooth [[Potential|potential]] of interaction | + | 1) For a smooth [[Potential|potential]] of interaction $\Phi$, |
| − | + | \begin{equation*} ( [ {\cal L , A} ] F ) _ { n } ( X ) = \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120100/b12010016.png"/></td> </tr></table> |
2) For a system with singular potential of interaction | 2) For a system with singular potential of interaction | ||
| − | + | \begin{equation*} \Phi ( q ) = \left\{ \begin{array} { l l } { + \infty } & { \text { if } | q | \leq \sigma , } \\ { 0 } & { \text { if } | q | > \sigma , } \end{array} \right. \end{equation*} | |
| − | like a hard-sphere system of diameter | + | like a hard-sphere system of diameter $\sigma$, for dimension $\nu \geq 2$ at $t > 0$ one has |
| − | + | \begin{equation*} ( [ {\cal L , A} ] F ) _ { n } ( X ) = \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120100/b12010022.png"/></td> </tr></table> |
| − | + | \begin{equation*} - F _ { n + 1 } ( X , q _ { i } + \sigma \eta , p _ { n + 1 } ) ), \end{equation*} | |
| − | where | + | where $\langle \, .\, ,\, . \, \rangle$ is the inner product, |
| − | + | \begin{equation*} \mathcal{S} _ { + } ^ { \nu - 1 } = \left\{ \eta \in \mathbf{R} ^ { \nu } : | \eta | = 1 , \langle \eta , ( p _ { i } - p _ { n + 1 } ) \rangle > 0 \right\} \end{equation*} | |
and | and | ||
| − | + | \begin{equation*} p _ { i } ^ { * } = p _ { i } - \eta \langle \eta , ( p _ { i } - p _ { n + 1 } ) \rangle, \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120100/b12010027.png"/></td> </tr></table> |
3) The dual BBGKY hierarchy | 3) The dual BBGKY hierarchy | ||
| − | + | \begin{equation*} \frac { d } { d t } G ( t ) = \mathcal{L} G ( t ) + [ \mathcal{L} , \mathcal{A} ^ { * } ] G ( t ), \end{equation*} | |
| − | where | + | where $\mathcal{A} ^ { * }$ is the [[Adjoint operator|adjoint operator]] to $\mathcal{A}$: |
| − | + | \begin{equation*} ( \mathcal{A} ^ { * } f ) _ { n } ( X ) = \sum _ { i = 1 } ^ { n } f _ { n - 1 } ( x _ { 1 } , \dots , x _ { i - 1} , x _ { i + 1} , \dots , x _ { n } ). \end{equation*} | |
| − | Such a hierarchy describes the evolution of observables | + | Such a hierarchy describes the evolution of observables $G ( t )$ of a system of particle. |
There are two different approaches to constructing the solutions of the hierarchy: either by iteration or by a functional (cluster expansion) series; see [[#References|[a1]]]. The functional representation of the solution for the Cauchy problem depends on symmetry properties of the Hamiltonian and on initial distribution functions | There are two different approaches to constructing the solutions of the hierarchy: either by iteration or by a functional (cluster expansion) series; see [[#References|[a1]]]. The functional representation of the solution for the Cauchy problem depends on symmetry properties of the Hamiltonian and on initial distribution functions | ||
| − | + | \begin{equation*} F ( 0 ) = ( F _ { 1 } ( 0 , x _ { 1 } ) , \ldots , F _ { n } ( 0 , x _ { 1 } , \ldots , x _ { n } ) , \ldots ). \end{equation*} | |
In the symmetric case it has the form | In the symmetric case it has the form | ||
| − | + | \begin{equation*} F _ { s } ( t , x _ { 1 } , \ldots , x _ { s } ) = \end{equation*} | |
| − | + | \begin{equation*} = \sum _ { n = 0 } ^ { \infty } \int d x _ { s + 1} \cdots d x _ { s + n} U ^ { ( n )_t } F _ { s + n} ( 0 , x _ { 1 } , \dots , x _ { s + n} ), \end{equation*} | |
where | where | ||
| − | + | \begin{equation*} U ^ { ( n )_ t} = \sum _ { k = 0 } ^ { n } \frac { ( - 1 ) ^ { k } } { k ! ( n - k ) ! } S ^ { s + n - k } ( - t , x _ { 1 } , \dots , x _ { s + n - k} ) \end{equation*} | |
| − | and the evolution operator | + | and the evolution operator $S ^ { n } ( - t , x _ { 1 } , \dots , x _ { n } )$, |
| − | + | \begin{equation*} S ^ { n } ( - t , x _ { 1 } , \dots , x _ { n } ) F _ { n } ( x _ { 1 } , \dots , x _ { n } ) = \end{equation*} | |
| − | + | \begin{equation*} = F _ { n } ( X _ { 1 } ( - t , x _ { 1 } , \ldots , x _ { n } ) , \ldots , X _ { n } ( - t , x _ { 1 } , \ldots , x _ { n } ) ), \end{equation*} | |
| − | shifts the arguments of the functions along the solutions of the Hamilton equations (the phase trajectories) | + | shifts the arguments of the functions along the solutions of the Hamilton equations (the phase trajectories) $X _ { i } ( - t , x _ { 1 } , \ldots , x _ { n } )$, $i = 1 , \dots , n$, of a system of $n$ particles with initial data $X _ { i } ( 0 , x _ { i } ) = x _ { i }$. The evolution operators $S ^ { n } ( t )$ form a group of operators generated by the Liouville operator ${\cal L} _ { n }$ defined above. In certain cases this representation of the solution (a cluster expansion) can be treated as the solution $F ( t ) = U ( t ) F ( 0 )$ determined by a group of evolution operators $U ( t )$. In terms of the operators defined above, the group $U ( t )$ has the form |
| − | + | \begin{equation*} U ( t ) = e ^ { \mathcal{A} } S ( - t ) e ^ { - \mathcal{A} }. \end{equation*} | |
There exist various methods to give a meaning to the formal solution of the Cauchy problem to the BBGKY hierarchy in certain function spaces. For example, the semi-group method (in spaces of sequences of summable functions and, for quantum systems, in the space of sequences of kernel operators), the interaction region method (for constructing an a priori estimate of a solution), the thermodynamic limit method (for the time-continuation of the local solution in the space of sequences of bounded functions), and non-standard analysis methods. | There exist various methods to give a meaning to the formal solution of the Cauchy problem to the BBGKY hierarchy in certain function spaces. For example, the semi-group method (in spaces of sequences of summable functions and, for quantum systems, in the space of sequences of kernel operators), the interaction region method (for constructing an a priori estimate of a solution), the thermodynamic limit method (for the time-continuation of the local solution in the space of sequences of bounded functions), and non-standard analysis methods. | ||
| Line 83: | Line 91: | ||
To date (1998), existence and uniqueness results for the BBGKY hierarchy have been proved: | To date (1998), existence and uniqueness results for the BBGKY hierarchy have been proved: | ||
| − | a) in the space | + | a) in the space $L^1$ of sequences of summable functions (or kernel operators, in the quantum case): time-global solutions for general classes of an interaction potential; |
| − | b) in the space | + | b) in the space $L^{\infty}$ of sequences of functions bounded with respect to the configuration variables and decreasing with respect to the momentum variables: time-global solutions for the BBGKY hierarchy of a hard-sphere system for arbitrary initial data in the one-dimensional case and with initial data close to the equilibrium state in the many-dimensional case; also, time-global solutions for one-dimensional systems of particles interacting by the short-range potential with a hard-core and with initial data close to equilibrium. |
The BBGKY hierarchy allows one to describe both equilibrium and non-equilibrium states of many-particle systems from a common point of view. Non-equilibrium states are characterized by the solutions of the initial value problem for this hierarchy and, correspondingly, equilibrium states are characterized by the solutions of the steady BBGKY hierarchy, see [[#References|[a1]]], [[#References|[a3]]], [[#References|[a2]]]. | The BBGKY hierarchy allows one to describe both equilibrium and non-equilibrium states of many-particle systems from a common point of view. Non-equilibrium states are characterized by the solutions of the initial value problem for this hierarchy and, correspondingly, equilibrium states are characterized by the solutions of the steady BBGKY hierarchy, see [[#References|[a1]]], [[#References|[a3]]], [[#References|[a2]]]. | ||
| Line 94: | Line 102: | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table> |
| + | <tr><td valign="top">[a1]</td> <td valign="top"> C. Cercignani, V. Gerasimenko, D. Petrina, "Many-particle dynamics and kinetic equations" , Kluwer Acad. Publ. (1997)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> D. Petrina, V. Gerasimenko, P. Malyshev, "Mathematical foundations of classical statistical mechanics. Continuous systems" , Gordon&Breach (1989)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> D. Petrina, "Mathematical foundations of quantum statistical mechanics" , Kluwer Acad. Publ. (1995)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> C. Cercignani, R. Illner, M. Pulvirenti, "The mathematical theory of dilute gases" , Springer (1994)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> H. Spohn, "Large scale dynamics of interacting particles" , Springer (1991)</td></tr> | ||
| + | </table> | ||
Latest revision as of 07:38, 7 February 2024
Bogolyubov–Born–Green–Kirkwood–Yvon hierarchy
A chain of an infinite number of integro-differential evolution equations for the sequence of distribution (correlation) functions describing all possible states of a many-particle system. For systems of finitely many particles the BBGKY hierarchy is equivalent to the Liouville equation in the classical case and to the von Neumann equation in the quantum case.
Let $F ( t ) = ( F _ { 1 } ( t , x _ { 1 } ) , \ldots , F _ { n } ( t , x _ { 1 } , \ldots , x _ { n } ) , \ldots )$ be a sequence of probability distribution functions $F _ { n } ( t )$ defined on the phase space of a system of $n$ particles $x _ { i } \equiv ( q _ { i } , p _ { i } ) \in \mathbf{R} ^ { \nu } \times \mathbf{R} ^ { \nu }$, $\nu \geq 1$ (cf. also Distribution function). The BBGKY hierarchy for classical systems reads as follows:
\begin{equation*} \frac { d } { d t } F ( t ) = - \mathcal{L} F ( t ) + [ \mathcal{L} , A ] F ( t ), \end{equation*}
where the Liouville operator $\mathcal{L}$ is defined by the Poisson brackets ($X \equiv ( x _ { 1 } , \dots , x _ { n } )$):
\begin{equation*} ( \mathcal{L} F ) _ { n } ( X ) = \{ H _ { n } , F _ { n } ( X ) \} \end{equation*}
with Hamiltonian $H _ { n } = \sum _ { i = 1 } ^ { n } p _ { i } ^ { 2 } / 2 + \sum _ { 1 = i < j } ^ { n } \Phi ( q _ { i } - q _ { j } )$ and the symbol $[ \cdot , \cdot ]$ denotes the commutator between the operator $\mathcal{L}$ and the operator
\begin{equation*} ( \mathcal{A} F ) _ { n } ( X ) = \int d x _ { n + 1} F _ { n + 1} ( X , x _ { n + 1} ). \end{equation*}
The main examples of the BBGKY hierarchy are discussed below [a1].
1) For a smooth potential of interaction $\Phi$,
\begin{equation*} ( [ {\cal L , A} ] F ) _ { n } ( X ) = \end{equation*}
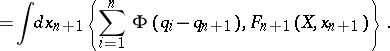 |
2) For a system with singular potential of interaction
\begin{equation*} \Phi ( q ) = \left\{ \begin{array} { l l } { + \infty } & { \text { if } | q | \leq \sigma , } \\ { 0 } & { \text { if } | q | > \sigma , } \end{array} \right. \end{equation*}
like a hard-sphere system of diameter $\sigma$, for dimension $\nu \geq 2$ at $t > 0$ one has
\begin{equation*} ( [ {\cal L , A} ] F ) _ { n } ( X ) = \end{equation*}
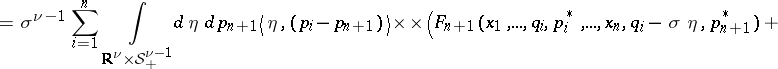 |
\begin{equation*} - F _ { n + 1 } ( X , q _ { i } + \sigma \eta , p _ { n + 1 } ) ), \end{equation*}
where $\langle \, .\, ,\, . \, \rangle$ is the inner product,
\begin{equation*} \mathcal{S} _ { + } ^ { \nu - 1 } = \left\{ \eta \in \mathbf{R} ^ { \nu } : | \eta | = 1 , \langle \eta , ( p _ { i } - p _ { n + 1 } ) \rangle > 0 \right\} \end{equation*}
and
\begin{equation*} p _ { i } ^ { * } = p _ { i } - \eta \langle \eta , ( p _ { i } - p _ { n + 1 } ) \rangle, \end{equation*}
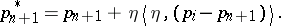 |
3) The dual BBGKY hierarchy
\begin{equation*} \frac { d } { d t } G ( t ) = \mathcal{L} G ( t ) + [ \mathcal{L} , \mathcal{A} ^ { * } ] G ( t ), \end{equation*}
where $\mathcal{A} ^ { * }$ is the adjoint operator to $\mathcal{A}$:
\begin{equation*} ( \mathcal{A} ^ { * } f ) _ { n } ( X ) = \sum _ { i = 1 } ^ { n } f _ { n - 1 } ( x _ { 1 } , \dots , x _ { i - 1} , x _ { i + 1} , \dots , x _ { n } ). \end{equation*}
Such a hierarchy describes the evolution of observables $G ( t )$ of a system of particle.
There are two different approaches to constructing the solutions of the hierarchy: either by iteration or by a functional (cluster expansion) series; see [a1]. The functional representation of the solution for the Cauchy problem depends on symmetry properties of the Hamiltonian and on initial distribution functions
\begin{equation*} F ( 0 ) = ( F _ { 1 } ( 0 , x _ { 1 } ) , \ldots , F _ { n } ( 0 , x _ { 1 } , \ldots , x _ { n } ) , \ldots ). \end{equation*}
In the symmetric case it has the form
\begin{equation*} F _ { s } ( t , x _ { 1 } , \ldots , x _ { s } ) = \end{equation*}
\begin{equation*} = \sum _ { n = 0 } ^ { \infty } \int d x _ { s + 1} \cdots d x _ { s + n} U ^ { ( n )_t } F _ { s + n} ( 0 , x _ { 1 } , \dots , x _ { s + n} ), \end{equation*}
where
\begin{equation*} U ^ { ( n )_ t} = \sum _ { k = 0 } ^ { n } \frac { ( - 1 ) ^ { k } } { k ! ( n - k ) ! } S ^ { s + n - k } ( - t , x _ { 1 } , \dots , x _ { s + n - k} ) \end{equation*}
and the evolution operator $S ^ { n } ( - t , x _ { 1 } , \dots , x _ { n } )$,
\begin{equation*} S ^ { n } ( - t , x _ { 1 } , \dots , x _ { n } ) F _ { n } ( x _ { 1 } , \dots , x _ { n } ) = \end{equation*}
\begin{equation*} = F _ { n } ( X _ { 1 } ( - t , x _ { 1 } , \ldots , x _ { n } ) , \ldots , X _ { n } ( - t , x _ { 1 } , \ldots , x _ { n } ) ), \end{equation*}
shifts the arguments of the functions along the solutions of the Hamilton equations (the phase trajectories) $X _ { i } ( - t , x _ { 1 } , \ldots , x _ { n } )$, $i = 1 , \dots , n$, of a system of $n$ particles with initial data $X _ { i } ( 0 , x _ { i } ) = x _ { i }$. The evolution operators $S ^ { n } ( t )$ form a group of operators generated by the Liouville operator ${\cal L} _ { n }$ defined above. In certain cases this representation of the solution (a cluster expansion) can be treated as the solution $F ( t ) = U ( t ) F ( 0 )$ determined by a group of evolution operators $U ( t )$. In terms of the operators defined above, the group $U ( t )$ has the form
\begin{equation*} U ( t ) = e ^ { \mathcal{A} } S ( - t ) e ^ { - \mathcal{A} }. \end{equation*}
There exist various methods to give a meaning to the formal solution of the Cauchy problem to the BBGKY hierarchy in certain function spaces. For example, the semi-group method (in spaces of sequences of summable functions and, for quantum systems, in the space of sequences of kernel operators), the interaction region method (for constructing an a priori estimate of a solution), the thermodynamic limit method (for the time-continuation of the local solution in the space of sequences of bounded functions), and non-standard analysis methods.
To date (1998), existence and uniqueness results for the BBGKY hierarchy have been proved:
a) in the space $L^1$ of sequences of summable functions (or kernel operators, in the quantum case): time-global solutions for general classes of an interaction potential;
b) in the space $L^{\infty}$ of sequences of functions bounded with respect to the configuration variables and decreasing with respect to the momentum variables: time-global solutions for the BBGKY hierarchy of a hard-sphere system for arbitrary initial data in the one-dimensional case and with initial data close to the equilibrium state in the many-dimensional case; also, time-global solutions for one-dimensional systems of particles interacting by the short-range potential with a hard-core and with initial data close to equilibrium.
The BBGKY hierarchy allows one to describe both equilibrium and non-equilibrium states of many-particle systems from a common point of view. Non-equilibrium states are characterized by the solutions of the initial value problem for this hierarchy and, correspondingly, equilibrium states are characterized by the solutions of the steady BBGKY hierarchy, see [a1], [a3], [a2].
In so-called large-scale limits, asymptotics of solutions to the initial value problem of the BBGKY hierarchy are governed by non-linear kinetic equations (cf. also Kinetic equation) or by hydrodynamic equations depending on initial data. For example, in the Boltzmann–Grad limit the asymptotics of solutions of the BBGKY hierarchy is described by the Boltzmann hierarchy and, as a consequence, for factorized initial data the equation determining the evolution of an initial state is the Boltzmann equation.
General references for this area are [a1], [a4], [a3], [a2], [a5].
References
| [a1] | C. Cercignani, V. Gerasimenko, D. Petrina, "Many-particle dynamics and kinetic equations" , Kluwer Acad. Publ. (1997) |
| [a2] | D. Petrina, V. Gerasimenko, P. Malyshev, "Mathematical foundations of classical statistical mechanics. Continuous systems" , Gordon&Breach (1989) |
| [a3] | D. Petrina, "Mathematical foundations of quantum statistical mechanics" , Kluwer Acad. Publ. (1995) |
| [a4] | C. Cercignani, R. Illner, M. Pulvirenti, "The mathematical theory of dilute gases" , Springer (1994) |
| [a5] | H. Spohn, "Large scale dynamics of interacting particles" , Springer (1991) |
BBGKY hierarchy. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=BBGKY_hierarchy&oldid=16377