Difference between revisions of "Stopping rule"
(Importing text file) |
m (latex details) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 37 formulas, 33 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | Let $I$ denote a fixed (continuous) [[Linear functional|linear functional]] on $C [ a , b ]$. For the numerical approximation of $I$ most often so-called quadrature formulas $Q _ { n }$ are used (cf. also [[Quadrature formula|Quadrature formula]]). These are linear functionals of type | ||
| − | + | \begin{equation} \tag{a1} Q _ { n } [ f ] = \sum _ { v = 1 } ^ { n } a _ { v , n } f ( x _ { v , n } ), \end{equation} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120270/s1202706.png"/></td> </tr></table> |
| − | + | The numbers $a _ { v,n}$ are called the weights of $Q _ { n }$, while the numbers $x _ { v , n }$ are the so-called nodes of $Q _ { n }$. The remainder term of the quadrature formula $Q _ { n }$ is the linear functional $R_n$ defined by | |
| − | + | \begin{equation} \tag{a2} R _ { n } = I - Q _ { n } \end{equation} | |
| − | + | In order to stop a procedure $( Q _ { n_i } [ f ] ) _ { i = 1,2 , \ldots }$, in practice one has to decide whether $R _ { n } [ f ]$ is less than a prescribed tolerance or not. Most of the numerical software packages compute exit criteria using functionals $S _ { m }$ of the same type as $Q _ { n }$, i.e. | |
| − | + | \begin{equation} \tag{a3} S _ { m } [ f ] = \sum _ { v = 1 } ^ { m } b _ { v , m } f ( y_{v , m} ), \end{equation} | |
| − | + | \begin{equation*} \{ x _ { 1 , n} , \dots , x _ { n , n} \} \subseteq \{ y _ { 1 , m} , \dots , y _ { m , m} \}, \end{equation*} | |
| − | + | where $b _ { v , m } \in \bf R$, $y _ { 1 , m} < \ldots < y _ { m , m }$, and where the second condition in (a3) is given with regard to the computational complexity of the procedure (cf. also [[Algorithm, computational complexity of an|Algorithm, computational complexity of an]]). Of course, one "hopes" that for $f$ one has the inequality | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120270/s12027023.png"/></td> <td style="width:5%;text-align:right;" valign="top">(a4)</td></tr></table> |
| − | + | Since the middle of the 1960s, many new and sophisticated algorithms for the numerical approximation of functionals $I$, in particular for numerical integration (cf. [[Integration, numerical|Integration, numerical]]), have been developed. See [[#References|[a2]]], [[#References|[a4]]], [[#References|[a11]]], [[#References|[a13]]] and [[#References|[a3]]], [[#References|[a5]]], [[#References|[a9]]]. Most of these automatic algorithms use one or several estimates for $R_n$ of the type (a4), which often are obtained by the help of a further quadrature formula $Q_l ^ { B }$: | |
| + | |||
| + | \begin{equation} \tag{a5} | R - n [ f ] | \leq \gamma | Q _ { l } ^ { B } [ f ] - Q _ { n } [ f ] |. \end{equation} | ||
| + | |||
| + | Here the values of $\gamma$ are determined by asymptotic properties of $R_n$, respectively $R _ { l } ^ { B }$, as well as by numerical experience (cf. e.g. [[#References|[a1]]], [[#References|[a7]]], [[#References|[a10]]]). For the latter, different testing techniques are used, see e.g. [[#References|[a4]]], [[#References|[a6]]], [[#References|[a12]]], [[#References|[a13]]]. Naturally, a mathematical proof that such estimates (a4), respectively (a5), "almost" hold is not realistic. However, mathematical results describing special classes of functions and special functionals $S _ { m }$, for which such inequalities are valid, may give some hints for practical application. | ||
In particular, let | In particular, let | ||
| − | + | \begin{equation*} A _ { s } ^ { + } = \left\{ \begin{array} { l l } { f : } & { f \in A _ { s } } \\ & { f ^ { ( s ) } \text { has no change of } \operatorname { sign } \operatorname { in } ( a , b ) } \end{array} \right\}. \end{equation*} | |
| − | A functional | + | A functional $S _ { m }$ of type (a3) is called a Peano stopping functional for the quadrature formula $Q _ { n }$ if (a4) holds for every $f \in A _ { s } ^ { + }$. There are several results for this type of stopping functionals which are based on Peano kernel theory; for a survey see [[#References|[a8]]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table> |
| + | <tr><td valign="top">[a1]</td> <td valign="top"> J. Berntsen, T.O. Espelid, "On the use of Gauss quadrature in adaptive automatic integration schemes" ''BIT'' , '''24''' (1989) pp. 239–242</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> H. Brass, "Quadraturverfahren" , Vandenhoeck&Ruprecht (1977)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> "Numerical integration IV" H. Brass (ed.) G. Hämmerlin (ed.) , ''ISNM'' , Birkhäuser (1994)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> P.J. Davis, P. Rabinowitz, "Methods of numerical integration" , Acad. Press (1983) (Edition: Second)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> T.O. Espelid, A. Genz, "Numerical integration - Recent developments, software and applications" , ''NATO ASI C: Math. Physical Sci.'' , '''357''' , Kluwer Acad. Publ. (1992)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> P. Favati, G. Lotti, F. Romani, "Testing automatic quadrature programs" , Calcolo (1992) pp. 169–193</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> K.-J. Förster, "Über Monotonie und Fehlerkontrolle bei den Gregoryschen Quadraturverfahren" ''ZAMM'' , '''67''' (1987) pp. 257–266</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> K.-J. Förster, "A survey of stopping rules in quadrature based on Peano kernel methods" ''Suppl. Rend. Circ. Mat. Palermo II'' , '''33''' (1993) pp. 311–330</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> "Numerical integration - Recent development, software and applications" P. Keast (ed.) G. Fairweather (ed.) , Reidel (1987)</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> D.P. Laurie, "Stratified sequences of nested quadrature formulas" ''Quaest. Math.'' , '''15''' (1992) pp. 365–384</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> J.N. Lyness, "When not to use an automatic quadrature routine" ''SIAM Review'' , '''25''' (1983) pp. 63–87</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> J.N. Lyness, J.J. Kaganove, "A technique for comparing automatic quadrature routines" ''Comput. J.'' , '''20''' (1977) pp. 170–177</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> R. Piessens, E. deDoncker-Kapenga, C.W. Überhuber, D.K. Kahaner, "QUADPACK: a subroutine package for automatic integration" , ''Ser. Comput. Math.'' , '''1''' , Springer (1982)</td></tr> | ||
| + | </table> | ||
Latest revision as of 19:57, 4 February 2024
Let $I$ denote a fixed (continuous) linear functional on $C [ a , b ]$. For the numerical approximation of $I$ most often so-called quadrature formulas $Q _ { n }$ are used (cf. also Quadrature formula). These are linear functionals of type
\begin{equation} \tag{a1} Q _ { n } [ f ] = \sum _ { v = 1 } ^ { n } a _ { v , n } f ( x _ { v , n } ), \end{equation}
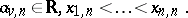 |
The numbers $a _ { v,n}$ are called the weights of $Q _ { n }$, while the numbers $x _ { v , n }$ are the so-called nodes of $Q _ { n }$. The remainder term of the quadrature formula $Q _ { n }$ is the linear functional $R_n$ defined by
\begin{equation} \tag{a2} R _ { n } = I - Q _ { n } \end{equation}
In order to stop a procedure $( Q _ { n_i } [ f ] ) _ { i = 1,2 , \ldots }$, in practice one has to decide whether $R _ { n } [ f ]$ is less than a prescribed tolerance or not. Most of the numerical software packages compute exit criteria using functionals $S _ { m }$ of the same type as $Q _ { n }$, i.e.
\begin{equation} \tag{a3} S _ { m } [ f ] = \sum _ { v = 1 } ^ { m } b _ { v , m } f ( y_{v , m} ), \end{equation}
\begin{equation*} \{ x _ { 1 , n} , \dots , x _ { n , n} \} \subseteq \{ y _ { 1 , m} , \dots , y _ { m , m} \}, \end{equation*}
where $b _ { v , m } \in \bf R$, $y _ { 1 , m} < \ldots < y _ { m , m }$, and where the second condition in (a3) is given with regard to the computational complexity of the procedure (cf. also Algorithm, computational complexity of an). Of course, one "hopes" that for $f$ one has the inequality
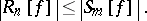 | (a4) |
Since the middle of the 1960s, many new and sophisticated algorithms for the numerical approximation of functionals $I$, in particular for numerical integration (cf. Integration, numerical), have been developed. See [a2], [a4], [a11], [a13] and [a3], [a5], [a9]. Most of these automatic algorithms use one or several estimates for $R_n$ of the type (a4), which often are obtained by the help of a further quadrature formula $Q_l ^ { B }$:
\begin{equation} \tag{a5} | R - n [ f ] | \leq \gamma | Q _ { l } ^ { B } [ f ] - Q _ { n } [ f ] |. \end{equation}
Here the values of $\gamma$ are determined by asymptotic properties of $R_n$, respectively $R _ { l } ^ { B }$, as well as by numerical experience (cf. e.g. [a1], [a7], [a10]). For the latter, different testing techniques are used, see e.g. [a4], [a6], [a12], [a13]. Naturally, a mathematical proof that such estimates (a4), respectively (a5), "almost" hold is not realistic. However, mathematical results describing special classes of functions and special functionals $S _ { m }$, for which such inequalities are valid, may give some hints for practical application.
In particular, let
\begin{equation*} A _ { s } ^ { + } = \left\{ \begin{array} { l l } { f : } & { f \in A _ { s } } \\ & { f ^ { ( s ) } \text { has no change of } \operatorname { sign } \operatorname { in } ( a , b ) } \end{array} \right\}. \end{equation*}
A functional $S _ { m }$ of type (a3) is called a Peano stopping functional for the quadrature formula $Q _ { n }$ if (a4) holds for every $f \in A _ { s } ^ { + }$. There are several results for this type of stopping functionals which are based on Peano kernel theory; for a survey see [a8].
References
| [a1] | J. Berntsen, T.O. Espelid, "On the use of Gauss quadrature in adaptive automatic integration schemes" BIT , 24 (1989) pp. 239–242 |
| [a2] | H. Brass, "Quadraturverfahren" , Vandenhoeck&Ruprecht (1977) |
| [a3] | "Numerical integration IV" H. Brass (ed.) G. Hämmerlin (ed.) , ISNM , Birkhäuser (1994) |
| [a4] | P.J. Davis, P. Rabinowitz, "Methods of numerical integration" , Acad. Press (1983) (Edition: Second) |
| [a5] | T.O. Espelid, A. Genz, "Numerical integration - Recent developments, software and applications" , NATO ASI C: Math. Physical Sci. , 357 , Kluwer Acad. Publ. (1992) |
| [a6] | P. Favati, G. Lotti, F. Romani, "Testing automatic quadrature programs" , Calcolo (1992) pp. 169–193 |
| [a7] | K.-J. Förster, "Über Monotonie und Fehlerkontrolle bei den Gregoryschen Quadraturverfahren" ZAMM , 67 (1987) pp. 257–266 |
| [a8] | K.-J. Förster, "A survey of stopping rules in quadrature based on Peano kernel methods" Suppl. Rend. Circ. Mat. Palermo II , 33 (1993) pp. 311–330 |
| [a9] | "Numerical integration - Recent development, software and applications" P. Keast (ed.) G. Fairweather (ed.) , Reidel (1987) |
| [a10] | D.P. Laurie, "Stratified sequences of nested quadrature formulas" Quaest. Math. , 15 (1992) pp. 365–384 |
| [a11] | J.N. Lyness, "When not to use an automatic quadrature routine" SIAM Review , 25 (1983) pp. 63–87 |
| [a12] | J.N. Lyness, J.J. Kaganove, "A technique for comparing automatic quadrature routines" Comput. J. , 20 (1977) pp. 170–177 |
| [a13] | R. Piessens, E. deDoncker-Kapenga, C.W. Überhuber, D.K. Kahaner, "QUADPACK: a subroutine package for automatic integration" , Ser. Comput. Math. , 1 , Springer (1982) |
Stopping rule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stopping_rule&oldid=15510