|
|
| (3 intermediate revisions by 2 users not shown) |
| Line 1: |
Line 1: |
| | + | <!-- |
| | + | s0867701.png |
| | + | $#A+1 = 97 n = 2 |
| | + | $#C+1 = 97 : ~/encyclopedia/old_files/data/S086/S.0806770 Spinor representation, |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | + | |
| | + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | + | |
| | ''spin representation'' | | ''spin representation'' |
| | | | |
| − | The simplest faithful linear representation (cf. [[Faithful representation|Faithful representation]]; [[Linear representation|Linear representation]]) of the [[Spinor group|spinor group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s0867701.png" />, or the linear representation of the corresponding even Clifford algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s0867702.png" /> (see [[Spinor group|Spinor group]]; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s0867703.png" /> is a [[Quadratic form|quadratic form]]). If the ground field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s0867704.png" /> is algebraically closed, then the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s0867705.png" /> is isomorphic to the complete matrix algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s0867706.png" /> (where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s0867707.png" />) or to the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s0867708.png" /> (where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s0867709.png" />). Therefore there is defined a linear representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677010.png" /> of the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677011.png" /> on the space of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677012.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677013.png" />; this representation is called a spinor representation. The restriction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677014.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677015.png" /> is called the spinor representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677016.png" />. For odd <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677017.png" />, the spinor representation is irreducible, and for even <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677018.png" /> it splits into the direct sum of two non-equivalent irreducible representations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677019.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677020.png" />, which are called half-spin (or) representations. The elements of the space of the spinor representation are called spinors, and those of the space of the half-spinor representation half-spinors. The spinor representation of the spinor group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677021.png" /> is self-dual for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677022.png" />, whereas the half-spinor representations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677024.png" /> of the spinor group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677025.png" /> are self-dual for even <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677026.png" /> and dual to one another for odd <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677027.png" />. The spinor representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677028.png" /> is faithful for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677029.png" />, while the half-spinor representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677030.png" /> are faithful for odd <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677031.png" />, but have a kernel of order two when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677032.png" /> is even. | + | The simplest faithful linear representation (cf. [[Faithful representation|Faithful representation]]; [[Linear representation|Linear representation]]) of the [[Spinor group|spinor group]] $ \mathop{\rm Spin} _ {n} ( Q) $, |
| | + | or the linear representation of the corresponding even Clifford algebra $ C ^ {+} = C ^ {+} ( Q) $( |
| | + | see [[Spinor group|Spinor group]]; $ Q $ |
| | + | is a [[Quadratic form|quadratic form]]). If the ground field $ K $ |
| | + | is algebraically closed, then the algebra $ C ^ {+} $ |
| | + | is isomorphic to the complete matrix algebra $ M _ {2 ^ {m} } ( K) $( |
| | + | where $ n = 2 m + 1 $) |
| | + | or to the algebra $ M _ {2 ^ {m-1} } ( K) \oplus M _ {2 ^ {m-1} } ( K) $( |
| | + | where $ n = 2 m $). |
| | + | Therefore there is defined a linear representation $ \rho $ |
| | + | of the algebra $ C ^ {+} $ |
| | + | on the space of dimension $ 2 ^ {m} $ |
| | + | over $ K $; |
| | + | this representation is called a spinor representation. The restriction of $ \rho $ |
| | + | to $ \mathop{\rm Spin} _ {n} ( Q) $ |
| | + | is called the spinor representation of $ \mathop{\rm Spin} _ {n} ( Q) $. |
| | + | For odd $ n $, |
| | + | the spinor representation is irreducible, and for even $ n $ |
| | + | it splits into the direct sum of two non-equivalent irreducible representations $ \rho ^ \prime $ |
| | + | and $ \rho ^ {\prime\prime} $, |
| | + | which are called half-spin (or) representations. The elements of the space of the spinor representation are called spinors, and those of the space of the half-spinor representation half-spinors. The spinor representation of the spinor group $ \mathop{\rm Spin} _ {n} $ |
| | + | is self-dual for any $ n \geq 3 $, |
| | + | whereas the half-spinor representations $ \rho ^ \prime $ |
| | + | and $ \rho ^ {\prime\prime} $ |
| | + | of the spinor group $ \mathop{\rm Spin} _ {2m} $ |
| | + | are self-dual for even $ m $ |
| | + | and dual to one another for odd $ m $. |
| | + | The spinor representation of $ \mathop{\rm Spin} _ {n} $ |
| | + | is faithful for all $ n \geq 3 $, |
| | + | while the half-spinor representations of $ \mathop{\rm Spin} _ {2m} $ |
| | + | are faithful for odd $ m $, |
| | + | but have a kernel of order two when $ m $ |
| | + | is even. |
| | | | |
| − | For a quadratic form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677033.png" /> on a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677034.png" /> over some subfield <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677035.png" />, the spinor representation is not always defined over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677036.png" />. However, if the Witt index of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677037.png" /> is maximal, that is, equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677038.png" /> (in particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677039.png" /> is algebraically closed), then the spinor and half-spinor representations are defined over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677040.png" />. In this case these representations can be described in the following way if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677041.png" /> (see [[#References|[1]]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677042.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677043.png" /> be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677044.png" />-subspaces of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677045.png" />-space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677046.png" /> that are maximal totally isotropic (with respect to the symmetric bilinear form on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677047.png" /> associated with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677048.png" />) and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677049.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677050.png" /> be the subalgebra of the Clifford algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677051.png" /> generated by the subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677052.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677053.png" /> be the product of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677054.png" /> vectors forming a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677055.png" />-basis of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677056.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677057.png" /> is even, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677058.png" />, then the spinor representation is realized in the left ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677059.png" /> and acts there by left translation: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677060.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677061.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677062.png" />). Furthermore, the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677063.png" /> defines an isomorphism of vector spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677064.png" /> that enables one to realize the spinor representation in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677065.png" />, which is naturally isomorphic to the exterior algebra over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677066.png" />. The half-spinor representations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677067.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677068.png" /> are realized in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677069.png" />-dimensional subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677070.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677071.png" />. | + | For a quadratic form $ Q $ |
| | + | on a space $ V $ |
| | + | over some subfield $ k \subset K $, |
| | + | the spinor representation is not always defined over $ k $. |
| | + | However, if the Witt index of $ Q $ |
| | + | is maximal, that is, equal to $ [ n / 2 ] $( |
| | + | in particular, if $ k $ |
| | + | is algebraically closed), then the spinor and half-spinor representations are defined over $ k $. |
| | + | In this case these representations can be described in the following way if $ \mathop{\rm char} k \neq 2 $( |
| | + | see [[#References|[1]]]). Let $ L $ |
| | + | and $ M $ |
| | + | be $ k $- |
| | + | subspaces of the $ k $- |
| | + | space $ V $ |
| | + | that are maximal totally isotropic (with respect to the symmetric bilinear form on $ V $ |
| | + | associated with $ Q $) |
| | + | and let $ L \cap M = 0 $. |
| | + | Let $ C _ {L} $ |
| | + | be the subalgebra of the Clifford algebra $ C = C ( Q) $ |
| | + | generated by the subspace $ L \subset V $, |
| | + | and let $ e _ {M} \in C $ |
| | + | be the product of $ m $ |
| | + | vectors forming a $ k $- |
| | + | basis of $ M $. |
| | + | If $ n $ |
| | + | is even, $ n = 2m $, |
| | + | then the spinor representation is realized in the left ideal $ C e _ {M} $ |
| | + | and acts there by left translation: $ \rho ( s) x = s x $( |
| | + | $ s \in C ^ {+} $, |
| | + | $ x \in C e _ {M} $). |
| | + | Furthermore, the mapping $ x \mapsto x e _ {M} $ |
| | + | defines an isomorphism of vector spaces $ C _ {L} \rightarrow C e _ {M} $ |
| | + | that enables one to realize the spinor representation in $ C _ {L} $, |
| | + | which is naturally isomorphic to the exterior algebra over $ L $. |
| | + | The half-spinor representations $ \rho ^ \prime $ |
| | + | and $ \rho ^ {\prime\prime} $ |
| | + | are realized in the $ 2 ^ {m-1} $- |
| | + | dimensional subspaces $ C _ {L} \cap C ^ {+} $ |
| | + | and $ C _ {L} \cap C ^ {-} $. |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677072.png" /> is odd, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677073.png" /> can be imbedded in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677074.png" />-dimensional vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677075.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677076.png" />. One defines a quadratic form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677077.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677078.png" /> by putting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677079.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677080.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677081.png" />. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677082.png" /> is a non-degenerate quadratic form of maximal Witt index defined over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677083.png" /> on the even-dimensional vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677084.png" />. The spinor representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677085.png" /> (or of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677086.png" />) is obtained by restricting any of the half-spinor representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677087.png" /> (or of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677088.png" />) to the subalgebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677089.png" /> (or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677090.png" />, respectively). | + | If $ n $ |
| | + | is odd, then $ V $ |
| | + | can be imbedded in the $ ( n + 1 ) $- |
| | + | dimensional vector space $ V _ {1} = V \oplus k \epsilon $ |
| | + | over $ k $. |
| | + | One defines a quadratic form $ Q _ {1} $ |
| | + | on $ V _ {1} $ |
| | + | by putting $ Q _ {1} ( v + \epsilon ) = Q ( v) - \lambda ^ {2} $ |
| | + | for all $ v \in V $ |
| | + | and $ \lambda \in k $. |
| | + | $ Q _ {1} $ |
| | + | is a non-degenerate quadratic form of maximal Witt index defined over $ k $ |
| | + | on the even-dimensional vector space $ V _ {1} $. |
| | + | The spinor representation of $ C ^ {+} ( Q) $( |
| | + | or of $ \mathop{\rm Spin} _ {n} ( Q) $) |
| | + | is obtained by restricting any of the half-spinor representations of $ C ^ {+} ( Q _ {1} ) $( |
| | + | or of $ \mathop{\rm Spin} _ {n+} 1 ( Q _ {1} ) $) |
| | + | to the subalgebra $ C ^ {+} ( Q) $( |
| | + | or $ \mathop{\rm Spin} _ {n} ( Q) $, |
| | + | respectively). |
| | | | |
| − | The problem of classifying spinors has been solved when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677091.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677092.png" /> is an algebraically closed field of characteristic 0 (see [[#References|[4]]], [[#References|[8]]], [[#References|[9]]]). The problem consists of the following: 1) describe the orbits of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677093.png" /> in the spinor space by giving a representative of each orbit; 2) calculate the stabilizers in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677094.png" /> of each of these representatives; and 3) describe the algebra of invariants of the linear group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677095.png" />. | + | The problem of classifying spinors has been solved when $ 3 \leq n \leq 14 $ |
| | + | and $ k $ |
| | + | is an algebraically closed field of characteristic 0 (see [[#References|[4]]], [[#References|[8]]], [[#References|[9]]]). The problem consists of the following: 1) describe the orbits of $ \rho ( \mathop{\rm Spin} _ {n} ) $ |
| | + | in the spinor space by giving a representative of each orbit; 2) calculate the stabilizers in $ \mathop{\rm Spin} _ {n} $ |
| | + | of each of these representatives; and 3) describe the algebra of invariants of the linear group $ \rho ( \mathop{\rm Spin} _ {n} ) $. |
| | | | |
| − | The existence of spinor and half-spinor representations of the Lie algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677096.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677097.png" /> was discovered by E. Cartan in 1913, when he classified the finite-dimensional representations of simple Lie algebras [[#References|[6]]]. In 1935, R. Brauer and H. Weyl described spinor and half-spinor representations in terms of Clifford algebras [[#References|[5]]]. P. Dirac [[#References|[3]]] showed how spinors could be used in quantum mechanics to describe the rotation of an electron. | + | The existence of spinor and half-spinor representations of the Lie algebra $ \mathfrak s \mathfrak p _ {n} $ |
| | + | of $ \mathop{\rm Spin} _ {n} $ |
| | + | was discovered by E. Cartan in 1913, when he classified the finite-dimensional representations of simple Lie algebras [[#References|[6]]]. In 1935, R. Brauer and H. Weyl described spinor and half-spinor representations in terms of Clifford algebras [[#References|[5]]]. P. Dirac [[#References|[3]]] showed how spinors could be used in quantum mechanics to describe the rotation of an electron. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Algèbre" , ''Eléments de mathématiques'' , Hermann (1970) pp. Chapt. II. Algèbre linéaire</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Weyl, "Classical groups, their invariants and representations" , Princeton Univ. Press (1946) (Translated from German)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.A.M. Dirac, "Principles of quantum mechanics" , Clarendon Press (1958)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.L. Popov, "Classification of spinors of dimension fourteen" ''Trans. Moscow Math. Soc.'' , '''1''' (1980) pp. 181–232 ''Trudy Moskov. Mat. Obshch.'' , '''37''' (1978) pp. 173–217</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> R. Brauer, H. Weyl, "Spinors in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677098.png" />-dimensions" ''Amer. J. Math.'' , '''57''' : 2 (1935) pp. 425–449</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E. Cartan, "Les groupes projectifs qui ne laissant invariante aucune multiplicité plane" ''Bull. Soc. Math. France'' , '''41''' (1913) pp. 53–96</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> C. Chevalley, "The algebraic theory of spinors" , Columbia Univ. Press (1954)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> V. Gatti, E. Viniberghi, "Spinors in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677099.png" />-dimensional space" ''Adv. Math.'' , '''30''' : 2 (1978) pp. 137–155</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> J.I. Igusa, "A classification of spinors up to dimension twelve" ''Amer. J. Math.'' , '''92''' : 4 (1970) pp. 997–1028</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Algèbre" , ''Eléments de mathématiques'' , Hermann (1970) pp. Chapt. II. Algèbre linéaire {{MR|0274237}} {{ZBL|0211.02401}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Weyl, "Classical groups, their invariants and representations" , Princeton Univ. Press (1946) (Translated from German) {{MR|0000255}} {{ZBL|1024.20502}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.A.M. Dirac, "Principles of quantum mechanics" , Clarendon Press (1958) {{MR|2303789}} {{MR|0116921}} {{MR|0023198}} {{MR|1522388}} {{ZBL|0080.22005}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.L. Popov, "Classification of spinors of dimension fourteen" ''Trans. Moscow Math. Soc.'' , '''1''' (1980) pp. 181–232 ''Trudy Moskov. Mat. Obshch.'' , '''37''' (1978) pp. 173–217 {{MR|0514331}} {{ZBL|0443.20038}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> R. Brauer, H. Weyl, "Spinors in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677098.png" />-dimensions" ''Amer. J. Math.'' , '''57''' : 2 (1935) pp. 425–449 {{MR|1507084}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E. Cartan, "Les groupes projectifs qui ne laissant invariante aucune multiplicité plane" ''Bull. Soc. Math. France'' , '''41''' (1913) pp. 53–96</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> C. Chevalley, "The algebraic theory of spinors" , Columbia Univ. Press (1954) {{MR|0060497}} {{ZBL|0057.25901}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> V. Gatti, E. Viniberghi, "Spinors in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086770/s08677099.png" />-dimensional space" ''Adv. Math.'' , '''30''' : 2 (1978) pp. 137–155</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> J.I. Igusa, "A classification of spinors up to dimension twelve" ''Amer. J. Math.'' , '''92''' : 4 (1970) pp. 997–1028 {{MR|0277558}} {{ZBL|0217.36203}} </TD></TR></table> |
spin representation
The simplest faithful linear representation (cf. Faithful representation; Linear representation) of the spinor group $ \mathop{\rm Spin} _ {n} ( Q) $,
or the linear representation of the corresponding even Clifford algebra $ C ^ {+} = C ^ {+} ( Q) $(
see Spinor group; $ Q $
is a quadratic form). If the ground field $ K $
is algebraically closed, then the algebra $ C ^ {+} $
is isomorphic to the complete matrix algebra $ M _ {2 ^ {m} } ( K) $(
where $ n = 2 m + 1 $)
or to the algebra $ M _ {2 ^ {m-1} } ( K) \oplus M _ {2 ^ {m-1} } ( K) $(
where $ n = 2 m $).
Therefore there is defined a linear representation $ \rho $
of the algebra $ C ^ {+} $
on the space of dimension $ 2 ^ {m} $
over $ K $;
this representation is called a spinor representation. The restriction of $ \rho $
to $ \mathop{\rm Spin} _ {n} ( Q) $
is called the spinor representation of $ \mathop{\rm Spin} _ {n} ( Q) $.
For odd $ n $,
the spinor representation is irreducible, and for even $ n $
it splits into the direct sum of two non-equivalent irreducible representations $ \rho ^ \prime $
and $ \rho ^ {\prime\prime} $,
which are called half-spin (or) representations. The elements of the space of the spinor representation are called spinors, and those of the space of the half-spinor representation half-spinors. The spinor representation of the spinor group $ \mathop{\rm Spin} _ {n} $
is self-dual for any $ n \geq 3 $,
whereas the half-spinor representations $ \rho ^ \prime $
and $ \rho ^ {\prime\prime} $
of the spinor group $ \mathop{\rm Spin} _ {2m} $
are self-dual for even $ m $
and dual to one another for odd $ m $.
The spinor representation of $ \mathop{\rm Spin} _ {n} $
is faithful for all $ n \geq 3 $,
while the half-spinor representations of $ \mathop{\rm Spin} _ {2m} $
are faithful for odd $ m $,
but have a kernel of order two when $ m $
is even.
For a quadratic form $ Q $
on a space $ V $
over some subfield $ k \subset K $,
the spinor representation is not always defined over $ k $.
However, if the Witt index of $ Q $
is maximal, that is, equal to $ [ n / 2 ] $(
in particular, if $ k $
is algebraically closed), then the spinor and half-spinor representations are defined over $ k $.
In this case these representations can be described in the following way if $ \mathop{\rm char} k \neq 2 $(
see [1]). Let $ L $
and $ M $
be $ k $-
subspaces of the $ k $-
space $ V $
that are maximal totally isotropic (with respect to the symmetric bilinear form on $ V $
associated with $ Q $)
and let $ L \cap M = 0 $.
Let $ C _ {L} $
be the subalgebra of the Clifford algebra $ C = C ( Q) $
generated by the subspace $ L \subset V $,
and let $ e _ {M} \in C $
be the product of $ m $
vectors forming a $ k $-
basis of $ M $.
If $ n $
is even, $ n = 2m $,
then the spinor representation is realized in the left ideal $ C e _ {M} $
and acts there by left translation: $ \rho ( s) x = s x $(
$ s \in C ^ {+} $,
$ x \in C e _ {M} $).
Furthermore, the mapping $ x \mapsto x e _ {M} $
defines an isomorphism of vector spaces $ C _ {L} \rightarrow C e _ {M} $
that enables one to realize the spinor representation in $ C _ {L} $,
which is naturally isomorphic to the exterior algebra over $ L $.
The half-spinor representations $ \rho ^ \prime $
and $ \rho ^ {\prime\prime} $
are realized in the $ 2 ^ {m-1} $-
dimensional subspaces $ C _ {L} \cap C ^ {+} $
and $ C _ {L} \cap C ^ {-} $.
If $ n $
is odd, then $ V $
can be imbedded in the $ ( n + 1 ) $-
dimensional vector space $ V _ {1} = V \oplus k \epsilon $
over $ k $.
One defines a quadratic form $ Q _ {1} $
on $ V _ {1} $
by putting $ Q _ {1} ( v + \epsilon ) = Q ( v) - \lambda ^ {2} $
for all $ v \in V $
and $ \lambda \in k $.
$ Q _ {1} $
is a non-degenerate quadratic form of maximal Witt index defined over $ k $
on the even-dimensional vector space $ V _ {1} $.
The spinor representation of $ C ^ {+} ( Q) $(
or of $ \mathop{\rm Spin} _ {n} ( Q) $)
is obtained by restricting any of the half-spinor representations of $ C ^ {+} ( Q _ {1} ) $(
or of $ \mathop{\rm Spin} _ {n+} 1 ( Q _ {1} ) $)
to the subalgebra $ C ^ {+} ( Q) $(
or $ \mathop{\rm Spin} _ {n} ( Q) $,
respectively).
The problem of classifying spinors has been solved when $ 3 \leq n \leq 14 $
and $ k $
is an algebraically closed field of characteristic 0 (see [4], [8], [9]). The problem consists of the following: 1) describe the orbits of $ \rho ( \mathop{\rm Spin} _ {n} ) $
in the spinor space by giving a representative of each orbit; 2) calculate the stabilizers in $ \mathop{\rm Spin} _ {n} $
of each of these representatives; and 3) describe the algebra of invariants of the linear group $ \rho ( \mathop{\rm Spin} _ {n} ) $.
The existence of spinor and half-spinor representations of the Lie algebra $ \mathfrak s \mathfrak p _ {n} $
of $ \mathop{\rm Spin} _ {n} $
was discovered by E. Cartan in 1913, when he classified the finite-dimensional representations of simple Lie algebras [6]. In 1935, R. Brauer and H. Weyl described spinor and half-spinor representations in terms of Clifford algebras [5]. P. Dirac [3] showed how spinors could be used in quantum mechanics to describe the rotation of an electron.
References
| [1] | N. Bourbaki, "Algèbre" , Eléments de mathématiques , Hermann (1970) pp. Chapt. II. Algèbre linéaire MR0274237 Zbl 0211.02401 |
| [2] | H. Weyl, "Classical groups, their invariants and representations" , Princeton Univ. Press (1946) (Translated from German) MR0000255 Zbl 1024.20502 |
| [3] | P.A.M. Dirac, "Principles of quantum mechanics" , Clarendon Press (1958) MR2303789 MR0116921 MR0023198 MR1522388 Zbl 0080.22005 |
| [4] | V.L. Popov, "Classification of spinors of dimension fourteen" Trans. Moscow Math. Soc. , 1 (1980) pp. 181–232 Trudy Moskov. Mat. Obshch. , 37 (1978) pp. 173–217 MR0514331 Zbl 0443.20038 |
| [5] | R. Brauer, H. Weyl, "Spinors in  -dimensions" Amer. J. Math. , 57 : 2 (1935) pp. 425–449 MR1507084 -dimensions" Amer. J. Math. , 57 : 2 (1935) pp. 425–449 MR1507084 |
| [6] | E. Cartan, "Les groupes projectifs qui ne laissant invariante aucune multiplicité plane" Bull. Soc. Math. France , 41 (1913) pp. 53–96 |
| [7] | C. Chevalley, "The algebraic theory of spinors" , Columbia Univ. Press (1954) MR0060497 Zbl 0057.25901 |
| [8] | V. Gatti, E. Viniberghi, "Spinors in 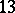 -dimensional space" Adv. Math. , 30 : 2 (1978) pp. 137–155 -dimensional space" Adv. Math. , 30 : 2 (1978) pp. 137–155 |
| [9] | J.I. Igusa, "A classification of spinors up to dimension twelve" Amer. J. Math. , 92 : 4 (1970) pp. 997–1028 MR0277558 Zbl 0217.36203 |
 -dimensions" Amer. J. Math. , 57 : 2 (1935) pp. 425–449 MR1507084
-dimensions" Amer. J. Math. , 57 : 2 (1935) pp. 425–449 MR1507084 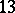 -dimensional space" Adv. Math. , 30 : 2 (1978) pp. 137–155
-dimensional space" Adv. Math. , 30 : 2 (1978) pp. 137–155