Difference between revisions of "Rational tangles"
(Importing text file) |
|||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 12 formulas, 10 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|done}} | |
| − | <img | + | A family of $2$-tangles (cf. [[Tangle]]) classified by J.H. Conway. The $2$-tangle of Fig. a1 is called a rational tangle with Conway notation $T ( a _ { 1 } , \dots , a _ { n } )$. It is a rational $p / q$-tangle if |
| + | |||
| + | \begin{equation*} \frac { p } { q } = a _ { n } + \frac { 1 } { a _ { n - 1} + \ldots + \frac { 1 } { a_ { 1 } } }. \end{equation*} | ||
| + | |||
| + | The fraction $p / q$ is called the slope of the tangle and can be identified with the slope of the meridian disc of the solid torus that is the branched double covering of the rational tangle. | ||
| + | |||
| + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/r130030a.gif" style="border:1px solid;"/> | ||
Figure: r130030a | Figure: r130030a | ||
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/r130030b.gif" style="border:1px solid;"/> |
Figure: r130030b | Figure: r130030b | ||
| − | Conway proved that two rational tangles are ambient isotopic (with boundary fixed) if and only if their slopes are equal. A rational | + | Conway proved that two rational tangles are ambient isotopic (with boundary fixed) if and only if their slopes are equal. A rational $n$-tangle (also called an $n$-bridge $n$-tangle) is an $n$-tangle that can be obtained from the identity tangle by a finite number of additions of a single crossing. |
====References==== | ====References==== | ||
| − | + | ||
| + | * {{Ref|a1}} J.H. Conway, "An enumeration of knots and links" J. Leech (ed.), ''Computational Problems in Abstract Algebra'', Pergamon Press (1969) pp. 329–358 {{ZBL|0202.54703}} | ||
| + | * {{Ref|a2}} A. Kawauchi, "A survey of knot theory", Birkhäuser (1996) {{ZBL|0861.57001}} | ||
| + | |||
| + | {{OldImage}} | ||
Latest revision as of 07:50, 25 November 2023
A family of $2$-tangles (cf. Tangle) classified by J.H. Conway. The $2$-tangle of Fig. a1 is called a rational tangle with Conway notation $T ( a _ { 1 } , \dots , a _ { n } )$. It is a rational $p / q$-tangle if
\begin{equation*} \frac { p } { q } = a _ { n } + \frac { 1 } { a _ { n - 1} + \ldots + \frac { 1 } { a_ { 1 } } }. \end{equation*}
The fraction $p / q$ is called the slope of the tangle and can be identified with the slope of the meridian disc of the solid torus that is the branched double covering of the rational tangle.

Figure: r130030a
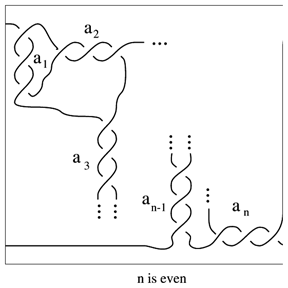
Figure: r130030b
Conway proved that two rational tangles are ambient isotopic (with boundary fixed) if and only if their slopes are equal. A rational $n$-tangle (also called an $n$-bridge $n$-tangle) is an $n$-tangle that can be obtained from the identity tangle by a finite number of additions of a single crossing.
References
- [a1] J.H. Conway, "An enumeration of knots and links" J. Leech (ed.), Computational Problems in Abstract Algebra, Pergamon Press (1969) pp. 329–358 Zbl 0202.54703
- [a2] A. Kawauchi, "A survey of knot theory", Birkhäuser (1996) Zbl 0861.57001
Rational tangles. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_tangles&oldid=13459