Difference between revisions of "Néron-Severi group"
Ulf Rehmann (talk | contribs) m (moved Néron–Severi group to Neron-Severi group: ascii title) |
|||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
The divisor class group under algebraic equivalence on a non-singular projective variety. | The divisor class group under algebraic equivalence on a non-singular projective variety. | ||
| − | Let | + | Let $X$ be a non-singular projective variety of dimension $\ge 2$ defined over an [[algebraically closed field]] $k$, let $D(X)$ be the group of divisors of $X$ and let $D_{\mathrm{a}}(X)$ be the subgroup of divisors that are algebraically equivalent to zero. The quotient group $D(X)/D_{\mathrm{a}}(X)$ is called the Néron–Severi group of $X$ and is denoted by $\mathrm{NS}(X)$. The Néron–Severi theorem asserts that the Abelian group $\mathrm{NS}(X)$ is finitely generated. |
| − | In the case | + | In the case $k = \mathbf{C}$, F. Severi presented, in a series of papers on the theory of the base (see, for example, [[#References|[1]]]), a proof of this theorem using topological and transcendental tools. The first abstract proof (valid for a field of arbitrary characteristic) is due to A. Néron (see [[#References|[2]]], [[#References|[3]]], and also [[#References|[4]]]). |
| − | The rank of | + | The rank of $\mathrm{NS}(X)$ is the algebraic [[Betti number|Betti number]] of the group of divisors on $X$, that is, the algebraic rank of $X$. This is also called the ''Picard number'' of the variety $X$. The elements of the finite torsion subgroup $\mathrm{NS}_{\mathrm{tors}}(X)$ are called ''Severi divisors'', and the order of this subgroup is called the ''Severi number''; the group $\mathrm{NS}_{\mathrm{tors}}(X)$ is a birational invariant (see [[#References|[6]]]). |
There are generalizations of the Néron–Severi theorem to other groups of classes of algebraic cycles (see [[#References|[1]]] (classical theory) and [[#References|[7]]] (modern theory)). | There are generalizations of the Néron–Severi theorem to other groups of classes of algebraic cycles (see [[#References|[1]]] (classical theory) and [[#References|[7]]] (modern theory)). | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> F. Severi, "La base per le varietà algebriche di dimensione qualunque contenute in una data e la teoria generale delle corrispondénze fra i punti di due superficie algebriche" ''Mem. Accad. Ital.'' , '''5''' (1934) pp. 239–283</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Néron, "Problèmes arithmétiques et géometriques attachée à la notion de rang d'une courbe algébrique dans un corps" ''Bull. Soc. Math. France'' , '''80''' (1952) pp. 101–166</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Néron, "La théorie de la base pour les diviseurs sur les variétés algébriques" , ''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066300/n06630018.png" /> Coll. Géom. Alg. Liège'' , G. Thone (1952) pp. 119–126</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S. Lang, A. Néron, "Rational points of abelian varieties over function fields" ''Amer. J. Math.'' , '''81''' (1959) pp. 95–118</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M. Baldassarri, "Algebraic varieties" , Springer (1956)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> I.V. Dolgachev, V.A. Iskovskikh, "Geometry of algebraic varieties" ''J. Soviet Math.'' , '''5''' : 6 (1976) pp. 803–864 ''Itogi Nauk. i Tekhn. Algebra. Topol. Geom.'' , '''12''' (1974) pp. 77–170</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> F. Severi, "La base per le varietà algebriche di dimensione qualunque contenute in una data e la teoria generale delle corrispondénze fra i punti di due superficie algebriche" ''Mem. Accad. Ital.'' , '''5''' (1934) pp. 239–283</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> A. Néron, "Problèmes arithmétiques et géometriques attachée à la notion de rang d'une courbe algébrique dans un corps" ''Bull. Soc. Math. France'' , '''80''' (1952) pp. 101–166</TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> A. Néron, "La théorie de la base pour les diviseurs sur les variétés algébriques" , ''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066300/n06630018.png" /> Coll. Géom. Alg. Liège'' , G. Thone (1952) pp. 119–126</TD></TR> | ||
| + | <TR><TD valign="top">[4]</TD> <TD valign="top"> S. Lang, A. Néron, "Rational points of abelian varieties over function fields" ''Amer. J. Math.'' , '''81''' (1959) pp. 95–118</TD></TR> | ||
| + | <TR><TD valign="top">[5]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977)</TD></TR> | ||
| + | <TR><TD valign="top">[6]</TD> <TD valign="top"> M. Baldassarri, "Algebraic varieties" , Springer (1956)</TD></TR> | ||
| + | <TR><TD valign="top">[7]</TD> <TD valign="top"> I.V. Dolgachev, V.A. Iskovskikh, "Geometry of algebraic varieties" ''J. Soviet Math.'' , '''5''' : 6 (1976) pp. 803–864 ''Itogi Nauk. i Tekhn. Algebra. Topol. Geom.'' , '''12''' (1974) pp. 77–170</TD></TR> | ||
| + | </table> | ||
| Line 17: | Line 25: | ||
A study of the Picard number of a certain number of algebraic varieties has been made by T. Shioda. | A study of the Picard number of a certain number of algebraic varieties has been made by T. Shioda. | ||
| − | The phrase "theory | + | The phrase "theory of the base" is a somewhat old-fashioned one and refers to the considerations involved in proving that $\mathrm{NS}(X)$ is a finitely-generated Abelian group and indicating an explicit minimal set of generators (a minimal base in the terminology of Severi), cf. e.g. [[#References|[a4]]], Sect. V.7 (for the case of surfaces). |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T. Shioda, "On the Picard number of a complex projective variety" ''Ann. Sci. Ecole Norm. Sup.'' , '''14''' (1981) pp. 303–321</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> T. Shioda, "On the Picard number of a Fermat surface" ''J. Fac. Sci. Univ. Tokyo'' , '''28''' (1982) pp. 724–734</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> T. Shioda, "An explicit algorithm for computing the Picard number of certain algebraic surfaces" ''Amer. J. Math.'' , '''108''' (1986) pp. 415–432</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> O. Zariski, "Algebraic surfaces" , Springer (1935)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> T. Shioda, "On the Picard number of a complex projective variety" ''Ann. Sci. Ecole Norm. Sup.'' , '''14''' (1981) pp. 303–321</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> T. Shioda, "On the Picard number of a Fermat surface" ''J. Fac. Sci. Univ. Tokyo'' , '''28''' (1982) pp. 724–734</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> T. Shioda, "An explicit algorithm for computing the Picard number of certain algebraic surfaces" ''Amer. J. Math.'' , '''108''' (1986) pp. 415–432</TD></TR> | ||
| + | <TR><TD valign="top">[a4]</TD> <TD valign="top"> O. Zariski, "Algebraic surfaces" , Springer (1935)</TD></TR> | ||
| + | </table> | ||
| + | |||
| + | {{TEX|done}} | ||
Latest revision as of 05:47, 15 April 2023
The divisor class group under algebraic equivalence on a non-singular projective variety.
Let $X$ be a non-singular projective variety of dimension $\ge 2$ defined over an algebraically closed field $k$, let $D(X)$ be the group of divisors of $X$ and let $D_{\mathrm{a}}(X)$ be the subgroup of divisors that are algebraically equivalent to zero. The quotient group $D(X)/D_{\mathrm{a}}(X)$ is called the Néron–Severi group of $X$ and is denoted by $\mathrm{NS}(X)$. The Néron–Severi theorem asserts that the Abelian group $\mathrm{NS}(X)$ is finitely generated.
In the case $k = \mathbf{C}$, F. Severi presented, in a series of papers on the theory of the base (see, for example, [1]), a proof of this theorem using topological and transcendental tools. The first abstract proof (valid for a field of arbitrary characteristic) is due to A. Néron (see [2], [3], and also [4]).
The rank of $\mathrm{NS}(X)$ is the algebraic Betti number of the group of divisors on $X$, that is, the algebraic rank of $X$. This is also called the Picard number of the variety $X$. The elements of the finite torsion subgroup $\mathrm{NS}_{\mathrm{tors}}(X)$ are called Severi divisors, and the order of this subgroup is called the Severi number; the group $\mathrm{NS}_{\mathrm{tors}}(X)$ is a birational invariant (see [6]).
There are generalizations of the Néron–Severi theorem to other groups of classes of algebraic cycles (see [1] (classical theory) and [7] (modern theory)).
References
| [1] | F. Severi, "La base per le varietà algebriche di dimensione qualunque contenute in una data e la teoria generale delle corrispondénze fra i punti di due superficie algebriche" Mem. Accad. Ital. , 5 (1934) pp. 239–283 |
| [2] | A. Néron, "Problèmes arithmétiques et géometriques attachée à la notion de rang d'une courbe algébrique dans un corps" Bull. Soc. Math. France , 80 (1952) pp. 101–166 |
| [3] | A. Néron, "La théorie de la base pour les diviseurs sur les variétés algébriques" , 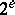 Coll. Géom. Alg. Liège , G. Thone (1952) pp. 119–126 Coll. Géom. Alg. Liège , G. Thone (1952) pp. 119–126 |
| [4] | S. Lang, A. Néron, "Rational points of abelian varieties over function fields" Amer. J. Math. , 81 (1959) pp. 95–118 |
| [5] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [6] | M. Baldassarri, "Algebraic varieties" , Springer (1956) |
| [7] | I.V. Dolgachev, V.A. Iskovskikh, "Geometry of algebraic varieties" J. Soviet Math. , 5 : 6 (1976) pp. 803–864 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 12 (1974) pp. 77–170 |
Comments
A study of the Picard number of a certain number of algebraic varieties has been made by T. Shioda.
The phrase "theory of the base" is a somewhat old-fashioned one and refers to the considerations involved in proving that $\mathrm{NS}(X)$ is a finitely-generated Abelian group and indicating an explicit minimal set of generators (a minimal base in the terminology of Severi), cf. e.g. [a4], Sect. V.7 (for the case of surfaces).
References
| [a1] | T. Shioda, "On the Picard number of a complex projective variety" Ann. Sci. Ecole Norm. Sup. , 14 (1981) pp. 303–321 |
| [a2] | T. Shioda, "On the Picard number of a Fermat surface" J. Fac. Sci. Univ. Tokyo , 28 (1982) pp. 724–734 |
| [a3] | T. Shioda, "An explicit algorithm for computing the Picard number of certain algebraic surfaces" Amer. J. Math. , 108 (1986) pp. 415–432 |
| [a4] | O. Zariski, "Algebraic surfaces" , Springer (1935) |
Néron-Severi group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=N%C3%A9ron-Severi_group&oldid=22835