Difference between revisions of "D'Alembert equation for finite sum decompositions"
m (AUTOMATIC EDIT (latexlist): Replaced 9 formulas out of 11 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (→References: + ZBL link) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 11 formulas, 9 were replaced by TEX code.--> | Out of 11 formulas, 9 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
Consider the decomposition of a function $h ( x , y )$ into a finite sum of the form | Consider the decomposition of a function $h ( x , y )$ into a finite sum of the form | ||
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><tr><td valign="top">[a1]</td> <td valign="top"> M. Čadek, J. Šimša, "Decomposable functions of several variables" ''Aequat. Math.'' , '''40''' (1990) pp. 8–25</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> H. Gauchman, L.A. Rubel, "Sums of products of functions of $x$ times functions of $y$" ''Linear Alg. & Its Appl.'' , '''125''' (1989) pp. 19–63</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> F. Neuman, "Factorizations of matrices and functions of two variables" ''Czech. Math. J.'' , '''32''' : 107 (1982) pp. 582–588</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> F. Neuman, "Functions of two variables and matrices involving factorizations" ''C.R. Math. Rept. Acad. Sci. Canada'' , '''3''' (1981) pp. 7–11</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> F. Neuman, Th. Rassias, "Functions decomposable into finite sums of products" , ''Constantin Catathéodory–An Internat. Tribute'' , '''II''' , World Sci. (1991) pp. 956–963</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> C.M. Stéphanos, "Sur une categorie d'équations fonctionalles" , ''Math. Kongr. Heidelberg'' , '''1905''' (1904) pp. 200–201</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> C.M. Stéphanos, "Sur une categorie d'équations fonctionalles" ''Rend. Circ. Mat. Palermo'' , '''18''' (1904) pp. 360–362</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> Th.M. Rassias, J. Šimša, "Finite sum decompositions in mathematical analysis" , Wiley (1995)</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> Th.M. Rassias, J. Šimša, "19 Remark" ''Aequat. Math.'' , '''56''' (1998) pp. 310</td></tr></table> | + | <table> |
| + | <tr><td valign="top">[a1]</td> <td valign="top"> M. Čadek, J. Šimša, "Decomposable functions of several variables" ''Aequat. Math.'' , '''40''' (1990) pp. 8–25</td></tr> | ||
| + | <tr><td valign="top">[a2]</td> <td valign="top"> H. Gauchman, L.A. Rubel, "Sums of products of functions of $x$ times functions of $y$" ''Linear Alg. & Its Appl.'' , '''125''' (1989) pp. 19–63 {{ZBL|0695.26007}}</td></tr> | ||
| + | <tr><td valign="top">[a3]</td> <td valign="top"> F. Neuman, "Factorizations of matrices and functions of two variables" ''Czech. Math. J.'' , '''32''' : 107 (1982) pp. 582–588</td></tr> | ||
| + | <tr><td valign="top">[a4]</td> <td valign="top"> F. Neuman, "Functions of two variables and matrices involving factorizations" ''C.R. Math. Rept. Acad. Sci. Canada'' , '''3''' (1981) pp. 7–11</td></tr> | ||
| + | <tr><td valign="top">[a5]</td> <td valign="top"> F. Neuman, Th. Rassias, "Functions decomposable into finite sums of products" , ''Constantin Catathéodory–An Internat. Tribute'' , '''II''' , World Sci. (1991) pp. 956–963</td></tr> | ||
| + | <tr><td valign="top">[a6]</td> <td valign="top"> C.M. Stéphanos, "Sur une categorie d'équations fonctionalles" , ''Math. Kongr. Heidelberg'' , '''1905''' (1904) pp. 200–201</td></tr> | ||
| + | <tr><td valign="top">[a7]</td> <td valign="top"> C.M. Stéphanos, "Sur une categorie d'équations fonctionalles" ''Rend. Circ. Mat. Palermo'' , '''18''' (1904) pp. 360–362</td></tr> | ||
| + | <tr><td valign="top">[a8]</td> <td valign="top"> Th.M. Rassias, J. Šimša, "Finite sum decompositions in mathematical analysis" , Wiley (1995)</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> Th.M. Rassias, J. Šimša, "19 Remark" ''Aequat. Math.'' , '''56''' (1998) pp. 310</td></tr> | ||
| + | </table> | ||
Latest revision as of 12:53, 22 March 2023
Consider the decomposition of a function $h ( x , y )$ into a finite sum of the form
\begin{equation*} h ( x , y ) = \sum _ { k = 1 } ^ { n } f _ { k } ( x ) g _ { k } ( y ). \end{equation*}
For sufficiently smooth $h$, a necessary condition for such a decomposition involves determinants of the form
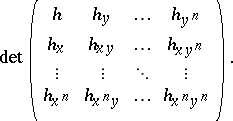 |
These determinants were introduced in [a6] and [a7], and a correct formulation of the sufficient condition was given in [a3]; see also [a4].
A sufficient and necessary condition for not sufficiently smooth functions $h ( x , y )$ defined on arbitrary (even discrete) sets without any regularity conditions was formulated in [a3], [a4] by introducing a new, special matrix
\begin{equation*} \left( \begin{array} { c c c c } { h ( x _ { 1 } , y _ { 1 } ) } & { h ( x _ { 1 } , y _ { 2 } ) } & { \dots } & { h ( x _ { 1 } , y _ { n } ) } \\ { h ( x _ { 2 } , y _ { 1 } ) } & { h ( x _ { 2 } , y _ { 2 } ) } & { \dots } & { h ( x _ { 2 } , y _ { n } ) } \\ { \vdots } & { \vdots } & { \ddots } & { \vdots } \\ { h ( x _ { n } , y _ { 1 } ) } & { h ( x _ { n } , y _ { 2 } ) } & { \dots } & { h ( x _ { n } , y _ { n } ) } \end{array} \right); \end{equation*}
Several authors have dealt with problems concerning decompositions of functions of several variables and similar questions, see, e.g., [a1], [a2], [a8]. However, several open problems in this area remain (as of 2000), e.g.: find a characterization of functions $h ( x , y )$ of the form
\begin{equation*} h ( x , y ) = F ( \sum _ { k = 1 } ^ { n } f _ { k } ( x ) . g _ { k } ( y ) ), \end{equation*}
see [a5].
References
| [a1] | M. Čadek, J. Šimša, "Decomposable functions of several variables" Aequat. Math. , 40 (1990) pp. 8–25 |
| [a2] | H. Gauchman, L.A. Rubel, "Sums of products of functions of $x$ times functions of $y$" Linear Alg. & Its Appl. , 125 (1989) pp. 19–63 Zbl 0695.26007 |
| [a3] | F. Neuman, "Factorizations of matrices and functions of two variables" Czech. Math. J. , 32 : 107 (1982) pp. 582–588 |
| [a4] | F. Neuman, "Functions of two variables and matrices involving factorizations" C.R. Math. Rept. Acad. Sci. Canada , 3 (1981) pp. 7–11 |
| [a5] | F. Neuman, Th. Rassias, "Functions decomposable into finite sums of products" , Constantin Catathéodory–An Internat. Tribute , II , World Sci. (1991) pp. 956–963 |
| [a6] | C.M. Stéphanos, "Sur une categorie d'équations fonctionalles" , Math. Kongr. Heidelberg , 1905 (1904) pp. 200–201 |
| [a7] | C.M. Stéphanos, "Sur une categorie d'équations fonctionalles" Rend. Circ. Mat. Palermo , 18 (1904) pp. 360–362 |
| [a8] | Th.M. Rassias, J. Šimša, "Finite sum decompositions in mathematical analysis" , Wiley (1995) |
| [a9] | Th.M. Rassias, J. Šimša, "19 Remark" Aequat. Math. , 56 (1998) pp. 310 |
D'Alembert equation for finite sum decompositions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=D%27Alembert_equation_for_finite_sum_decompositions&oldid=50464