Difference between revisions of "Lituus"
From Encyclopedia of Mathematics
(TeX) |
(svg picture) |
||
| Line 4: | Line 4: | ||
$$\rho=\frac{a}{\sqrt\phi}.$$ | $$\rho=\frac{a}{\sqrt\phi}.$$ | ||
| − | + | [[File:Lituus.svg|center|400px|Lituus]] | |
| − | |||
| − | |||
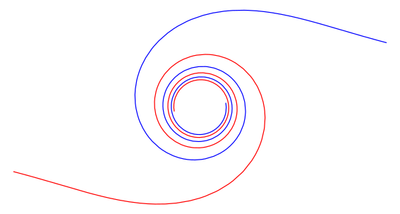
To every value of $\phi$ correspond two values of $\rho$, one positive and one negative. The curve consists of two branches, that both approach the pole asymptotically (see Fig.). The line $\phi=0,\phi=\pi$ is an asymptote at $\rho=\pm\infty$, and $(1/2,a\sqrt2)$ and $(-1/2,-a\sqrt2)$ are points of inflection. The lituus is related to the so-called algebraic [[Spirals|spirals]]. | To every value of $\phi$ correspond two values of $\rho$, one positive and one negative. The curve consists of two branches, that both approach the pole asymptotically (see Fig.). The line $\phi=0,\phi=\pi$ is an asymptote at $\rho=\pm\infty$, and $(1/2,a\sqrt2)$ and $(-1/2,-a\sqrt2)$ are points of inflection. The lituus is related to the so-called algebraic [[Spirals|spirals]]. | ||
====References==== | ====References==== | ||
| − | + | * {{Ref|1}} A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> F. Gomes Teixeira, "Traité des courbes" , '''1–3''' , Chelsea, reprint (1971)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> F. Gomes Teixeira, "Traité des courbes" , '''1–3''' , Chelsea, reprint (1971)</TD></TR></table> | ||
Latest revision as of 19:32, 16 March 2023
A plane transcendental curve whose equation in polar coordinates is
$$\rho=\frac{a}{\sqrt\phi}.$$
To every value of $\phi$ correspond two values of $\rho$, one positive and one negative. The curve consists of two branches, that both approach the pole asymptotically (see Fig.). The line $\phi=0,\phi=\pi$ is an asymptote at $\rho=\pm\infty$, and $(1/2,a\sqrt2)$ and $(-1/2,-a\sqrt2)$ are points of inflection. The lituus is related to the so-called algebraic spirals.
References
- [1] A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)
References
| [a1] | K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
How to Cite This Entry:
Lituus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lituus&oldid=32535
Lituus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lituus&oldid=32535
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article