Difference between revisions of "Galilean spiral"
From Encyclopedia of Mathematics
(Importing text file) |
(svg picture) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A plane curve whose equation in polar coordinates is | A plane curve whose equation in polar coordinates is | ||
| − | + | $$\rho=a\phi^2-l,\quad l\geq0.$$ | |
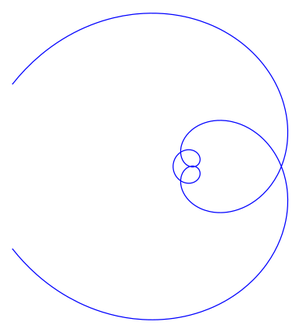
| − | The spiral is symmetric with respect to the polar axis (see Fig.) and has a double point at the pole with tangents forming angles equal to | + | The spiral is symmetric with respect to the polar axis (see Fig.) and has a double point at the pole with tangents forming angles equal to $\pm\sqrt{l/a}$ with the polar axis. |
| − | + | [[File:Galilean spiral.svg|center|300px|Galilean spiral with parameters (a,l)=(1,8)]] | |
| − | + | The polar axis of a Galilean spiral contains infinitely many double points, for which $\rho=ak^2\pi^2-l$, where $k=1,2,\ldots$. The Galilean spiral is a so-called algebraic spiral (cf. [[Spirals|Spirals]]). Named after G. Galilei (1683) in connection with his studies on the free fall of solids. | |
| − | |||
| − | The polar axis of a Galilean spiral contains infinitely many double points, for which | ||
====References==== | ====References==== | ||
| − | + | * {{Ref|1}} A.A. Savelov, "Planar curves", Moscow (1960) (In Russian) | |
Latest revision as of 19:26, 16 March 2023
A plane curve whose equation in polar coordinates is
$$\rho=a\phi^2-l,\quad l\geq0.$$
The spiral is symmetric with respect to the polar axis (see Fig.) and has a double point at the pole with tangents forming angles equal to $\pm\sqrt{l/a}$ with the polar axis.
The polar axis of a Galilean spiral contains infinitely many double points, for which $\rho=ak^2\pi^2-l$, where $k=1,2,\ldots$. The Galilean spiral is a so-called algebraic spiral (cf. Spirals). Named after G. Galilei (1683) in connection with his studies on the free fall of solids.
References
- [1] A.A. Savelov, "Planar curves", Moscow (1960) (In Russian)
How to Cite This Entry:
Galilean spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galilean_spiral&oldid=13942
Galilean spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galilean_spiral&oldid=13942
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article