Difference between revisions of "Petersen graph"
(tex done) |
|||
| Line 10: | Line 10: | ||
====References==== | ====References==== | ||
<table><tr><td valign="top">[a1]</td> <td valign="top"> D. Holton, J. Sheehan, "The Petersen graph" ''Austral. Math. Soc. Lecture Ser., CLT'' , '''7''' (1993)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> P.G. Tait, "Remarks on the colouring of maps" ''Proc. R. Soc. Edinburgh'' , '''10''' (1878-80) pp. 729</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> W.T. Tutte, "On the algebraic theory of graph colourings" ''J. Combin. Th.'' , '''1''' (1966) pp. 15–50</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> W.T. Tutte, "Colouring problems" ''Math. Intelligencer'' , '''1''' (1978) pp. 72–75</td></tr></table> | <table><tr><td valign="top">[a1]</td> <td valign="top"> D. Holton, J. Sheehan, "The Petersen graph" ''Austral. Math. Soc. Lecture Ser., CLT'' , '''7''' (1993)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> P.G. Tait, "Remarks on the colouring of maps" ''Proc. R. Soc. Edinburgh'' , '''10''' (1878-80) pp. 729</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> W.T. Tutte, "On the algebraic theory of graph colourings" ''J. Combin. Th.'' , '''1''' (1966) pp. 15–50</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> W.T. Tutte, "Colouring problems" ''Math. Intelligencer'' , '''1''' (1978) pp. 72–75</td></tr></table> | ||
| + | |||
| + | [[Category:Graph theory]] | ||
Revision as of 19:41, 15 March 2023
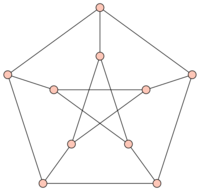
A graph that has fascinated graph theorists over the years because of its appearance as a counterexample in so many areas of the subject:
The Petersen graph is cubic, $3$-connected and has $10$ vertices and $15$ edges. There are exactly $19$ connected cubic graphs on $10$ vertices. The number of elements in the set $C ( n )$ of connected cubic graphs on $n$ vertices grows rapidly with $n$; for example, $| C ( 20 ) | = 510489$, $| C ( 30 ) | = 845480228069$. The Petersen graph is the only graph in $C ( 10 )$ with $120$ automorphisms (cf. also Graph automorphism); the only graph in $C ( 10 )$ with girth $5$; the only graph in $C ( 10 )$ with diameter $2$; the only bridgeless graph in $C ( 10 )$ with chromatic index $4$ (cf. also Graph colouring) and, finally, it is the only bridgeless non-Hamiltonian graph in $C( 10 )$.
Typically, however, the importance of the Petersen graph is the way it features as the exceptional graph. It is at least arguable that the development of graph theory was in large extent due to the interest in the four-colour problem. P.G. Tait [a2] showed that every planar graph is $4$-face colourable if and only if every bridgeless cubic planar graph is $3$-edge colourable, that is, if its chromatic index is at most $3$. W.T. Tutte [a3] conjectured that if $G$ is a bridgeless cubic graph with chromatic index at least $4$, then $G$ is subcontractible to the Petersen graph. Thus, even with the proof of the four-colour theorem there is much to prove beyond the theorem [a4] and typically the Petersen graph features prominently. In the same vein, W.T. Tutte [a3] conjectured that if $G$ is a bridgeless graph which does not support a nowhere-zero $4$-flow, then $G$ is subcontractible to the Petersen graph: the four-colour theorem guarantees that every bridgeless planar graph supports a nowhere-zero $4$-flow. Let $\overset{\rightharpoonup}{ G }$ be any orientation of the edges $E ( G )$ of $G$. A nowhere-zero $4$-flow on a graph $G$ is a mapping $f : E ( \vec { G } ) \rightarrow \mathbf{Z} _ { 4 } ^ { * }$ such that at each vertex $v$, $\sum f ( \overset{\rightharpoonup } { e } ) = 0$, where the summation is over all oriented edges $\overset{\rightharpoonup} { e }$ incident with $v$.
References
| [a1] | D. Holton, J. Sheehan, "The Petersen graph" Austral. Math. Soc. Lecture Ser., CLT , 7 (1993) |
| [a2] | P.G. Tait, "Remarks on the colouring of maps" Proc. R. Soc. Edinburgh , 10 (1878-80) pp. 729 |
| [a3] | W.T. Tutte, "On the algebraic theory of graph colourings" J. Combin. Th. , 1 (1966) pp. 15–50 |
| [a4] | W.T. Tutte, "Colouring problems" Math. Intelligencer , 1 (1978) pp. 72–75 |
Petersen graph. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Petersen_graph&oldid=52539